Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975

(19.75)

Наконец, для q'(а, х°) будем иметь

С учетом значений соответствующих синусов получим

(19.76)

Релейная характеристика с гистерезисной петлей. Считая, что релейная характеристика с гистерезисной петлей (рис. 19.10, в) есть частный случай релейной характеристики общего вида при m=-1, получим

(19.77) при а>b+|x° |.

Релейная характеристика с зоной нечувствительности. Релейную характеристику с зоной нечувствительности (рис. 19.10, г) следует рассматривать как частный случай релейной характеристики общего вида при m = 1. Тогда получим значения, постоянной составляющей и коэффициентов гармонической линеаризации:

(19.78) при а>b+|x° |.

Идеальная релейная характеристика. Для идеальной релейной характеристики (рис. 19.6, б), полагая в последних формулах b = 0, получим

(19.79) при а >|x0|.

Релейная несимметричная характеристика. Релейная несимметричная характеристика при гармоническом изменении входной величины х со смещенным

центром колебаний представлена на рис. 19.11, а. Так будет изменяться напряжение на потребителе, управляемом поляризованным реле, если реле при срабатывании включает потребитель на полное напряжение, а при отпускании выключает.

Вычисляя постоянную составляющую по формуле (19.6), получим

После подстановки значений соответствующих углов имеем

(19.80)

Далее,

или, с учетом значений углов ψ 1 и ψ 2,

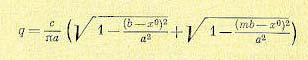(19.81) при а>|b-x0| и a>|x0-mb|.

Наконец,

или, с учетом соответствующих синусов,

(19.82)

при тех же ограничениях.

Нелинейная характеристика с зоной нечувствительности. Нелинейная характеристика с зоной нечувствительности изображена на рис. 19.12, а. Коэффициент q' в этом случае равен нулю, так как характеристика однозначная.

Определим значения постоянной составляющей F° (а, х°) и коэффициента гармонической линеаризации q(а, х°) в соответствии с видом функции F(х° + а sinψ ), показанной на рис.

19.12, б.

Для постоянной составляющей имеем

что после подстановки соответствующих углов дает

(19.83) при a>b+|x0|

Вычисляя коэффициент q(а, х0), получаем

что с учетом значений углов дает

(19.84) при а>b+|x0|;

Нелинейная характеристика с насыщением. Для нелинейной характеристики с насыщением (рис. 19.8) при несимметричных колебаниях аналогичным путем получаем следующие значения постоянной составляющей F0(а, х°) и коэффициента гармонической линеаризации q(а, х°):

(19.85) и представленные на рис. 19.13.

Из графиков для F° (рис. 19.13, а) видно, что при наличии колебаний входной величины нелинейного звена его статическая характеристика для медленно меняющегося

воздействия (функция смещения) сглаживается, причем увеличение амплитуды колебаний входной величины приводит к уменьшению коэффициента усиления нелинейного звена по постоянному или медленно меняющемуся входному воздействию.

Графики для q (рис. 19.13, 6) характеризуют прохождение через нелинейное звено колебательной составляющей в зависимости от амплитуды на входе и смещения центра

колебаний. Как видно, увеличение смещения приводит к уменьшению коэффициента усиления для колебательной составляющей.

Нелинейная характеристика типа люфта или зазора. В случае несимметричных колебаний нелинейная характеристика типа люфта или зазора (рис. 19.14) смещается вдоль средней линии, так что ее прежний центр 0 переходит в положение 0'. Постоянная составляющая в этом случае определяется простой формулой

Колебательная составляющая функции F(х° + а sinψ ) относительно нового центра

колебаний не зависит от величины смещения х°. Так, например, шестереночная пара, имеющая люфт, передает движение с тем же передаточным числом для любых углов поворота ведущей шестерни. В случае колебаний в кинематической передаче,

включающей данную шестереночную пару, люфт будет проявлять себя одинаково для любых углов поворота. Поэтому для коэффициентов гармонической линеаризации характеристики типа люфта или зазора в случае смещенного центра колебаний относительно начала отсчета будем иметь те же формулы (18.27), что и для случая симметричных колебаний.

ГЛАВА 20 ОЦЕНКА КАЧЕСТВА НЕЛИНЕЙНЫХ ПРОЦЕССОВ РЕГУЛИРОВАНИЯ

§ 20.1. Приближенное исследование колебательных переходных процессов

Рассмотрим симметричные относительно оси времени колебательные переходные процессы в нелинейной автоматической системе, которые в первом грубом приближении могут быть описаны затухающей или расходящейся синусоидой с медленно меняющимися во времени показателем затухания и частотой (рис. 20.1).

Прежде чем записать это математически, обратим внимание на два существенных обстоятельства. Для линейных систем, когда показатель затухания ξ = const и частота

w=const, пишут

(20.1)

Если же частота w и показатель затухания ξ , в процессе колебаний меняются с течением времени, то решение следует записывать в другом виде.

Во-первых, следует писать sinψ (t) и определять текущее значение частоты в произвольный момент времени в виде

(20.2)

Причем

(20.3)

где ψ 0— постоянная (начальная фаза). Существует другой способ, когда

полагаютψ =w0t+ϕ (t) при w0=const, причем согласно (20.2) текущее значение частоты

(20.4)

Однако в данной задаче целесообразно придерживаться первого представления (20.2) и (20.3)

Во-вторых, при переменном во времени показателе затухания следует определять текущее значение амплитуды а (рис. 20.1) не в виде a0 eξt , как сделано в (20.1), а в виде дифференциальной зависимости

Здесь в общем случае коэффициенты гармонической линеаризации будут зависеть от трех неизвестных: a, w и ξ . Если же рассматривается нелинейность F(х), как чаще всего

бывает, то q и q' сохраняют прежний вид:

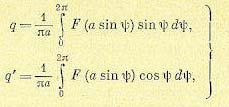(20.14)

и в этом случае можно целиком использовать материал главы 18 в виде готовых выражений q(а) и q'(а) для различных конкретных нелинейностей, учитывая, однако, новую форму (20.12) замены нелинейной функции.

В случае нелинейных систем первого класса дифференциальное уравнение колебательного переходного процесса

(20.15)

при наличии свойства фильтра (§ 18.2) после гармонической линеаризации согласно (20.12) принимает вид

(20.16)

Колебательный процесс в линейной системе, описываемый решением (20.1), соответствует паре комплексных корней характеристического уравнения р = ξ + jw с

постоянными значениями ξ и w. Аналогично и колебательный процесс в нелинейной

системе, описываемый приближенно формулами (20.7) и (20.8), определяется медленно меняющимися значениями ^ и со, которые можно находить путем определения пары комплексных корней р = ξ ± jw характеристического уравнения гармонически

линеаризованной системы (20.16).

В соответствии с этим в характеристическое уравнение

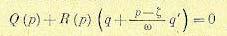(20.17)

подставим р =ξ +jw для определения значений ξ и w, удовлетворяющих этому уравнению. В результате получим

(20.18)

Подстановку значения ξ + jw вместо р в любой многочлен удобно выполнять путем разложения его в ряд по степеням jw, например;

где индекс ξ означает, что в выражения производных надо подставить ξ вместо р. По такой же формуле разлагается в ряд и многочлен R(ξ + jw). При малых значениях ξ (для

медленно затухающих процессов) вместо (20.19) удобнее применять разложение по степеням ξ , ограничиваясь его первой степенью, а именно:

где индекс jw означает подстановку jw вместо p в выражения для производных. В комплексном уравнении (20.18) содержатся три неизвестные: ξ , w и а, причем

последняя входит в q и q'. Поэтому указанное комплексное уравнение позволяет найти две переменные как функцию третьей: