
Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975
.pdf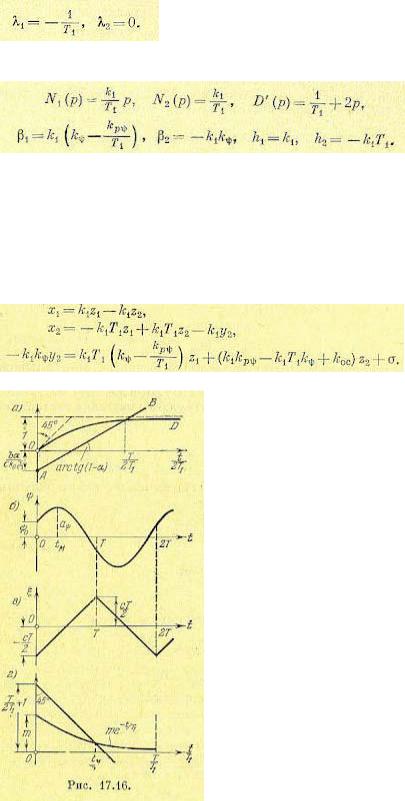
Вычислив N1(р) и N2(p) согласно указанию формуле (17.83), а также производную D' (р) и коэффициенты β 1; β 2, h1, h2 по формулам (17.87) и (17.92), получим:
В результате канонические уравнения (17.89) здесь будут
 (17.103)
(17.103)
а выражения (17.91) для прежних переменных x1, x2, ξ через канонические z1 и z2 Примут вид
Подставив y2 из последнего уравнения во второе и использовав (17.102), получаем
следующие выражения для исходных переменных через канонические:
 (17.104)
(17.104)
Далее согласно (17.97) записываем уравнения для определения полупериода автоколебаний:

или
 (17.105)
(17.105)
где введено обозначение
 (17.106)
(17.106)
Левая часть равенства (17.105) изображается прямой АВ (рис. 17.16,а), а правая Рис. 17.16. часть — кривой OD. Точка пересечения их является решением уравнения (17.105). Из графика видно, что это уравнение имеет решение только при условии
 (17.107)
(17.107)
причем
При а > 1 прямая АВ не пересекается с кривой ОD, что означает отсутствие автоколебаний при этих значениях а.
Но кроме равенства (17.105) необходимо еще выполнение условия переключения (17.98), которое в данном случае будет
или
 (17.108)
(17.108)
Следовательно, если даже значение, а лежит в интервале (17.107), но не выполняется условие (17.108), то автоколебаний в системе не будет.
Для исследования устойчивости автоколебаний запишем характеристическое уравнение (17.100). Оно получает здесь вид
Случай 1 + pth 2TT1 = 0 , когда знаменатель обращается в нуль, нереален. Поэтому, считая
1 + pth 2TT1 ≠ 0 , приведем это уравнение к общему знаменателю, использовав обозначение
(17.106), что дает
Поскольку данное характеристическое уравнение имеет вторую степень, то для устойчивости исследуемых колебаний необходима и достаточна положительность его коэффициентов. Коэффициент при р2 положителен. Коэффициент при р согласно (17.107) тоже положителен. Поэтому условие устойчивости автоколебаний сводится к положительности свободного члена этого уравнения, т. е.
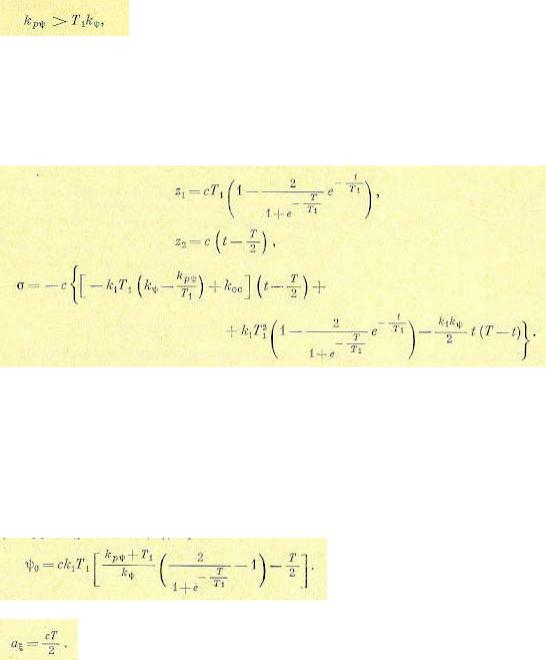

Амплитуда автоколебаний самолета (по углу рыскания) aψ найдется как максимум функции ψ (t) на участке 0 < t< Т. Взяв от ψ (17.112) производную по t и приравняв ее
нулю, получаем следующее уравнение для определения времени t= tм, соответствующего максимуму ψ :
Это уравнение решается графически, как показано на рис. 17.16, г. Определив таким образом величину tм, подставляем ее в первую из формул (17.112), что и дает искомую амплитуду автоколебаний самолета
Частота же автоколебаний определяется через полупериод Т, найденный на основании уравнения (17.105) графически (рис. 17.16, а).
Заметим, что задача в данном примере ради простоты решена лишь для упрощенного уравнения движения самолета по курсу (первое из уравнений (17.101)) и в предположении строгого постоянства скорости рулевой машинки.
§ 17.4. Частотный метод В. М. Попова
Решение задачи об абсолютной устойчивости системы с одной однозначной нелинейностью (т. е. устойчивости при любой форме этой нелинейности со слабым ограничением типа (17.54) или типа рис. 17.14) с помощью теорем прямого метода Ляпунова было проиллюстрировано на двух примерах в § 17.2.
Изложим теперь частотный метод, предложенный румынским ученым В. М. Поповым [97], при использовании которого та же задача решается более просто приемами, аналогичными частотным способам исследования устойчивости линейных систем. Если в системе автоматического регулирования имеется лишь одна однозначная нелинейность
 (17.113)
(17.113)
то, объединив вместе все остальные (линейные) уравнения системы, можно всегда получить общее уравнение линейной части системы (рис. 17.17, а) в виде
 (17.114)
(17.114)
где

причем будем считать m< n.
Пусть нелинейность у = F(х) имеет любое •очертание, не выходящее за пределы заданного угла arctgk (рис. 17.17, б), т. е. при любом x
 (17.115)
(17.115)
Пусть многочлен Q(р) или, что то же, характеристическое уравнение линейной части Q(р)= 0 имеет все корни с отрицательными вещественными частями или же кроме них имеется еще не более двух нулевых корней. Другими словами, допускается, чтобы аn = 0 или аn = 0 и аn-1 = 0 в выражении Q(р), т. е. не более двух нулевых полюсов в передаточной функции линейной части системы
Приведем без доказательства формулировку теоремы В. М. Попова: для установления устойчивости нелинейной системы достаточно подобрать такое конечное действительное число И, при котором при всех w ≥0
 (17.116)
(17.116)
где W(jw) — амплитудно-фазовая частотная, характеристика линейной части системы. При наличии одного нулевого полюса требуется еще, чтобы
а при двух нулевых полюсах
Теорема справедлива также и при наличии в знаменателе Q(р) передаточной функции линейной части не более двух чисто мнимых корней, но при этом требуются некоторые другие простые добавочные условия [2], называемые условиями предельной устойчивости.
Другая формулировка той же теоремы, дающая удобную графическую интерпретацию, связана с введением видоизмененной частотной характеристики W* (jw), которая определяется следующим образом:
где То = 1 сек — нормирующий множитель.
График W* (jw) имеет вид (рис. 17.18, а), аналогичный W(jw), когда в выражениях Q(р) и
R(р) разность степеней n-m > 1 . Если же разность степеней n-m = 1, то конец графика W* (jw) будет на мнимой оси ниже начала координат (рис. 17.18, б).
Преобразуем левую часть неравенства (17.116):

Тогда, положив
и использовав соотношения (17.117), получим вместо (17.116) для теоремы В. М. Попова условие
 (17.118).
(17.118).
при всех w>0 Очевидно, что равенство
 (17.119)
(17.119)
представляет уравнение прямой на плоскости W* (jw).
Отсюда вытекает следующая графическая интерпретация теоремы В. М. Попова: для установления устойчивости нелинейной системы достаточно подобрать такую прямую на плоскости W* (jw), проходящую через точку (-1/k ,j0), чтобы вся кривая W* (jw) лежала справа от этой прямой.
На рис. 17.19 показаны случаи выполнения теоремы. В этих случаях нелинейная система устойчива при любой форме однозначной нелинейности, ограниченной лишь условием (17.115). На рис. 17.20 показаны случаи, когда теорема не выполняется, т.е. нелинейная система не имеет абсолютной устойчивости.
Заметим, что, например, в задаче о самолете с автопилотом (§ 17.2) условие (17.54) означает любое расположение нелинейной характеристики во всем первом (и третьем) квадранте. Во всех подобных случаях согласно рис. 17.17 имеем Н = оо. В теореме В. М. Попова при этом вместо (17.116) получаем условие
 (17.120) а вместо (17.118)
(17.120) а вместо (17.118)
 (17.121)
(17.121)
при всех w > 0. Поэтому в графической интерпретации прямая должна проходить не так, как показано было на рис. 17.19, а через начало координат. В частности, для указанного примера (§ 17.2) уравнения (17.63) можно преобразовать к виду

где обозначено у= -рх2, причем р — производная по τ . Передаточная функция линейной части системы будет
Отсюда
Умножив числитель и знаменатель на 1-jw, получим
а согласно (17.117)
 (17.122)
(17.122)
Неравенство (17.121) принимает вид
 (17.123)
(17.123)
Очевидно, что это неравенство может быть выполнено при любом w>0 если
 (17.124)
(17.124)
и если h берется сколь угодно большим, чтобы обеспечить неравенство (17.123) при сколь угодно малых w.
Полученное условие (17.124) выполняется при
что точно совпадает с найденными ранее условиями абсолютной устойчивости данной системы (17.69) и (17.70). Смысл практической реализации этих условий был разъяснен в
§ 17.2.
Графически критерий устойчивости выражается в том, что вся кривая W*(jw) = U*(jw)+jV*(w), построенная согласно (17.122), расположена (рис. 17.21, а) справа от прямой U* — hV* =0, обозначенной штрих-пунктиром, со сколь угодно малым наклоном, если 1+r-γ > 0. Если же 1+r -γ < 0 (рис. 17.21, б), то такую прямую провести невозможно
и, следовательно, нелинейная система не будет абсолютно устойчивой.
Здесь был приведен простой пример, в котором условия устойчивости по методу В. М. Попова выражаются в общем буквенном виде. В большинстве технических задач этого не
получится. Однако видно, что описанный частотный критерий устойчивости В. М. Попова для систем с одной однозначной нелинейностью в его графической форме может быть применен при любой сложности линейной части системы и численно заданных коэффициентах уравнений. Более того, он может быть применен в случае, когда не заданы уравнения, но известна экспериментально снятая амплитудно-фазовая частотная характеристика линейной части W(jw). Чтобы установить устойчивость системы согласно рис. 17.19, W(jw) надо перестроить в характеристику W*(jw), пользуясь формулами
(17.117).
Очертание нелинейности может быть неизвестным. Необходимо знать лишь, в пределах какого угла (рис. 17.17) она расположена. Для конкретно заданных форм нелинейности область устойчивости, вообще говоря, будет несколько шире, но данным методом это не определяется (см. главу 18).
§ 17.5. Исследование систем с переменной структурой
Понятие о системах с переменной структурой было дано в начале книги (§2.3), а об их уравнениях — в конце главы 16.
Покажем методику исследования систем с переменной структурой при отсутствии внешнего воздействия на примере системы второго порядка при линейном объекте и линейных структурах регулятора, так что нелинейность системы будет заключаться в автоматическом переключении этих структур.
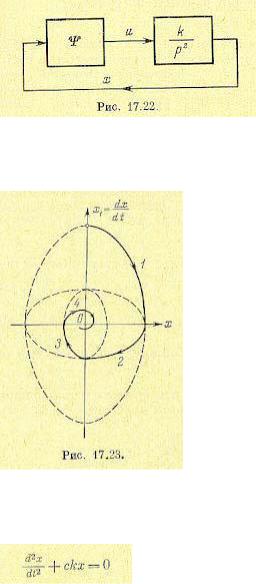
Имея в виду второй порядок системы, используем изображение процессов на фазовой плоскости, которое для линейных систем представлено было выше на рис. 16.8—16.13. Рассмотрим систему (рис. 17.22), не обладающую при постоянной структуре собственной устойчивостью [42]. В самом деле, если Ψ = const , то уравнение системы будет
и получатся незатухающие колебания, изображаемые на фазовой плоскости концентрическими эллипсами (рис. 16.8).

Если же звену Ψ придать вид, как на рис. 16.27, а, где x1 = dxxt с переключением согласно формуле (16.71), где α = k1 получим уравнения системы
 (17.125)
(17.125)
 (17.126)
(17.126)
Первое из них будет действовать в первом и третьем квадрантах фазовой плоскости (рис. 17.23), а второе — в четвертом и втором квадрантах. С эллипса 1 в первом квадранте (соответствует коэффициенту k1) изображающая точка переходит на эллипс 2 в четвертом квадранте (соответствует коэффициенту k2), затем на эллипс 3, концентрический с первым (снова коэффициент k1), далее на эллипс 4, концентрический с эллипсом 2, и т. д. В результате таких переключений система становится устойчивой.
В данном примере переходный процесс представляет собой затухающие колебания. В большинстве случаев для избежания колебательных процессов в системах с переменной структурой следует стремиться реализовать скользящий режим.
Для этого переключения в системе должны производиться в таких местах, где фазовые траектории направлены навстречу друг другу.
Покажем это на примере.
Пусть в той же системе (рис. 17.22) звено также устроено по принципу рис. 16.27, а, но
 (17.127)
(17.127)
Тогда прежнее выражение для Ψ
получает другой смысл. Возьмем при этом
Получим два уравнения системы:
 (17.128)
(17.128)
 (17.129)
(17.129)
Линиями раздела между областями их действия будут
т. е. ось ординат и наклонная прямая на фазовой плоскости (рис. 17.24). При этом уравнение (17.128) будет действовать в первом и третьем секторах фазовой плоскости. Поэтому там фазовыми траекториями будут служить согласно рис. 16.8 концентрические эллипсы. Уравнение же (17.129) будет действовать во втором и четвертом секторах фазовой плоскости (рис. 17.24), где фазовые траектории изобразятся в соответствии с рис. 16.3.
Обе эти линейные структуры (17.128) и (17.129) по отдельности не обладают устойчивостью. Благодаря же переключениям система в целом становится устойчивой. В отличие от предыдущей системы, здесь, как видно из рис. 17.24, нет колебательного процесса. При любых начальных условиях фазовая траектория приходит на наклонную прямую х1 = 0, где она встречается с фазовой траекторией с противоположным ей направлением движения. Поэтому переход изображающей точки через прямую х1= 0 невозможен. В результате изображающая точка вынуждена двигаться вдоль прямой х1= 0 в сторону начала координат, что и представляет собой скользящий режим переходного процесса в данной системе.
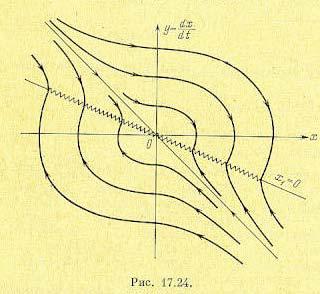
Практически скользящее движение будет сопровождаться вибрациями вследствие быстрых переключений то в одну, то в другую сторону, как и показано на рис. 17.24. Ввиду неидеальности системы (дополнительной инерционности или запаздывания) эти вибрации будут иметь конечные амплитуду и частоту. При идеальном же рассмотрении, проведенном выше, амплитуда их равна нулю, а частота — бесконечности. Рассмотрение реального переходного процесса скользящего типа с конечными вибрациями за счет дополнительной инерционности, повышающей порядок уравнения, возможно с помощью приближенного метода гармонической линеаризации. Это можно сделать аналогично рассмотрению медленно меняющихся сигналов в автоколебательных системах (§ 19.2), если за медленно меняющийся сигнал принять основное апериодическое движение в скользящем процессе, а наложенные на него вибрации рассчитать, как автоколебательную составляющую процесса (см. [101]).

 (17.109)
(17.109)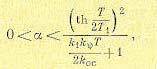 (17.110)
(17.110) (17.112)
(17.112)