
Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975
.pdf
возьмем z-преобразование от правой и левой частей
На основании (15.59) имеем, далее,
Отсюда можно найти изображение неполной суммы
 (15.64)
(15.64)
Распространяя эту зависимость на случай k-кратного суммирования можно записать
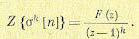 (16.65)
(16.65)
Для полной суммы (15.13) аналогичным образом можно найти первую обратную разность
ее изображение из (15.61)
Отсюда изображение полной суммы
 (15.66)
(15.66)
Для случая k-кратного суммирования
 (15.67)
(15.67)
Из приведенного рассмотрения вытекает справедливость равенства
 (15.68)
(15.68)
Таким образом, взятие прямой разности и взятие неполной суммы (или обратной разности и полной суммы) решетчатой функции являются обратными операциями. Роль оператора, аналогичного оператору р = с+jw в непрерывных системах, в первом случае играет
оператор (z — 1), а во втором случае — оператор z −z 1 . В случае перехода к пределу при
Т→ 0 обе пары операций над решетчатыми функциями сливаются и превращаются в операции дифференцирования и интегрирования непрерывных функций.
7. Изображения решетчатых функций с измененным периодом следования. Пусть рассматривается решетчатая функция с периодом следования дискрет λ Т, где λ ≠1. Тогда на основании (15.29) можно записать
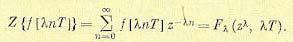 (15.69)
(15.69)
Из (15.69) следует, что при изменении периода в λ раз необходимо в изображении решетчатой функции f[n] заменить z на z λ и Т на λ Т. Так, например, если
рассматривается решетчатая функция e−anT , то при введении периода λ Т в соответствии с табл. 15.1 изображение будет
где z1 = z λ и d1 = d λ На рис. 15.8 построены для этого случая решетчатые функции с
исходным периодом следования Т (рис. 15.8, а), растянутым периодом при λ > 1 (рис. 15.8, б) и сжатым периодом при λ < 1 (рис. 15.8, в).

8. Сумма ординат решетчатой функции. Если абсцисса абсолютной сходимости решетчатой то, положив в (15.29) p = 0, имеем
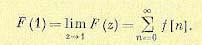 (15.70)
(15.70)
9. Конечное значение решетчатой функции. Составим первую прямую разность решетчатой функции f[n] и на основании (15.47) найдем ее изображение
Далее на основании (15.70) найдем сумму ординат ∆f[n]:
Кроме того, можно записать
Из двух последних выражений следует:
 (15.71)
(15.71)
Если провести аналогичное рассмотрение с первой обратной разностью, то можно получить формулу для вычисления конечного значения решетчатой функции в другом виде:
 (15.72)
(15.72)
10. Начальное значение решетчатой функции. Составим первую прямую разность и на основании (15.48) найдем ее изображение
Рассмотрим теперь предел выражения
Тогда из последних двух формул можно найти
(15.73)

Зависимости (15.72) и (15.73) представляют собой аналоги соответствующих выражений для нахождения конечного и начального значений непрерывной функции f(t) по ее изображению Лапласа:
11. Свертка решетчатых функций. Если
то можно показать, что
 (15.74)
(15.74)
Эта формула аналогична соответствующему выражению для свертки двух непрерывных функций.
12. Формула обращения. Рассмотрим задачу нахождения решетчатой функции (оригинала) по ее изображению. Эту операцию запишем в символическом виде как обратное z- преобразование:
 (15.75)
(15.75)
 (15.76)
(15.76)
Заметим, что аргумент изображения обладает свойством
 (15.77)
(15.77)
где k — произвольное целое число. Вследствие этого изображения F(z) и F(z, ε ) представляют собой периодическую функцию относительно мнимой части аргумента р=у+ jw с периодом 2πT , что дает основание рассматривать изображения только внутри интервала изменения 0 ≤ w < 2πT .
Удобнее использовать интервал — πT −1 < w ≤πT −1 так как он оказывается аналогичным интервалу частот − ∞ < w < ∞, рассматриваемому обычно для непрерывных функций времени. Принятый интервал дает на комплексной плоскости р =γ + jw область
(рис. 15.9), в которой достаточно рассматривать изображение F(z) = F(ерT).
Изображение F(z) может иметь в этой области особые точки тина полюсов — pi (где i = 1, 2, . . ., k). Полюсы могут быть или вещественными или комплексно сопряженными. В
случае |
p |
=γ |
1 |
± jπT −1 |
достаточно рассматривать один из этих полюсов, |
|
1,2 |
|
|
|
соответствующий, например, положительной мнимой части (на верхней границе области). Рассмотрим выражение (15.29):


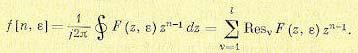 (15.85)
(15.85)
Полученные выражения (15.79), (15.80), (15.84) и (15.85) несколько сложны для практического использования. Поэтому для нахождения решетчатой функции по ее изображению обычно применяются другие методы, которые даны ниже.
13. Формулы разложения. Если изображение представляет собой простейшую табличную форму (см., например, табл. 15.1), то переход к оригиналу не представляет трудностей. Сложная дробно-рациональная форма может быть представлена в виде суммы дробей первой степени. Рассмотрим некоторые употребительные разновидности формулы разложения.
а) Пусть изображение F(z) представляет собой отношение двух многочленов:
причем будем предполагать, что степень числителя не выше, чем степень знаменателя, а корни знаменателя простые. Тогда изображение можно представить в виде суммы
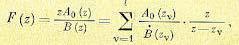 (15.86)
(15.86)
где В’(z) — производная В (z) по z, а zv (v= 1, 2, . . ., l) — корни знаменателя. Элементарному слагаемому z(z —zv)-1 соответствует оригинал e−av nT = zvn , где
av =T −1 ln zv−1 (см. табл. 15.1). В табл. 15.1 единственный корень дроби первой
степени обозначен z1 = d.
Поэтому оригинал (15.86) можно записать следующим образом:
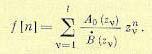 (15.87)
(15.87)
б) Пусть изображение F(z) не имеет нулевого корня числителя, но степень числителя А
(z) меньше степени знаменателя. Тогда, как следует из (15.73), начальное значение решетчатой функции f[0] = 0.
Для нахождения оригинала в этом случае можно воспользоваться формулами (15.86) и (15.87), но применить их следует для сдвинутой на один такт влево решетчатой функции, изображение которой будет zF(z). Для тога чтобы получить в результате искомую функцию, следует в правой части (15.87) сделать сдвиг на один такт вправо, для чего нужно заменить n на n — 1. В результате имеем
 (15.88)
(15.88)
причем последнее выражение будет справедливым только для n>1.
в) Пусть изображение F(z) не имеет нулевого корня числителя А (z), причем степень А(z) равна степени знаменателя В(z). Тогда следует понизить степень числителя, поделив его на знаменатель, и представить Р (г) в виде суммы составляющей нулевого порядка и дробно-рационального остатка F0 (z). В соответствии с формулой (15.29) первая составляющая равна начальному значению решетчатой функции f(0). Поэтому
Переход от второй составляющей изображения к оригиналу может быть сделан по формуле (15.88), которая справедлива для n> 1.


В случае, когда степень числителя F(z) равна степени знаменателя, следует аналогично изложенному выше выделить член нулевого порядка f[0] делением числителя на знаменатель и рассматривать далее остаток от деления.
14. Разложение в ряд Лорана. Из основного выражения для нахождения z-преобразования
(15.29) следует:
Разложив любым способом изображение F (z) , в ряд Лорана (ряд по убывающим степеням z);
и сравнивая два ряда между собой, можно установить, что с0 = f[0], с1 = f[1], с2 = f[2], . . .,
сk = f[k] и т. д.
Разложение в ряд можно делать любым способом, так как такое разложение единственно. Наиболее удобным приемом для дробно-рациональных функций является деление числителя на знаменатель.
Применяя разложение в ряд Лорана, можно вычислить значения оригинала f[n] или f[n, ε ] в дискретных точках без нахождения полюсов изображения F(z).
15. Решение разностных уравнений. Пусть имеется разностное уравнение в форме (15.15)
с начальными условиями у[v] = уv (v = 0, 1, . . ., m — 1). Найдем z-преобразование от его левой и правой частей. В соответствии с формулой (15.50) для случая упреждения на m тактов
Аналогичные зависимости могут быть записаны для упреждения на (m — 1), (m — 2), . . ., 1 тактов. Поэтому при переходе в рассматриваемом разностном уравнении к изображениям можно получить
 (15.93)
(15.93)
В правой части (15.93), кроме изображения F(z) решетчатой функции f[n], находятся члены, определяемые начальными условиями. Сумма их обозначена Уо (z).
Из (15.93) можно найти изображение У(z) искомой решетчатой функции
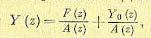 (15.94)
(15.94)
где
Далее можно использовать изложенные выше приемы перехода к искомому оригиналу у[n].
Для решения рассматриваемого разностного уравнения необходимо, как следует из изложенного, знать начальные условия у[v] = yv (V = 0, 1, . . ., m — 1). Последние же зависят от вида действующей в правой части разностного уравнения решетчатой функции. Более удобны для решения разностные уравнения вида (15.19)
с начальными условиями
Изображение решетчатой функции у [n — m], запаздывающей на т тактов, в соответствии с (15.48) будет
Подобные зависимости могут быть записаны для запаздывания на (m — 1), (m — 2), . . ., 1 тактов.
При переходе в рассматриваемом разностном уравнении к изображениям могут быть получены выражения, аналогичные (15.93) и (15.94). Переход к искомой решетчатой функции у [n] осуществляется в соответствии с изложенными выше приемами.
Особый интерес представляет случай, когда до момента времени n = 0 искомая решетчатая функция тождественно равна нулю. Это эквивалентно случаю нулевых начальных условий слева (при t = -0) при решении дифференциальных уравнений для непрерывных функций. Тогда в выражении для изображения (15.94) пропадает член в правой части, определяемый начальными условиями, и оно приобретает вид
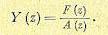 (15.95)
(15.95)
Рассмотрим разностное уравнение вида (15.19), но записанное в более общем виде:
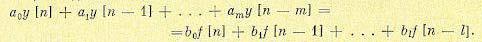 (15.96)
(15.96)
Если ввести предположение, что решетчатая функция у [n] тождественно равна нулю при n < 0 и, кроме того, функция f[n] в правой части (15.96) прикладывается в момент времени n= 0, то переход к изображениям дает
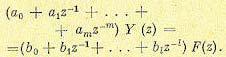 (15.97)
(15.97)
Изображение искомой решетчатой функции можно представить в виде
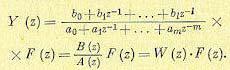 (15.98)
(15.98)
Здесь введена дискретная передаточная функция W(z), которая, как и в случае

Из последнего выражения следует, что при четном r будет сr = 0, т. е. четные гармоники отсутствуют. При r нечетном
 (15.110)
(15.110)
Если N нечетно, то при r = N
 (15.111)
(15.111)
Так как здесь присутствуют только нечетные гармоники, то тригонометрический ряд может быть записан в вещественной форме:
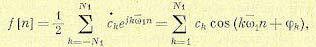 (15.112)
(15.112)
где N1 = N—1 для четных N и N1 = N для нечетных N.
Для нахождения изображения периодической решетчатой функции (15.99) применим теорему сдвига (15.50):
Отсюда следует:
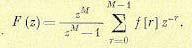 (15.113)
(15.113)
Сумма в правой части (15.113) представляет собой изображение решетчатой функции на интервале 0 — М.
Для симметричной периодической функции f[n] = -f [n + N] аналогичным образом можно получить
 (15.114)
(15.114)
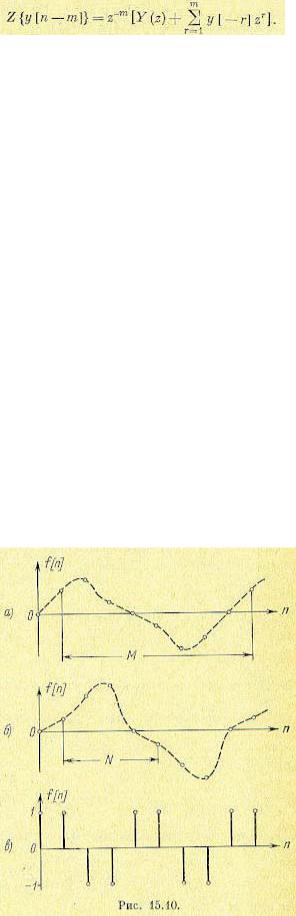
Найдем, например, изображение симметричной периодической решетчатой функции, показанной на рис. 15.10, в:
§ 15.3. Передаточные функции
Блочная схема импульсной системы, содержащая импульсный элемент ИЭ в канале ошибки, изображена на рис. 15.11. Импульсный элемент обычно считают идеальным. Понятие идеального импульсного элемента вводится двояким образом.
Можно положить, что идеальный импульсный элемент генерирует решетчатую функцию с периодом Т, образованную из непрерывного значения ошибки системы
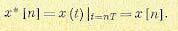 (15.115)
(15.115)
Здесь принято, что в решетчатой функции смещение ε = 0. Это всегда можно сделать выбором начала отсчета времени.

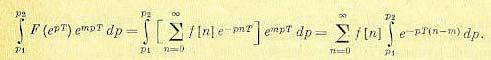 (15.78)
(15.78) (15.79)
(15.79)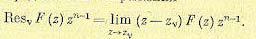 (15.81)
(15.81)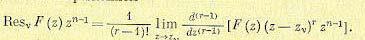 (15.82)
(15.82)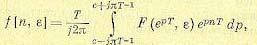 (15.84)
(15.84) (15.89)
(15.89)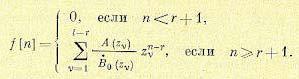 (15.90)
(15.90)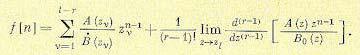 (15.91)
(15.91)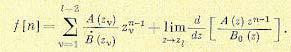 (15.92)
(15.92) (15.99)
(15.99)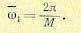 (15.100)
(15.100)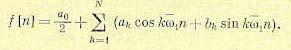 (15.101)
(15.101) (15.102)
(15.102) (15.103)
(15.103) (15.104)
(15.104) (15.105)
(15.105) (15.106) Для r = N при М =2N+1
(15.106) Для r = N при М =2N+1 (15.107)
(15.107)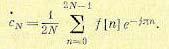 (15.108)
(15.108)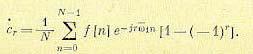 (15.109)
(15.109)