Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975

от синусоидального (18.173), будем для определения высших гармоник, порождаемых нелинейностью (т. е. на выходе нелинейного звена, где они не малые), подавать на вход нелинейного звена синусоиду (18.173).

Тогда каждая из высших гармоник на выходе нелинейного звена у = F(х, рх) в комплексной форме запишется в виде

(18.176)

где ak и β k— искомые амплитуда и фаза высшей гармоники уk на выходе нелинейного

звена, а — амплитуда входной синусоиды. При этом величины rk и sk определяются коэффициентами ряда Фурье, деленными на а, т. е.

(18.177)

Следовательно,

(18.178)

Затем эти немалые высшие гармоники с выхода нелинейного звена проходят через линейную часть (рис. 18.36) с передаточной функцией

становясь малыми за счет наличия свойства фильтра.

Учитывая перемену знака воздействия в замкнутой системе, получаем малые высшие гармоники для переменной х в виде (18.174), где

Окончательно находим:

(18.179)

или, в комплексной форме,

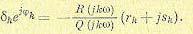(18.180)

Итак, по формулам (18.179) легко определяются относительная амплитуда и фаза каждой из высших гармоник (18.174) периодического решения (автоколебаний) для переменной х (18.175). Они вычисляются по известным амплитуде а и частоте w первого приближения (18.173), определению которого были посвящены предыдущие параграфы данной главы. Теперь произведем уточнение амплитуды а и частоты w первой гармоники за счет учета уже найденных высших гармоник. Уточненные значения а и w обозначаются через а1 и

w1.

Имея в виду форму решения (18.175), где х1 — первая гармоника, разложим нелинейную функцию Р (х, рх) в ряд Тейлор а;

Ограничимся написанными членами разложения ввиду малости высших гармоник

n

∑xk

k =2

Применяя далее разложение в ряд Фурье, по аналогии с § 18.1 получим

(18.181)

где имеем аналогичные прежним формулам первого приближения (18.7) основные коэффициенты (причем ψ = w1t )

(18.182)

и новые добавки к ним, вычисляемые, в отличие от этих основных, через первое приближение (18.173):

Они и дают уточнение первой гармоники х1 за счет учета высших гармоник искомого периодического решения. Формулы для ∆q и ∆q ' с учетом (18.174) можно преобразовать

к следующей, удобной для вычислений, форме;

(18.183)

где

(18.184)

причем

Подставив выражение (18.181) в уравнение системы (18.172) с учетом свойства фильтра, получим уравнение для определения уточненной первой гармоники х1 в виде

Характеристическое уравнение представим в форме

(18.185)

где введено обозначение

(18.186)

(замена w1 на w в малых добавках не играет существенной роли). Введение такого обозначения удобно по двум причинам. Во-первых, отделяются искомые а1 и w1, входящие в q и q', от известных величин ∆q и ∆q ', которые вычисляются здесь

предварительно по формулам (18.183) через найденные выше значения δk , ϕk и через а и

w, известные из первого приближения (§§ 18.1 — 18.4). Во-вторых, уравнение (18.185) для определения уточненной первой гармоники x1=a1sinw1t приведено к виду, формально совпадающему с уравнением (18.33), которое определяет первое приближение. Это позволяет использовать при определении уточненной первой гармоники совершенно те же способы, что и в § 18.2 для первого приближения. Кроме того, согласно (18.182) здесь можно использовать все прежние готовые выражения коэффициентов гармонической линеаризации q к q' для конкретно заданных нелинейностей с заменой только а, w на а1,

w1.

Итак, полностью найдено искомое уточненное решение для автоколебаний (18.175) в виде

Следует помнить, что, используя любой из способов § 18.2 применительно к данной задаче, надо везде вместо Q(р) ставить новый многочлен Q1 (р), отличающийся от Q(р) некоторыми добавками к его коэффициентам я определяемый по формуле (18.186). Важная особенность уточненного решения состоит еще и в том, что многочлен Q1(р), в отличие от прежнего Q(р), зависит не только от параметров линейной части системы, но, согласно (18.186) и (18.183), также т от формы нелинейности F (х, рх) за счет добавков ∆q

и ∆q '. Однако, в то время как основные коэффициенты q и q' имеют готовые выражения

для каждой нелинейности (см. § 18.1), здесь нельзя применять заранее вычисленные конкретные формулы для величин ∆q и ∆q ', так как входящие в формулы (18.183)

величины δk и ϕk , согласно (18.179), зависят от параметров и структуры линейной части

системы. Однако можно заранее вычислить для различных конкретных форм нелинейностей вспомогательные величины rk и sk .

О том, какой состав высших гармоник (18.175) в каждой конкретной задаче следует учесть, можно судить по разложению заданной нелинейной функции F(х, рх) в ряд Фурье. Так, например, в часто встречающемся на практике случае однозначной нечетносимметричной нелинейности F(х) наиболее существенной из высших гармоник будет третья. Учитывая ее, (представляем искомое периодическое решение (автоколебания), согласно (18.175), в виде

(18.187)

В этом случае в уравнении для первой гармоники (18.185), как и прежде, «будет равен нулю коэффициент q' и характеристическое уравнение будет

(18.188)

где

причем выражение для коэффициента

(18.189)

остается прежним (§ 18.1) с заменой а на a1. Формулы для добавочных коэффициентов ∆q и ∆q ' здесь значительно упрощаются, так как в формулах (18.183) и (18.184) многие

члены пропадают, а коэффициент sk= 0. В результате приходим к весьма простым соотношениям:

(18.190)

где введено новое сокращенное обозначение h3, причем

(18.191)

Из формул (18.179) определяются относительная амплитуда и фаза третьей гармоники:

(18.192)

Таким образом, достаточно просто определяется уточненное периодическое решение для случая однозначной нелинейности F(х) с учетом третьей гармоники в виде

(18.193)

Проведем вычисление коэффициентов h3 и r3 по формулам (18.191) для релейных характеристик, где оно представляет некоторые особенности.

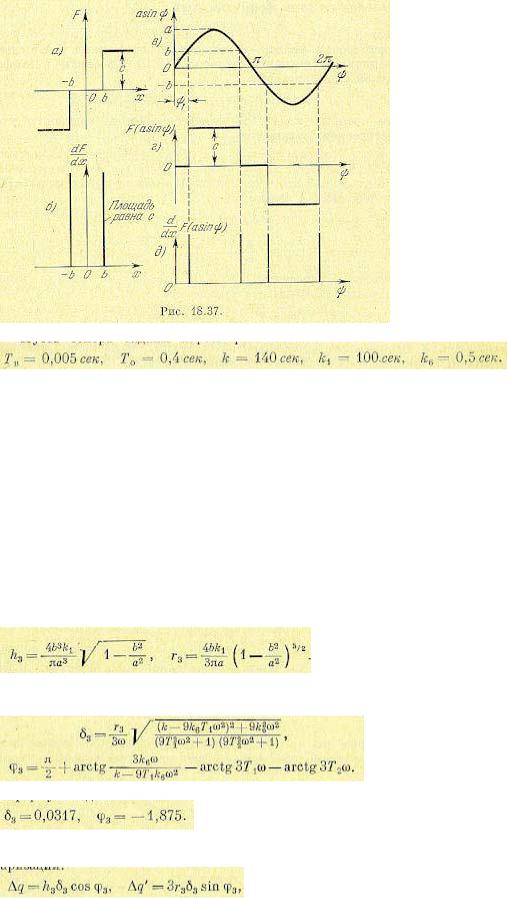
Рассмотрим релейную характеристику с зоной нечувствительности (рис. 18.37, а). Входящая под интеграл в формуле для h3 величина производной dF/dx будет для этой нелинейности равна нулю везде, кроме двух точек х = ±b, где она равна мгновенному импульсу, площадь которого равна с (рис. 18.37, б). Такой импульс называется дельтафункцией. Выражение sinψdψ при х =a sinψ можно преобразовать к виду

(18.194)

Поскольку подынтегральное выражение в формуле (18.191) для h3 на участке интегрирования (0, π /2) согласно рис. 18.37, д будет нулем везде, кроме одной точки ψ =ψ1 , то эту формулу в данном примере можно переписать в виде

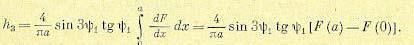(18.195)

а из рис. 18.37, а при a>b

Окончательно получаем

(18.196)

Формула (18.191) для r3 согласно рис. 18.37, г принимает вид

откуда с учетом соотношений (18.195) находим

(18.197)

В частности, для идеальной релейной характеристики из формул (18.196) и (18.197),

полагая b= 0, получим:

(18.198)

Рассмотрим два примера, иллюстрирующих процесс отыскания высших гармоник при автоколебаниях, а также уточнения первой гармоники за счет учета высших.

Пример 1. Исследуем следящую систему с нелинейностью типа насыщения, автоколебания в которой в первом приближении x=asinwt (уже были найдены ранее, в примере 1 § 18.3, в общем виде.

Пусть теперь заданы параметры системы:

Они удовлетворяют соотношению (18.76). Следовательно, здесь имеет место случай, изображенный на рис. 18.14, б, причем согласно (18.79) и (18.74) kв = 166 сек, kmin = 125 сек. Заданное значение k лежит между ними, что соответствует области наличия двух периодических режимов.

Выведенные выше формулы первого приближения (18.70) и (18.71) при это дают для неустойчивого режима а = 2,29 б, w = 118,2 сек-1, а для устойчивого режима а =21,4 в, w=44,8 сек-1, причем ам = 7,08 в (в точке wм рис. 18.14, б).

Наибольший интерес представляет первое (неустойчивое) периодическое решение. Оно указывает границу для начальных условий, вне которой переходный процесс в системе будет расходиться, стремясь к автоколебаниям с очень большой амплитудой а = 21,4 в, что практически можно считать неустойчивостью системы в большом. Поэтому уточнение решения с вычислением высших гармоник произведем только для первого периодического решения.

Для данной нелинейности (рис. 18.13, а) по формулам (18.191) находим выражения:

Из формул (18.192) и (18.68) получаем относительную амплитуду δ3 и фазу ϕ3 третьей гармоники в виде

Вычисление по этим формулам дает

Для уточнения первой гармоники за счет только что вычисленной третьей гармоники находим согласно (18.190) добавки к коэффициентам гармонической линеаризации:

подставляя которые в (18.188) согласно (18.68) придем к уточненному характеристическому уравнению

(18.200)

где аналогично (18.66) имеем:

(18.201)

Подставив в уравнение (18.200) р=jw и мнимую части, получим два уравнения:

Эти уточненные уравнения отличаются от прежних уравнений первого-приближения несколькими добавочными членами, но способ решения их остается прежним. Из последнего уравнения находим

(18.202).

а из первого

(18.203)

Задаваясь разными значениями амплитуды a1 и вычисляя каждый раз по формулам (18.201) — (18.203) значения q(а1), w1 и k, получим графики а1(k) типа рис. 18.14, но уже для уточненного значения амплитуды a1 первой гармоники периодического решения. Для заданного значения k = 140 это уточнение дает а1= 2,39 в, w1 = 117,8 сек-1. Значения эти достаточно близки к величинам первого приближения, а подсчитанная выше амплитуда третьей гармоники достаточно мала.

Пример 2. Пусть в системе автоматического регулирования используется двухфазный индукционный двигатель, описываемый нелинейным уравнением (18.119). В примере 7 § 18.3 найдены автоколебания для первого приближения в общем виде. Рассмотрим следующий числовой пример:

с двумя вариантами нелинейности; а) слабая нелинейность

б) сильная нелинейность

Расчет по формулам первого приближения (18.126) и (18.128) дает автоколебания в виде x=a sinwt, где для варианта слабой нелинейности

а для варианта сильной нелинейности

Вычислим теперь высшие гармоники. Для учета второй и третьей гармоник воспользуемся формулой (18.178). Для рассматриваемой в настоящем примере нелинейности F(х, рх) коэффициенты r2 и s2, подсчитанные по формулам (18.177), оказываются нулями. Поэтому остается только третья гармоника, для которой по формулам (18.177) для данной нелинейности с учетом обозначений (18.121) находим:

(18.204)

Тогда по формулам (18.179) с учетом того, что согласно (18.124)

находим относительную амплитуду и фазу третьей гармоники:

При указанных выше данных получаем для варианта слабой нелинейности

а для сильной нелинейности

После этого уточняется первая гармоника автоколебаний a1 sinw1t. Для этого по формулам (18.183) находим величины добавок ∆q и ∆q ' к коэффициентам гармонической

линеаризации:

Поэтому новое характеристическое уравнение для определения уточненной первой гармоники будет

Подставляя p=jw1 и выделяя вещественную и мнимую части, получим

Эти уравнения решаются тем же методом, что и (18.125), а именно: из второго уравнения получаем

а из первого

Эти уравнения приводят также к графику а1 (k) вида рис. 18.23, в. Для приведенных выше числовых значений параметров системы получаем следующие уточненные значения амплитуды и частоты автоколебаний:

для слабой нелинейности

для сильной нелинейности

Как видим, сильная нелинейность значительно снижает амплитуду автоколебаний (в линейной системе было бы а1 = ∞). Этот результат получался выше в решении по первому приближению и подтверждается теперь уточненным решением.

§ 18.6. Частотный метод определения автоколебаний

Здесь, следуя Л. С. Гольдфарбу [32, 121], будем рассматривать простые нелинейности х2=F(х1), так как в других случаях получаются более сложные графические построения. Пусть в нелинейной системе автоматического регулирования выделено, как обычно, нелинейное звено (рис. 16.1). Разомкнем систему указанным на рис. 18.38, а образом, причем уравнение нелинейного звена будет

(18.205)

а линейной части системы —

(18.206)

Замыкание системы соответствует замене

(18.207)

Подадим на вход нелинейного звена (рис. 18.38, а) синусоидальные колебания

(18.208)

На выходе нелинейного звена получим согласно (18.205) вынужденные колебания

(18.209)

которые можно найти, например, как показано на рис. 18.38, б или в. Разложим (18.209) в ряд Фурье и сохраним только основную синусоиду (первую

гармонику), отбросив все высшие гармоники. Очевидно, что это приближенное представление вынужденных колебаний эквивалентно гармонической линеаризации нелинейностей, рассмотренной в § 18.1.

На основании этого для определения первой гармоники вынужденных колебаний величины х2 можно воспользоваться частотным аппаратом, который применялся ранее для линейных систем, следующим образом.

Согласно формулам (18.9) приближенная передаточная функция нелинейного звена с уравнением х2 = F(х1) будет

и

соответственно при наличии гистерезисной петли и при отсутствии ее. При этом выражения q(а) и q'(а) определяются формулами (18.10).

Приближенный комплексный коэффициент усиления, или приближенная амплитуднофазовая характеристика нелинейного звена с уравнением x2 =F(x1)> при наличии гистерезисной петли, следовательно, будет

(18.210)

а без гистерезисной петли —

(18.211)

Эта приближенная амплитудно-фазовая характеристика определяет амплитуду и фазу первой гармоники на выходе нелинейного звена (если на его вход подается синусоида), а именно выражение (18.210) можно представить в виде

где

(18.212)

Следовательно, амплитуда первой гармоники на выходе будет а2 = аАн(а), а фазовый сдвиг — βн (а), где а — амплитуда на входе нелинейного звена. В результате получим

следующие вынужденные колебания на выходе нелинейного звена (первая гармоника):

Например, выходная величина x2 релейного звена с характеристикой рис. 18.1, а меняется в процессе вынужденных колебаний по закону, изображенному сплошной ломаной линией на рис. 18.38, в. Пунктиром показана основная синусоида для нее, причем из

(18.212) и (18.15) имеем:

Действительная ступенчатая кривая заменяется в данном случае синусоидой (первая гармоника), вершина которой совпадает с осью симметрии действительного прямоугольника (рис. 18.38, в).

Для нелинейных звеньев с уравнением вида x2 = F(х) без гистерезисной петли, как следует из § 18.1, q' (а) = 0. Следовательно, для таких звеньев Ан = q(а) и β1 = 0, т. е. вынужденные

колебания на выходе не имеют фазового сдвига.

Одним из главных отличий вынужденных колебаний нелинейных систем от линейных является их существенная зависимость не только от частоты, но и от амплитуды входных колебаний. Эту главную особенность как раз и улавливает написанное здесь приближенное выражение амплитудно-фазовой характеристики нелинейного звена. В формулах (18.210) — (18.212) получилась зависимость только от амплитуды а, потому что ограничились рассмотрением только нелинейности вида х2 = F(х1). Для более сложных нелинейных звеньев в амплитудно-фазовую характеристику войдет также и частота w. Кроме того, как увидим ниже, зависимость от частоты будет всегда вводиться линейной частью системы.

В § 18.1 были приведены выражения q(а) и q'(а) для наиболее типичных релейных и других простейших нелинейных звеньев. На основании этого строятся приближенные амплитудные и фазовые характеристики путем вычислений по формулам (18.212).

Результаты для простейших случаев приведены на рис. 18.39 и 18.40. Там приведены также и обратные амплитудно-фазовые характеристики

(18.213)

На графиках указаны все необходимые обозначения и типы нелинейных характеристик звеньев. Аналогичным путем можно построить графики и для других конкретных нелинейных звеньев.