Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975

(18.123)

где ϕ — отклонение регулируемой величины. Характеристическое уравнение всей замкнутой системы будет

(18.124)

где

После подстановки р =jw получаем:

(18.125)

Рассмотрим при этом влияние параметра k (общего коэффициента усиления регулятора). Второе из уравнений (18.125) дает

(18.126)

Из (18.121) видно, что b2 >b1. Поэтому полученная формула дает зависимость амплитуды ап от частоты wп искомого периодического решения в виде графика, показанного на рис. 18.23, б, где

(18.127)

Далее, первое из выражений (18.125) при w = wп и а =ап с использованием второго приводит к формуле для параметра k, влияние которого рассматривается:

(18.128)

По этой формуле, используя предыдущие результаты, получаем график зависимости амплитуды автоколебаний ап от величины параметра k, показанный на рис. 18.23, в. ,

§ 18.4. Нелинейные системы второго класса

Нелинейные системы второго класса — это системы с несколькими нелинейными звеньями или же с одним нелинейным звеном, когда под знаки нелинейных функций входят две или более переменных, связанных между собой линейными передаточными функциями или нелинейными уравнениями. Обычный прием приближенного решения, излагаемый ниже в примерах 1—3, справедлив при соблюдении условия фильтра, оговоренного в §18.2, для всех передаточных функций, связывающих указанные переменные. Если это условие не соблюдается, применяется специальный прием решения, изложенный ниже в примере 4.

Пример 1. В предыдущем параграфе рассматривалось влияние нелинейности привода, а затем влияние квадратичного трения по отдельности. Рассмотрим теперь совместное действие нелинейности привода и квадратичного трения. Момент трения при этом описывается нелинейным членом F(х), как в уравнении (18.90), или, что то же самое, графиком на рис. 18.24, а. Нелинейный привод пусть имеет характеристику типа насыщения (рис. 18.24,6).

Тогда уравнение двигателя и управляемого объекта вместо (18.90) примет вид

(18.129)

где F1 (iЯ)=Мвр и определяется графиком рис. 18.24, б.

В данном случае получается нелинейная система второго класса. Приближенно полагаем, что при автоколебаниях

(18.130)

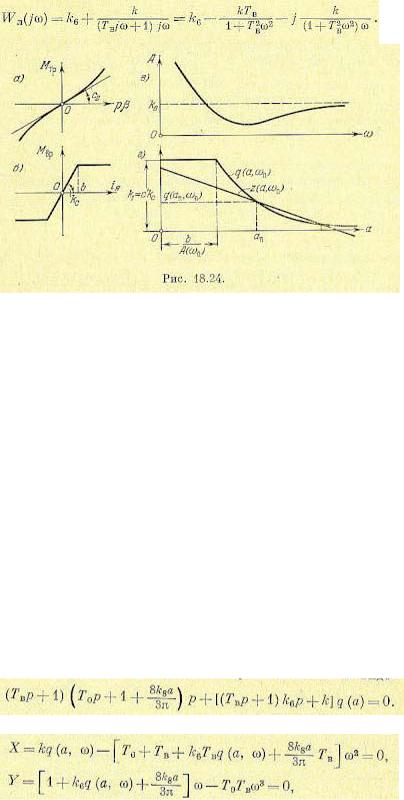
Из первого уравнения легко определяются все возможные значения амплитуды aп и частоты wп следующим образом.

Задаемся каким-нибудь значением wп. Из графика на рис. 18.24, в находим для него величину А(wп). По формуле (18.133) строим кривую q(а, ап), показанную на рис. 18.24, г. Обозначим далее правую часть первого из уравнений (18.134) через 2 (при переменной а вместо ап):

и проведем согласно этой формуле на том же рис. 18.24, г прямую z(а, wп). В точках пересечения получаем искомые значения амплитуды ап, а также и значения q(ап,wп). После этого по второй из формул (18.134) подсчитаем величину параметра b.

Проделав такую же операцию для различных значений wп и получая каждый раз ап и k, сможем построить и здесь графики, подобные тем, которые получались в предыдущих

Пример 2. Пусть в системе, функциональная блок-схема которой изображена на рис. 18.25, регулируемый объект описывается уравнением

(18.135)

измеритель 1 — нелинейный (рис. 18.26) —

(18.136)

измеритель 2 — линейный —

(18.137)

Составим теперь характеристическое уравнение всей замкнутой системы в гармонически линеаризованном виде. Согласно (18.135) — (18.140) получаем

(18,138)

Пренебрегая произведениями постоянных времени при высших степенях р по сравнению с их суммой, что вполне допустимо при рассмотрении низкочастотных автоколебаний

(которые здесь и будут, иметь место), запишем характеристическое уравнение в виде

Подстановка р =jw дает:

Подставив значение k0q2q1 из первого уравнения во второе, поделенное на w, получим (пренебрегая снова произведением T1T2w2 по сравнению с единицей)

(18-145)

Подставив это в первое уравнение (Х = 0) и пренебрегая опять-таки произведением Т1(Т1+Т3)w2 по сравнению с единицей, найдем

(18.146)

Последнее уравнение легко решается графически. Изобразим график <71 (а) согласно формуле (18.141). На рис. 18.28, а это показано сплошной .кривой. Пунктирная кривая показывает продолжение его при а >b2. Путь графического решения уравнения (18.146) показан сплошными стрелками. Этим определяется искомая амплитуда автоколебаний ап регулируемой величины х. Пунктирные стрелки дают второе решение ап2 (неустойчивое). Для определения частоты автоколебаний воспользуемся уравнением (18.145). Для этого сначала из формулы (18.144) найдем зависимость а3(w) при заданном значении (18.146), что ;после пренебрежения прежними малыми членами дает

(18.147)

где значение ап берется из графика рис. 18.28, а.

Имея выражение для q2 (а3) [одно из (18.142)], подставим в него полученное а3 (w). Это позволяет построить график q (w) (сплошная кривая на рис. 18.28, б). На тот же график наносим правую часть уравнения (18.145) (пунктирная кривая на рис. 18.28, б). Точка пересечения этих двух кривых дает искомое значение частоты автоколебаний wп как решение уравнения (18.145). После этого становится известной и амплитуда автоколебаний а3п на входе усилителя-преобразователя, вычисляемая по формуле (18.147) при найденном значении w = wп.

Пример 3. Рассмотрим систему, в которой нелинейным звеном является логическое устройство (рис. 16.25) с простейшим законом формирования сигнала управления (рис. 16.26). Уравнения системы заданы в виде (16.66) - (16.69).

1 Установившийся режим в такой системе будет автоколебательным. Искать его будем приближенно в синусоидальной форме

(18.148)

так как свойство фильтра в данной системе соблюдается. Тогда величины u и v будут

где

(18.149)

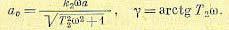(18.150)

В результате процесс изменения u и v в установившемся режиме будет иметь приблизительно вид некоторого эллипса (рис. 18.29, пунктир). Поэтому включение сигнала Ф в логическом устройстве при данной логике будет происходить от величины и (при u = ±u1, т. е. в точках А и С)г а выключение — от величины v (при v = ±v1, т. е. в точках D и В; рис. 18.29). Этот процесс во времени (ψ = wt ) изображен на рис. 18.30.

Точки включения и выключения определяются на оси абсцисс величинами ψ 1 и ψ 2 причем

Отсюда

(аналогично ψ 2 выражается через γ ). Учитывая, что согласно (18.149)

(аналогично γ выражается через T2w), находим

(18.151)

(18.152)

Теперь по правилам § 18.1 легко записать результат гармонической линеаризации нелинейной логической функции:

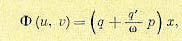(18.153)

где

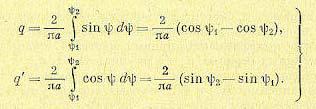(18.154)

Найденные значения q и q' согласно (18.151) и (18.152) являются вполне определенными функциями искомых величин а и w (амплитуды и частоты автоколебаний переменной х). Характеристическое уравнение рассматриваемой системы в целом после указанной гармонической линеаризации нелинейности, согласно (16.66) — (16.69) и (18.153), принимает вид

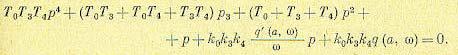(18.155)

Для отыскания синусоидального периодического решения подставляем р = jw. Получаем вещественную и мнимую части соответственно

Отсюда

(18.156)

(18.157)

Эти два уравнения с двумя неизвестными а и w решаются графически. Для этого по формулам (18.154) с учетом (18.151) и (18.152) строятся графики q(w) и q' (w) при разных значениях а = а1, а2, а3, . . . (рис. 18.31, а). Затем на первом из них наносится кривая 7, определяемая правой частью уравнения (18.156), а на втором — кривая (18.157). Решение определится точками пересечения, для которых значения а = ап и w = wп одинаковы на обоих графиках. Найденные значения ап и wп будут искомыми амплитудой и частотой автоколебаний, определяемых приближенно в виде х = ап sinwпt. Полученные конкретные числовые значения а = ап и w = wп соответствуют всем заданным )параметрам объекта и системы управления.

Если изменить параметры системы, изменятся также ап и wп. На том же графике можно проследить влияние изменения параметров системы, для чего 'нужно менять коэффициенты правых частей (18.156) и (18.157) при построении пунктирных кривых 1,1’

на рис. 18.31, а.

Изложенное выше решение удобно, если все параметры системы заданы. Для изучения же зависимости а и w от параметров системы (т. е. для выбора параметров) целесообразнее применить другой путь решения задачи. Допустим, необходимо выбрать общий коэффициент усиления с учетом влияния различных возможных значений постоянной T4. Тогда, исключая kоT3T4 из уравнений (18.156) и (18.157), находим

а затем

Задаваясь теперь различными значениями а и w и вычисляя каждый раз но этим формулам T4 и k0k3k4, получим сетку линий равных значений w (w1, w2, . . .) и а (а,1, а2, . . .),

показанных на рис. 18.31, б. По этой .диаграмме удобно выбирать значения параметров k0k3k4 и Т4 для получения желаемых а и w.

Кроме того, важными параметрами являются k1, k2 и особенно u1 и v1 (см. рис. 18.29). Но они входят в выражения q и q'. Поэтому для определения их влияния нужно построить графики q и q' для разных значений указанных параметров, а затем, задаваясь значениями а и w и используя соотношения (18.156) и (18.157), по «потребным» значениям q и q' определять эти параметры (u1, v1, k1 или k2). При этом нужно учитывать, что из требования вещественности выражений (18.151) и (18.152) следует выбирать

Пример 4. Рассмотрим систему автоматического регулирования с двумя нелинейностями в случае, когда их гармоническая линеаризация по отдельности невозможна вследствие отсутствия свойства фильтра у звена, стоящего между ними (рис.

.18.32).

Представим весь блок, включающий обе нелинейности, изображенный отдельно на рис. 18.33, как одно нелинейное звено. По отношению к нему система обладает свойством фильтра. Следовательно, автоколебания в системе можно искать приближенно в виде

Система уравнений, описывающих работу всей системы, имеет вид

(18.158)

Чтобы найти передаточную функцию нового нелинейного блока (рис. 18.33), определим его выходной сигнал x2 (t) при входном сигнале х1 = а sinwt. Это представлено на рис.

18.34. Отсюда видно, что выходной сигнал х2 представляет собой ограниченные на уровне b треугольные колебания, отстающие по фазе от входного сигнала на угол

ϕ ≤π / 2 . Если время перехода выходного сигнала из одного крайнего положения в другое составляет tп, угол ϕ определяется соотношением

С учетом того, что tп=2b/c, T= 2πw , получаем

(18.159)

Для того чтобы выходной сигнал достигал уровня ограничения (т. е. чтобы вторая нелинейность участвовала в работе), необходимо выполнение условия

Таким образом, следует рассматривать входные сигналы с частотой

(18.160)

Амплитуда первой гармоники для треугольного сигнала с ограничением имеет вид

(18.161)

Следовательно, первая гармоника сигнала х2 будет

(18.162)

В результате можно записать уравнение нелинейного блока (рис. 18.33) в гармонически линеаризованном виде:

(18.163)

где

(18.164)

Характеристическое уравнение всей замкнутой системы при этом получит вид

(18.165)

Для удобства дальнейших преобразований представим q и q’/w в виде

(18.166)

где Q1 и Q2 зависят от частоты w, а от амплитуды а не зависят. Будем искать частоту wп и амплитуду ап автоколебаний путем подстановки р = jw в (18.165), что дает:

(18,167)

(18.168)

Поскольку a ≠ 0 можно найти частоту wп:

(18.169)

Так как в Q1 и Q2 входит wп под знаком тригонометрических функций, решаем это уравнение графически. Его левая часть изображается кривой, показанной на рис. 18.35.

В результате получаются два значения частоты периодического решения: wп = w1 и

wп = w2.

Преобразуем уравнение (18.168) к виду

(18.170)

Отсюда, подставляя значения полученных при решении уравнения (18.169) частот, можно найти амплитуду периодического решения ап сигнала на входе нелинейного звена. Остается определить, которое из двух найденных решений соответствует действительным автоколебаниям в системе. Для этого исследуем устойчивость найденного решения с помощью критерия (18.63).

Поскольку согласно (18.167)

частная производная

так как выражение F1(w) представляет собой (18.169), обращающуюся в нуль при w= wп

Для отыскания ∂∂Ya представим Y в виде

Тогда

так как выражение F2 (а, w) представляет собой левую часть уравнения (18.170), образующуюся в нуль при w = wп, а = ап, а частная производная

В результате условие устойчивости автоколебаний (18.63) сводится к требованию

(18.171)

При отыскании частоты wп автоколебаний по уравнению (18.169) был построен график. Из рассмотрения этой кривой (рис. 18. 35) видно, что условие устойчивости (18.171) выполняется для большего из найденных значений частоты wп =w2. Таким образом, в системе существуют автоколебания, параметры которых определяются указанными значениями частоты wп = w2.

Помимо условия (18.171) для устойчивости найденного решения необходимо, чтобы все коэффициенты характеристического уравнения (18.165) были положительными, а именно:

Легко проверить, что все эти условия были выполнены в самом процессе отыскания периодического решения.

§ 18.5. Вычисление высших гармоник и уточнение первой гармоники автоколебаний

Пусть задано дифференциальное уравнение нелинейной системы

(18.172)

До сих пор периодическое решение (автоколебания) для нелинейной системы искалось для первого приближения в виде

(18.173)

что соответствовало приближенному значению первой гармоники периодического решения. Все высшие гармоники при этом отбрасывались ввиду их малости при наличии в системе свойства фильтра(§ 18.2).

Оставляя в силе это условие, произведем отыскание малых высших гармоник [100], введя отдельное обозначение для каждой k-й гармоники:

(18.174)

где амплитуда k-й гармоники δk a выражена через амплитуду первой гармоники а, причем коэффициент δk является малой величиной (так как амплитуда высшей гармоники предполагается малой по сравнению с амплитудой первой гармоники). Величину δk ,

играющую в данной задаче роль малого параметра, можно назвать относительной амплитудой k-й гармоники.

Теперь с учетом конечного числа n высших гармоник искомое периодическое решение (автоколебания) запишется в виде

(18.175)

где

обозначает уточненную по сравнению с (18.173) первую гармонику автоколебаний. Поскольку амплитуды высших гармоник δk a малы, то их вычисление можно

производить, используя первое приближение периодического решения (18.173), так как использование уточненного решения (18.175) внесло бы в определение бди несущественные малые высшего порядка, но зато привело бы к неразрешимой системе уравнений.

Это чрезвычайно важное (для вычисления высших гармоник автоколебаний) допущение можно иначе сформулировать следующим образом. Считая, что на входе х нелинейного звена (рис. 18.36) истинное периодическое решение (18.175) (при n → ∞) мало отличается