
Определение первообразной и неопределенного интеграла. Основные свойства.
Первообразной данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.
Свойства:
Если F(х) одна из первообразных для функции f(х) на промежутке J, то множество всех первообразных этой функции имеет вид: F(х)+С, где С - любое действительное число.
Множество первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается символом
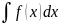 .
.
Основные свойства
1.
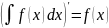
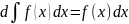
2.
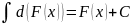
3.
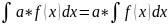
4.
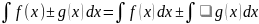
Если
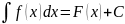 ,
то и
,
то и
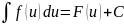 ,
где
,
где
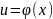 -- произвольная функция, имеющая
непрерывную производную.
-- произвольная функция, имеющая
непрерывную производную.
Интегрирование путём замены переменной. Подстановка и подведение под знак дифференциала.
Метод интегрирования путём замены переменной заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Эквивалентен сказанному выше.
Интегрирование по частям в неопределенном интеграле.
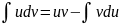
Рассмотрим
пример
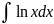 :
:
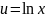 ;
;
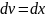
То есть, за
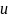 мы обозначили логарифм, а за
мы обозначили логарифм, а за
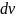 – оставшуюся часть подынтегрального
выражения.
– оставшуюся часть подынтегрального
выражения.
Находим дифференциал
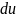
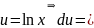 ;
;
Теперь открываем наше решение и конструируем правую часть формулы:
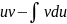
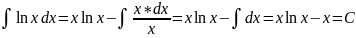 ,
где
,
где

Таблица интегралов
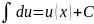
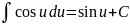
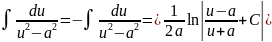
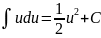
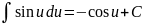
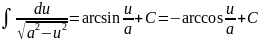
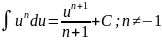
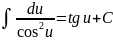
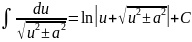
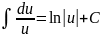
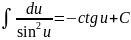
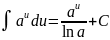
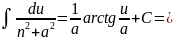
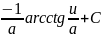 (высокий)
(высокий)Определение интегральной суммы Римана и определенного интеграла (5 пунктов), его геометрический смысл. Формула Ньютона - Лейбница.
Если существует предел интегральной суммы при стремлении к нулю длины наибольшего частичного интервала разбиения:
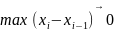 ,
,
то
функция
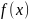 называется интегрируемой
в смысле Римана
на интервале
называется интегрируемой
в смысле Римана
на интервале
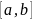 .
Предел этой суммы
.
Предел этой суммы
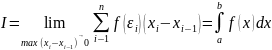 ,
,
называется
определенным
интегралом
от
по
интервалу
в смысле Римана
(интеграл
Римана).
Это определение означает, что для любого
положительного числа
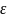 существует такое число
существует такое число
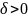 ,
что при любом разбиении интервала
на частичные интервалы, длины которых
меньше
,
что при любом разбиении интервала
на частичные интервалы, длины которых
меньше
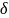 .
.
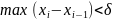
и
при любом выборе промежуточных точек
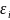 выполняется неравенство
выполняется неравенство
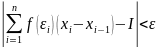 .
.
Функция
f(x)
называется подынтегральной
функцией,
а
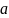 и
и
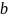 - пределами
интегрирования.
- пределами
интегрирования.
Формула Ньютона-Лейбница (формула двойной подстановки)
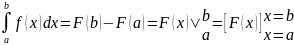
(f непрерывна; F - первообразная для f).
Несобственные интегралы 1 и 2 рода.
Если существует предел интегральной суммы при стремлении к нулю длины наибольшего частичного интервала разбиения:
,
то функция называется интегрируемой в смысле Римана на интервале . Предел этой суммы
,
называется определенным интегралом от по интервалу в смысле Римана (интеграл Римана). Это определение означает, что для любого положительного числа существует такое число , что при любом разбиении интервала на частичные интервалы, длины которых меньше .
и при любом выборе промежуточных точек выполняется неравенство
.
Функция f(x) называется подынтегральной функцией, а и - пределами интегрирования.
Формула Ньютона-Лейбница (формула двойной подстановки)
(f непрерывна; F - первообразная для f).
Несобственные интегралы 1 и 2 рода. Определения, признаки сравнения, интегралы сравнения.
Несобственный интеграл - определенный интеграл от непрерывной функции, но с бесконечным промежутком интегрирования или определенный интеграл с конечным промежутком интегрирования, но от функции, имеющей на нем бесконечный разрыв.
Интеграл с бесконечным промежутком интегрирования (несобственный интеграл I рода)
Пусть
функция
непрерывна на промежутке
 .
Если существует конечный предел
.
Если существует конечный предел
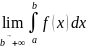 ,
то его называют несобственным
интегралом первого рода и
обозначают
,
то его называют несобственным
интегралом первого рода и
обозначают
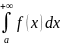 .
.
Таким
образом, по определению
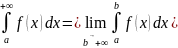 .
.
В этом случае говорят, что несобственный интеграл сходится.
Если же указанный предел не существует или он бесконечен,то говорят, что интеграл расходится.
Аналогичноопределяется несобственный интеграл на промежутке :
 ,
,
Несобственный интеграл с двумя бесконечны ми пределами определяется формулой
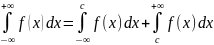 ,
,
где с — произвольное число.
В
этом случае интеграл слева сходится
лишь тогда, когда сходятся оба интеграла
справа. Отметим, что если непрерывная
функция
 на промежутке
и интеграл
на промежутке
и интеграл
 сходится,
то он выражает площадь бесконечно
длинной криволинейной трапеции.
сходится,
то он выражает площадь бесконечно
длинной криволинейной трапеции.
Интеграл от разрывной функции (несобственный интеграл II рода)
Пусть
функция
непрерывна на промежутке
и имеет бесконечный разрыв при
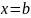 .
Если существует конечный предел
.
Если существует конечный предел
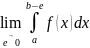 , то
его называют несобственным интегралом
второго рода и обозначают
, то
его называют несобственным интегралом
второго рода и обозначают
 .
.
Таким образом, по определению,
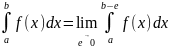 .
.
Если предел в правой части существует, то несобственный интеграл сходится. Если же указанный предел не существует или бесконечен, то говорят, что интеграл расходится.
Аналогично,
если функция
терпит бесконечный разрыв в точке
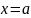 ,
то полагают
,
то полагают
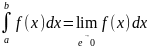 .
.
Если
функция
терпит разрыв во внутренней точке с
отрезка
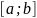 ,
то несобственный интеграл второго рода
определяется формулой
,
то несобственный интеграл второго рода
определяется формулой
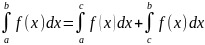 .
.
В
этом случае интеграл слева называют
сходящимся, если оба несобственных
интеграла, стоящих справа, сходятся. В
случае, когда
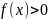 ,
несобственный интеграл второго рода
(разрыв
в точке
)
можно истолковать геометрически как
площадь бесконечно высокой криволинейной
трапеции.
,
несобственный интеграл второго рода
(разрыв
в точке
)
можно истолковать геометрически как
площадь бесконечно высокой криволинейной
трапеции.
Двойной интеграл: определение (5пунктов), геометрический смысл. Повторный интеграл.
Двойной интеграл - это обобщение определенного интеграла на двумерный случай. Т.е. для определения понятия двойного интеграла используется функция, зависящая уже от двух переменных: f(x,y). Эта функция должна быть определена на некоторой, обладающей конечной площадью, области D плоскости X0Y. При этом граница области D должна состоять из конечного числа графиков непрерывных функций.
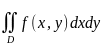
Геометрический смысл двойного
интеграла: при неотрицательной функции
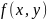 ,
двойной интеграл по области
,
двойной интеграл по области
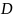 представляет из себя объем криволинейного
цилиндра, который построен на области
и ограничен сверху поверхностью
представляет из себя объем криволинейного
цилиндра, который построен на области
и ограничен сверху поверхностью
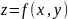 .
.
Вычисление двойного интеграла
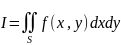 от функции
по области
от функции
по области
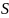 ,
ограниченной прямыми
,
ограниченной прямыми
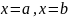 и кривыми
и кривыми
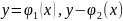 ,
при некоторых условиях относительно
функций
,
при некоторых условиях относительно
функций
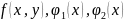 ,
производится по формуле:
,
производится по формуле:
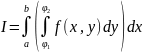
где при вычислении внутреннего интеграла
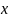 считается постоянным. Таким образом,
вычисление двойного интеграла сводится
к двум вычислениям обычных интегралов,
или, как говорят, к повторному интегралу.
Геометрически сведение двойного
интеграла к повторному интегралу
означает возможность вычисления объёма
цилиндроида как путём разбиения его на
элементарные столбики, так и путём
разбиения его на элементарные слои,
параллельные плоскости
считается постоянным. Таким образом,
вычисление двойного интеграла сводится
к двум вычислениям обычных интегралов,
или, как говорят, к повторному интегралу.
Геометрически сведение двойного
интеграла к повторному интегралу
означает возможность вычисления объёма
цилиндроида как путём разбиения его на
элементарные столбики, так и путём
разбиения его на элементарные слои,
параллельные плоскости
 .
При некоторых условиях на функцию
область
в повторных интегралах можно изменить
порядок интегрирования (то есть сначала
интегрировать по
,
а потом по
.
При некоторых условиях на функцию
область
в повторных интегралах можно изменить
порядок интегрирования (то есть сначала
интегрировать по
,
а потом по
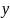 ).
Аналогично определяется повторный
интеграл в случае функций большего
числа переменных.
).
Аналогично определяется повторный
интеграл в случае функций большего
числа переменных.
Полярная система координат. Элемент площади в полярной системе. Якобиан.
Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом.
Полярная
система координат задаётся лучом,
который называют нулевым или полярной
осью. Точка, из которой выходит этот луч
называется началом координат или
полюсом. Любая точка на плоскости
определяется двумя полярными координатами:
радиальной и угловой. Радиальная
координата (обычно обозначается
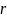 )
соответствует расстоянию от точки до
начала координат. Угловая координата,
также называется полярным углом или
азимутом и обозначается
)
соответствует расстоянию от точки до
начала координат. Угловая координата,
также называется полярным углом или
азимутом и обозначается
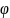 ,
равна углу, на который нужно повернуть
против часовой стрелки полярную ось
для того, чтобы попасть в эту точку.
,
равна углу, на который нужно повернуть
против часовой стрелки полярную ось
для того, чтобы попасть в эту точку.
Определённая таким образом радиальная координата может принимать значения от нуля до бесконечности, а угловая координата изменяется в пределах от 0° до 360°. Однако, для удобства область значений полярной координаты можно расширить за пределы полного угла, а также разрешить ей принимать отрицательные значения, что отвечает повороту полярной оси по часовой стрелке.
Пусть
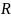 —
область, которую образуют полярная
кривая
—
область, которую образуют полярная
кривая
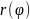 и лучи
и лучи
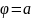 и
и
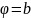 ,
где
,
где
 .
Тогда площадь этой области находится
определённым интегралом:
.
Тогда площадь этой области находится
определённым интегралом:

Определитель матрицы Якоби
Также якобианом иногда называют саму матрицу Якоби, а не её определитель.
По-английски и в некоторых других языках термин якобиан считается равно приложимым к матрице Якоби и её определителю.
Матрица
Я́ко́би
отображения
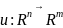 в точке
в точке
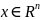 описывает главную линейную часть
произвольного отображения
в точке
.
описывает главную линейную часть
произвольного отображения
в точке
.
Тройной интеграл: определение, геометрический смысл.
Схоже с двойным, только считает как множество кубиков внутри объемного тела (кубированием).
Понятия: дифференциальное уравнение; порядок дифференциального уравнения; общее, частное и особое решения; их геометрический смысл. Задача Коши.
Дифференциальное уравнение — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, её производные и независимые переменные; однако не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением. Например,
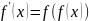 не является дифференциальным уравнением.
не является дифференциальным уравнением.Порядком дифференциального уравнения называется максимальный порядок производной от искомой функции, входящей в данное уравнение.
Рассмотрим примеры:
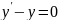 – дифференциальное
уравнение 1 – го порядка;
– дифференциальное
уравнение 1 – го порядка;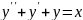 – дифференциальное
уравнение 2 – го порядка;
– дифференциальное
уравнение 2 – го порядка;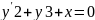 –
дифференциальное
уравнение 1 – го порядка;
–
дифференциальное
уравнение 1 – го порядка;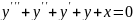 – дифференциальное
уравнение 3 – го порядка;
– дифференциальное
уравнение 3 – го порядка;
Во
всех этих дифференциальное уравнение
 – неизвестная функция.
– неизвестная функция.
Общее решение дифференциального уравнения — функция наиболее общего вида, которая при подстановке в дифференциальное уравнение вида
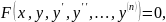
обращает его в тождество.
Частным решением дифференциального уравнения на интервале
 называется каждая функция
называется каждая функция
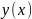 ,
которая при подстановке в уравнение
вида
,
которая при подстановке в уравнение
вида
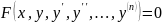 обращает
его в верное тождество на интервале
.
обращает
его в верное тождество на интервале
.
Зная общее решение однородного дифференциального уравнения и любое частное решение неоднородного уравнения, можно получить общее решение неоднородного уравнения в виде суммы общего решения однородного уравнения и частного решения неоднородного.
Особое решение обыкновенного дифференциального уравнения — решение, в любой окрестности каждой точки которого нарушается единственность решения задачи Коши для этого уравнения.
Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).
Задача Коши обычно возникает при анализе процессов, определяемых дифференциальным законом эволюции и начальным состоянием (математическим выражением которых и являются уравнение и начальное условие). Этим мотивируется терминология и выбор обозначений: начальные данные задаются при t = 0, а решение отыскивается при t > 0.
От краевых задач задача Коши отличается тем, что область, в которой должно быть определено искомое решение, здесь заранее не указывается. Тем не менее, задачу Коши можно рассматривать как одну из краевых задач.
Основные вопросы, которые связаны с задачей Коши, таковы:
Существует ли (хотя бы локально) решение задачи Коши?
Если решение существует, то какова область его существования?
Является ли решение единственным?
Если решение единственно, то будет ли оно корректным, то есть непрерывным (в каком-либо смысле) относительно начальных данных?
Говорят,
что задача Коши имеет единственное
решение, если она имеет решение
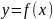 и никакое другое решение не отвечает
интегральной кривой, которая в сколь
угодно малой выколотой окрестности
точки
и никакое другое решение не отвечает
интегральной кривой, которая в сколь
угодно малой выколотой окрестности
точки
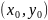 имеет поле направлений, совпадающее с
полем направлений
.
Точка
задаёт начальные условия.
имеет поле направлений, совпадающее с
полем направлений
.
Точка
задаёт начальные условия.
Дифференциальные уравнения 1 порядка с разделяющимися переменными и линейные.
Дифференциальное уравнение вида
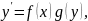 или
или
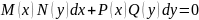
называется дифференциальным уравнением с разделяющимися переменными.
Заметим, что в данных дифференциальных уравнениях каждая из функций зависит только от одной переменной, т.е. происходит разделение переменных.
Для решения такого дифференциального
уравнения необходимо домножить или
разделить обе части дифференциального
уравнения на такое выражение, чтобы
в одну часть уравнения входили только
функции от
и
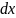 ,
в другую часть уравнения - только функции
от
,
,
в другую часть уравнения - только функции
от
,
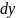 .
Затем в полученном дифференциальном
уравнении надо проинтегрировать обе
части:
.
Затем в полученном дифференциальном
уравнении надо проинтегрировать обе
части:
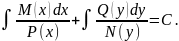
Следует заметить, что при делении обеих частей дифференциального уравнения на выражение, содержащее неизвестные и , могут быть потеряны решения, обращающие это выражение в ноль.
Обратим внимание, что дифференциальные уравнения с разделяющимися переменными легко сводятся к интегрированию. В общем случае получаем получаем два неопределенных интеграла.
Обыкновенное дифференциальное уравнение вида
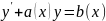
называется линейным дифференциальными уравнениями. Для его решения обычно используют метод вариации постоянной. Для этого сначала необходимо решить соответствующее однородное дифференциальное уравнение
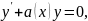
которое является дифференциальным
уравнением с разделяющимися переменными.
Полученное общее решение
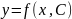 этого уравнения надо подставить в
исходное обыкновенное дифференциальное
уравнение, неоднородное дифференциальное
уравнение, считая, что
этого уравнения надо подставить в
исходное обыкновенное дифференциальное
уравнение, неоднородное дифференциальное
уравнение, считая, что
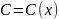 .
Затем необходимо решить полученное
обыкновенное дифференциальное
уравнение относительно неизвестной
функции
.
Затем необходимо решить полученное
обыкновенное дифференциальное
уравнение относительно неизвестной
функции
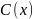 и подставить его решение в ранее
полученную формулу
.
и подставить его решение в ранее
полученную формулу
.
Фундаментальная система решений. Структура общего решения линейного однородного и неоднородного уравнения высшего порядка.
Любые n линейно независимых решений линейного однородного дифференциального уравнения n-ного порядка называется фундаментальной системой решений этого уравнения.
Найти фундаментальную систему решений
системы уравнений:
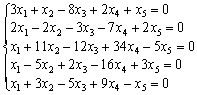 Решение
Найдем
ранг матрицы А:
Решение
Найдем
ранг матрицы А:
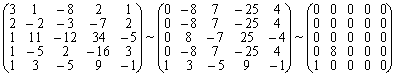 .
Итак, rang(A)=2. Оставляем в системе последние
два уравнения и переносим слагаемые со
свободными неизвестными в правую часть
системы:
.
Итак, rang(A)=2. Оставляем в системе последние
два уравнения и переносим слагаемые со
свободными неизвестными в правую часть
системы:
![]() Находим общее решение:
Находим общее решение:
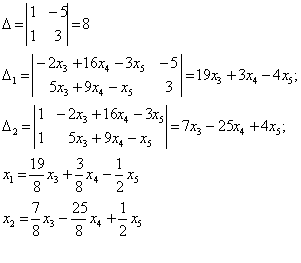 Чтобы найти
фундаментальную систему решений, нужно
выбрать произвольный отличный от нуля
определитель.
Представим его
в простейшем виде:
Чтобы найти
фундаментальную систему решений, нужно
выбрать произвольный отличный от нуля
определитель.
Представим его
в простейшем виде:
![]() .
Берем строки этого определителя
как значения свободных неизвестных,
получим 3 решения, которые образовывают
фундаментальную систему решений:
.
Берем строки этого определителя
как значения свободных неизвестных,
получим 3 решения, которые образовывают
фундаментальную систему решений:
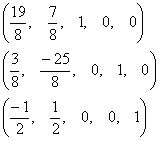
Признак линейной независимости частных решений ЛОДУ.
Построение фундаментальной системы решений ЛОДУ с постоянными коэффициентами.
Ряд. Частичная сумма ряда. Сумма ряда. Необходимое условие сходимости.
Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда).
Рассматриваются числовые ряды двух видов:
вещественные числовые ряды — изучаются в математическом анализе;
комплексные числовые ряды — изучаются в комплексном анализе;
Важнейший вопрос исследования числовых рядов — это сходимость числовых рядов.
Числовые ряды применяются в качестве системы приближений к числам.
Сумма
числового ряда
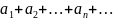 определяется как предел, к которому
стремятся суммы первых
определяется как предел, к которому
стремятся суммы первых
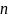 слагаемых ряда, когда
неограниченно растёт. Если такой предел
существует и конечен, то говорят, что
ряд сходится, в противном случае — что
он расходится. Элементы ряда
слагаемых ряда, когда
неограниченно растёт. Если такой предел
существует и конечен, то говорят, что
ряд сходится, в противном случае — что
он расходится. Элементы ряда
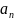 представляют собой либо вещественные,
либо комплексные числа.
представляют собой либо вещественные,
либо комплексные числа.
Пусть
— числовой ряд. Число
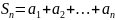 называется
называется
 -ой
частичной суммой
ряда
-ой
частичной суммой
ряда
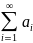 .
.
Сумма
(числового) ряда —
это предел частичных сумм
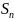 ,
если он существует и конечен. Таким
образом, если существует число
,
если он существует и конечен. Таким
образом, если существует число
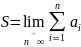 ,
то в этом случае пишут
,
то в этом случае пишут
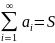 .
Такой ряд называется сходящимся.
Если предел частичных сумм не существует
или бесконечен, то говорят, что ряд
расходится.
.
Такой ряд называется сходящимся.
Если предел частичных сумм не существует
или бесконечен, то говорят, что ряд
расходится.
Ряд
может сходиться лишь в том случае, когда
член
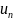 (общий член ряда) стремится к нулю:
(общий член ряда) стремится к нулю:
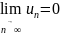 .
.
Это необходимый признак сходимости ряда (но не достаточный!). Если же общий член ряда не стремится к нулю — это достаточный признак расходимости.
Признаки сравнения числовых положительных рядов. Признак Даламбера.
Рассмотрим два положительных числовых ряда
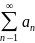 и
и
 .
Если
известно,
что ряд
–
сходится,
и выполнено неравенство
.
Если
известно,
что ряд
–
сходится,
и выполнено неравенство
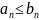 (для
(для
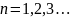 ),
то ряд
тоже
сходится.
),
то ряд
тоже
сходится.
Иными
словами: из
сходимости ряда с б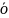 льшими
членами следует сходимость ряда с
меньшими членами.
льшими
членами следует сходимость ряда с
меньшими членами.
Предельный признак сравнения: Рассмотрим два положительных числовых ряда и . Если предел отношения общих членов этого ряда равен конечному, отличному от нуля числу
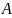 :
:
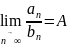 ,
то
оба ряда сходятся или расходятся
одновременно.
,
то
оба ряда сходятся или расходятся
одновременно.
Когда применяется предельный признак сравнения? Предельный признак сравнения применяется тогда, когда «начинкой» ряда у нас являются многочлены. Либо один многочлен в знаменателе, либо многочлены и в числителе и в знаменателе. Один или оба многочлена также могут находиться под корнем.
Признак Даламбера: Рассмотрим положительный числовой ряд . Если существует предел отношения последующего члена к предыдущему:
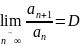 ,
то:
а) При
,
то:
а) При
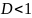 ряд
сходится.
В частности, ряд сходится при
ряд
сходится.
В частности, ряд сходится при
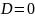 .
б)
При
.
б)
При
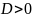 ряд
расходится.
В частности, ряд расходится при
ряд
расходится.
В частности, ряд расходится при
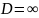 .
в)
При
.
в)
При
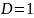 признак
не дает ответа.
Нужно использовать другой признак.
Чаще всего единица получается в том
случае, когда признак Даламбера пытаются
применить там, где нужно использовать
предельный признак сравнения.
признак
не дает ответа.
Нужно использовать другой признак.
Чаще всего единица получается в том
случае, когда признак Даламбера пытаются
применить там, где нужно использовать
предельный признак сравнения.
Эталонные ряды.
Знакопеременные ряды. Теорема Лейбница. Следствие.
