Числовой
ряд, содержащий бесконечное множество
положительных и бесконечное множество
отрицательных членов, называется
знакопеременным.
Частным случаем знакопеременного ряда
является знакочередующийся
ряд,
то есть такой ряд, в котором последовательные
члены имеют противоположные знаки.
Теорема (признак) Лейбница
Для знакочередующихся рядом действует
достаточный признак сходимости
Лейбница.
Пусть
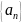 является числовой последовательностью,
такой, что
является числовой последовательностью,
такой, что
1.
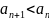 для всех
;
2.
для всех
;
2.
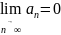 .
.
Тогда
знакочередующиеся ряд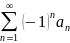 ы
и
ы
и
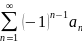 сходятся.
сходятся.
Из теоремы Лейбница вытекает следствие,
позволяющее оценить погрешность
вычисления неполной суммы ряда:
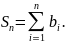
Остаток сходящегося знакочередующегося
ряда
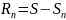 будет по модулю меньше первого отброшенного
слагаемого:
будет по модулю меньше первого отброшенного
слагаемого:
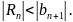
Функциональные ряды.
Область сходимости и расходимости.
Общий член рядов Тейлора и Маклорена.
Условие разложимости функции в ряд
Тейлора и Маклорена. Стандартные
разложения.
Функциональный ряд — ряд, каждым
членом которого, в отличие от числового
ряда, является не число, а функция
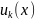 .
.
Область
сходимости (расходимости) – такое
множество значений
,
при котором ряд будет сходится
(расходится).
Тейлора:
Пусть
функция
бесконечно дифференцируема в некоторой
окрестности точки a.
Формальный ряд
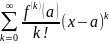
называется
рядом Тейлора функции f
в точке a.
Маклорена
– тоже самое, только при
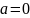 ,
тоесть
,
тоесть
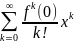
Пусть
функция
имеет на интервале
 ,
производные всех подяков и
,
производные всех подяков и
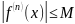 ,
для всех
,
для всех
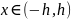 и для всех
и для всех
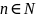 ,
тогда
разложима на интервале
,
тогда
разложима на интервале
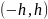 в степенной ряд вида
в степенной ряд вида
 .
.
Стандартные
разложения. Для однозначных функций
разложения в ряд Тейлора в принципе не
могут отличиться от изучавшихся в
прошлом семестре разложений:
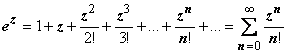 ;
;
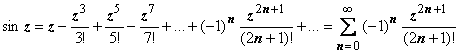 ;
;
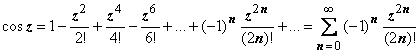 ;
;
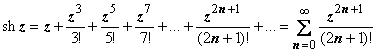 ;
;
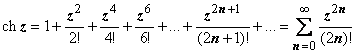 ;
;


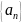 является числовой последовательностью,
такой, что
является числовой последовательностью,
такой, что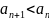 для всех
;
2.
для всех
;
2.
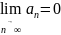 .
.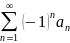 ы
и
ы
и
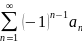 сходятся.
сходятся.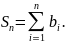
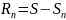 будет по модулю меньше первого отброшенного
слагаемого:
будет по модулю меньше первого отброшенного
слагаемого: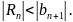
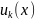 .
.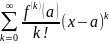
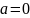 ,
тоесть
,
тоесть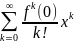
 ,
производные всех подяков и
,
производные всех подяков и
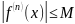 ,
для всех
,
для всех
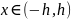 и для всех
и для всех
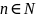 ,
тогда
разложима на интервале
,
тогда
разложима на интервале
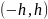 в степенной ряд вида
в степенной ряд вида
 .
.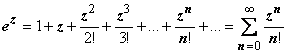 ;
;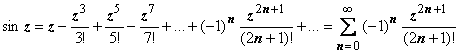 ;
;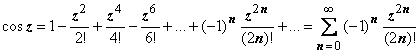 ;
;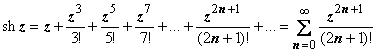 ;
;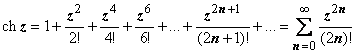 ;
;