Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975

Амплитудно-фазовая характеристика линейной части системы согласно (18.206) имеет вид

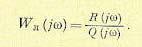(18.214)

Общая приближенная амплитудно-фазовая характеристика всей разомкнутой цепи с нелинейным звеном будет

(18.215)

Следовательно, амплитуда и фаза первой гармоники выходной величины х3, определяемые формулами

(18.216)

зависят здесь не только от частоты w, как в линейных системах, но еще и от величины входной амплитуды а.

Отыскание автоколебаний замкнутой системы. Незатухающие синусоидальные колебания с постоянной амплитудой в замкнутой системе определяются согласно частотному критерию устойчивости (см. § 6.5) прохождением амплитудно-фазовой характеристики разомкнутой системы через точку (—1, j0), т. е. равенством W = -1. Это и будет в данном случае условием существования периодического решения для замкнутой нелинейной системы, которое принимается приближенно синусоидальным. Итак, имеем условие

Учитывая (18.215) и (18.213), это можно записать в виде

(18.217)

или

(18.218)

где q' (а) = 0 в случае отсутствия гистерезисной петли (правая часть (18.218) в этом случае будет вещественной).

Левая часть уравнения (18.218) или (18.217) представляет собой амплитудно-фазовую характеристику линейной части системы, а правая — обратную амплитудно-фазовую характеристику нелинейного звена (для первой гармоники), взятую с обратным знаком.

Решение этого уравнения можно получить графически как точку пересечения указанных двух характеристик (рис. 18.41, а и б). В точке пересечения из кривой Wл (jw) берем значение частоты wп а из кривой — Мн (а) берем величину амплитуды ап искомого периодического решения. Рис. 18.41, а соответствует системе с нелинейным звеном, имеющим гистерезисную петлю, когда согласно (18.210) и (18.213) характеристика Мн(0) комплексна. При отсутствии гистерезисной петли, когда Мн (a) вещественна, получаем график рис. 18.41,б.

Вместо (18.217) можно пользоваться также выражением

(18.219)

т. е. искать решение как точку пересечения амплитудно-фазовой характеристики нелинейного звена с обратной амплитудно-фазовой характеристикой линейной части системы, взятой с обратным знаком (рис. 18.41, в ж г).

Устойчивость найденного периодического решения грубо оценивается следующим образом (этот метод не является строго обоснованным, но во многих случаях его применения достаточно). Дадим малое приращение амплитуде: а = aп + ∆a. Тогда при положительном ∆a получим на кривой — Мн (а), например, точку a1 (рис. 18.42, а), а при отрицательном ∆a — точку a2. Для устойчивости периодического решения требуется, очевидно, чтобы при положительном ∆a колебания затухали, а при отрицательном ∆a — расходились. Для этого согласно частотному критерию (§ 6.5) в случае устойчивой или нейтральной разомкнутой цепи требуется, чтобы суммарная амплитудно-фазовая характеристика W(a, w) в первом случае не охватывала точку (—1,j0), а во

втором — охватывала. Но общая характеристика W(a, w) не чертится в рассмотренном способе. Поэтому высказанное положение надо перенести на свойства кривых Wл(jw) и

—Мн (а).

Отсюда получаем, что для устойчивости периодического решения (если линейная часть системы в разомкнутом состоянии устойчива или нейтральна) требуется, чтобы амплитудно-фазовая характеристика линейной части W(jw) не охватывала точку a1 соответствующую положительному ∆a, и охватывала точку а2, соответствующую отрицательному ∆a. По этому признаку графики рис. 18.42, а и б (в точке В) дают устойчивое периодическое решение, которое соответствует автоколебаниям замкнутой системы с частотой wп2 и амплитудой ап2.

На графике рис,. 18.42, в значения wП1 и ап1 соответствуют неустойчивому, а значения wп2, ап2 — устойчивому периодическому решению. Это в простейшем случае может означать устойчивость системы в малом (до амплитуды яп1) и автоколебания с частотой wп2 и амплитудой ап2, если начальная амплитуда колебаний в переходном процессе превышает

значения ап1.

В таких исследованиях предполагается, что все параметры системы заданы в числовом виде (или амплитудно-фазовые характеристики звеньев в виде определенных графиков). Если же требуется выяснить влияние одного или двух каких-нибудь параметров системы, то надо рассмотреть все возможные комбинации кривых Wл (jw) и — Мн (а) при разных значениях этих параметров.

Рассмотрим примеры.

Система автоматического регулирования температуры. Уравнения системы автоматического регулирования температуры с релейным звеном были описаны в примере

5 § 18.3. Выражение амплитудно-фазовой характеристики линейной части системы с добавлением жесткой обратной связи будет

(18.220)

В данном случае очевидно, что общий знаменатель передаточной функции линейной части системы

(18.221)

не имеет корней с положительной вещественной частью, а нулевой корень говорит о том, что линейная часть системы нейтральна.

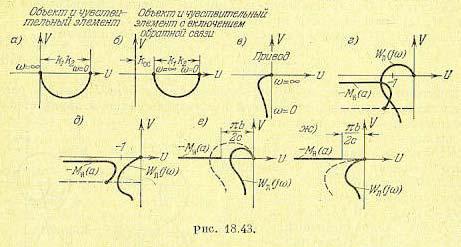
Выражение, стоящее в квадратных скобках (18.220), при kос = 0 (система без обратной связи) соответствует апериодическому звену (регулируемый объект и чувствительный элемент). Оно изображено на рис. 18.43, а. При наличии же жесткой обратной связи в системе ( koc ≠ 0 ) этот график сдвигается вправо на величину kос (рис. 18.43, б).

Множитель перед квадратной скобкой (18.220) соответствует апериодическому интегрирующему звену (привод с регулирующим органом). Он изображен на рис. 18.43, в. Перемножением этих характеристик получаем амплитудно-фазовую характеристику Wл(jw) линейной части системы (в разомкнутом состоянии) соответственно при отсутствии обратной связи (рис. 18.43, г) и при наличии жесткой обратной связи (рис. 18.43, д). Нанесем на эти же графики кривую обратной по величине и по знаку амплитудно-фазовой характеристики — Мн (а) нелинейного звена (в данном случае — реле). Здесь эта кривая изображена в соответствии с рис. 18.39, б для того случая, когда реле характеризуется графиком рис. 18.20, а, причем b2 =b, b1 = mb.

Как видно из рис. 18.43, г, в данном случае в замкнутой системе регулирования без обратной связи возможны автоколебания, так как кривые Wл (jw) и — Мн (а) пересекаются, а введением обратной связи можно уничтожить эти автоколебания (рис. 18.43, д). Очевидно также, что и выбором параметров линейной части системы (т. е. деформацией кривой Wл на рис. 18.43, г) можно было бы уничтожить автоколебания замкнутой нелинейной системы и без обратной связи. Напротив, неудачный выбор параметров может привести к автоколебаниям системы даже и при наличии жесткой обратной связи, если на рис. 18.43, д кривые пересекутся. Чем меньше гистерезисная петля (рис. 18.20, а), тем больше будет т (рис. 18.39) и тем легче, как видно из рис. 18.39, б и рис. 18.43, г, д, сделать замкнутую систему устойчивой.

Когда реле имеет чисто гистерезисную характеристику (рис. 18.20, г), кривая — Мн (а) вырождается согласно рис. 18.39, б (m = -1) в прямую (пунктир на рис. 18.43, д), причем

добиться уничтожения автоколебаний в этом случае нельзя, а можно бороться лишь за уменьшение их амплитуды.

Если в характеристике реле с зоной нечувствительности не будет гистерезисной петли (рис. 18.20, б), то согласно рис. 18.40, а и формуле (18.213) обратная амплитудно-фазовая характеристика нелинейного звена — Мн(а) будет вещественной, как показано на рис. 18.43, е и ж. При этом замкнутая система без обратной связи может иметь автоколебания, если Wл (jw) примет очертание, показанное пунктиром (рис. 18.43, е). Введение же жесткой обратной связи, как видно из рис. 18.43, ж, полностью уничтожает автоколебания.

Из этого предварительного рассмотрения можно сделать вывод, во-первых, о важном стабилизирующем свойстве дополнительной жесткой обратной связи в системе и, вовторых, о стабилизирующем свойстве зоны нечувствительности реле. С точки зрения устойчивости системы выгодно увеличивать и то и другое. Однако эти возможности ограничены из-за увеличения статической ошибки системы при усилении жесткой обратной связи и при увеличении зоны нечувствительности реле. Последнее связано с тем, что система может находиться в состоянии равновесия в любой точке зоны нечувствительности; получается не одно определенное состояние равновесия, а целая область возможных состояний равновесия с разными значениями регулируемой величины.

После сделанных предварительных заключений перейдем к определению амплитуды и частоты автоколебаний в тех случаях, когда последние имеют место.

В случае идеальной релейной характеристики в соответствии с (18.211) и (18.18) имеем

(18.222)

(Мн (а) заполняет всю отрицательную вещественную ось, рис. 18.44, а). Поэтому Wл (jw) при отсутствии жесткой обратной связи (сплошная кривая) пересекает ее, а при наличии жесткой обратной связи не пересекает (пунктирная кривая). В первом случае получаем точку пересечения D, определяющую периодическое решение (ап, wп). Оно будет устойчиво (т. е. соответствует автоколебаниям), так как кривая Wл (jw) охватывает участок прямой — Мн (а) с меньшими амплитудами (линейная часть согласно (18.221) нейтральна, вследствие чего этот критерий можно применять). Во втором же случае кривая Wл(jw) пересекается с прямой — Мн (а) только в точке, где а = 0, w= ∞, т. е. автоколебания отсутствуют (конечная амплитуда получится, если учесть постоянную Т2). Амплитуда ап автоколебаний в первом случае определяется по расстоянию l (рис. 18.44, а) на линии — Мн(а) до точки пересечения, причем с учетом (18.222) получаем

(18.223)

где l берется из графика или вычисляется по формуле

причем величина частоты автоколебаний wп находится из условия

если Uл (wп) и Vл(wп) обозначают вещественную и мнимую части выражения Wл (jw) при kос = 0, т. е.

(18.224)

Отсюда видно, например, что с увеличением передаточного числа регулятора k2k3 увеличивается амплитуда автоколебаний.

Для характеристики реле в виде рис. 18.20, а поведение системы без жесткой обратной связи поясняется рис. 18.44, б. Здесь автоколебания могут отсутствовать (кривая 1 рис. 18.44, б), возможно одно периодическое решение (кривые 2 и 3, пересекающиеся в точке

В) или два периодических решения (кривые 2 и 4, пересекающиеся в точках А и С). При этом кривая 3 соответствует меньшим, а кривая 4 — большим значениям т в релейной характеристике (см. рис. 18.39). Точки В и А отвечают устойчивым автоколебаниям.

Точка С отвечает неустойчивому периодическому процессу, что может означать

устойчивость системы в малом (при а < ас) и стремление к автоколебательному процессу с амплитудой а = аА в большом. Величины амплитуды и частоты автоколебаний определяются по самим кривым в точках их пересечения.

В данном случае влияние величины передаточного числа k2k3 регулятора без жесткой обратной связи заключается в том, что с увеличением k2k3 осуществляется переход от кривой 1 к кривой 2 (рис. 18.44, б), т. е. автоколебания в системе появляются только тогда, когда передаточное число k2k3 превзойдет некоторое граничное значение, определяемое моментом касания кривой 1 с кривой 3 или 4.

Аналогично определяются автоколебания и при наличии жесткой обратной связи, как показано на рис. 18.44, в.

Наконец, при чисто гистерезисной характеристике реле получаем только автоколебательный процесс (рис. 18.44, г), амплитуда и частота которого без жесткой обратной связи определяются точкой Е, а при наличии жесткой обратной связи - точкойН. Во всех рассмотренных случаях, как и вообще в рассматриваемом частотном методе, через ап обозначается амплитуда автоколебаний входной величины нелинейного звена, т. е. в данном случае величины х. Чтобы определить амплитуду aθ автоколебаний

регулируемой величины θ (температуры), надо найти передаточную функцию, связывающую величины х и θ :

и следовательно,

Для системы без обратной связи (koc = 0)

Аналогично можно определить амплитуду первой гармоники автоколебаний для других переменных в данном системе.

Учет временного запаздывания в реле. В рассмотренном выше примере системы автоматического регулирования температуры, считалось, что в характеристике реле рис. 18.20 величины b1; b2, b заданы постоянными, т. е. считалось, что характеристики реле

имеют обычный гистерезисный вид с заданным по входной координате отставанием в срабатывании реле. Теперь же будем считать, что имеются данные запаздывания во времени срабатывания и отпускания реле (одинаковые). Такое нелинейное звено с запаздыванием можно разбить на два элемента: 1) обычное нелинейное звено, характеризующееся графиком рис. 18.45, б или в, и 2) элемент запаздывания (рис. 18.45, а), описываемый уравнением

Тогда можно будет записать выражение амплитудно-фазовой характеристики линейной части системы вместе с элементом запаздывания в виде

(18.225)

Правило построения такой характеристики описано в главе 14.

Пусть реле (после выделения элемента запаздывания) характеризуется графиком рис. 18.45, б. В этом случае для системы с жесткой обратной связью получим соответственно кривые Wл (jw) и Wлз(jw), изображенные на рис. 18.45, г, а также прямую — Мн (а) на основании формулы (18.213) ирис. 18.40, а. Если кривые Wлз(jw) и — Мн(а) пересекаются, то будут иметь место автоколебания. Но, как видно из рис. 18.45, г, при достаточно малых запаздываниях т указанные кривые могут не пересекаться, т. е. автоколебаний не будет.

Здесь, как и в линейных системах, можно определить критическое время запаздывания, до которого автоколебания отсутствуют, без построения кривой Wлз(jw), а только по кривым Wл(jw) и — Мн(а). В самом деле, в критическом случае некоторая точка кривой WЛЗ (jw) попадет в крайнюю точку B (рис. 18.45, г). Это, как видно из чертежа, соответствует такой точке К кривой Wл (jw), в которой

(18.226)

Из первого условия определяется величина wk из второго — критическое время запаздывания:

(18.227)

Такое решение можно найти непосредственно из графика WЛ (jw) или же аналитически, используя выражение (18.220).

Если же реле не имеет зоны нечувствительности, т. е. b= 0, то точка В попадет в начало координат на рис. 18.45, г и автоколебания будут при любом значении времени запаздывания в срабатывании реле (τk = 0). Поэтому выгодно, чтобы временное

запаздывание в реле, рассматриваемое здесь, было бы сравнительно малым, а зона

нечувствительности имела бы большую величину (но не превышала допустимых значений, полученных из статического расчета точности регулирования).

Амплитуда и частота автоколебаний при наличии запаздывания определяются следующие образом. Точка пересечения D(рис. 18.45, г) дает два периодических решения, так как в ней на прямой — Мн (а) имеются два значения а. Это следует из графика рис. 18.40, а, причем на основании (18.16) имеем

(18.228)

что изображается графиком рис. 18.45, д. Расстоянию от начала координат l точки пересечения D на рис. 18.45, г соответствуют две точки графика D1 и D2 на рис. 18.45, д, которые дают два значения амплитуды: ап1 и ап2. Частота wп обоих периодических решений одинакова и определяется точкой D на кривой Wлз (jw).

При этом периодическое решение с меньшей амплитудой ап1 будет неустойчивым, а с большей амплитудой aп2 — устойчивым, так как в первом случае точка с положительным приращением ∆а на линии — Мн(а) охватывается кривой Wлз(jw), а во втором случае — не охватывается. Следовательно, могут иметь место устойчивость системы в малом (до амплитуд ап1) и автоколебательный процесс с большой амплитудой, к которому стремится система при начальных амплитудах переходного процесса, превышающих значение aп1. Заметим, что точку пересечения D кривой Wлз (jw) с линией — Мн(а) можно найти без построения кривой Wлз (jw) непосредственно по амплитудно-фазовой характеристике Wл(jw) линейной части системы без элемента запаздывания. Для этого нужно на кривой Wл(jw) найти такую точку wп (рис. 18.45, г), которая бы при повороте вектора Ал на угол τwп попала на линию — Мн (а), что и даст нам точку D(величина запаздывания τ задана,

wп неизвестна). Условие для определения wп будет

после этого находится величина l= Ал затем амплитуда автоколебаний ап2 по графику рис. 18.45, д.

Вданном параграфе применялись амплитудно-фазовые частотные характеристики. Использование логарифмических частотных характеристик см. в § 20.4.

Взаключение заметим, что при исследовании нелинейных автоматических систем применяются еще приближенные методы Б. В. Булгакова (см. [19] или [98]), которые здесь не излагаются.

Г Л А В А 19

МЕДЛЕННО МЕНЯЮЩИЕСЯ ПРОЦЕССЫ В АВТОКОЛЕБАТЕЛЬНЫХ СИСТЕМАХ

§19.1. Статические и скоростные ошибки автоколебательных систем

Впредыдущих главах исследовались симметричные автоколебания как результат свободного движения системы (т. е. без внешнего воздействия) при симметричных нелинейностях. Однако, как будет показано, важное практическое значение имеет также рассмотрение несимметричных автоколебаний.

Несимметрия автоколебаний может вызываться различными причинами:

1) несимметричностью нелинейной характеристики как при наличии, так и при отсутствии внешних воздействий:

2)наличием постоянного или медленно меняющегося внешнего воздействия при симметричных нелинейностях; 3) наличием постоянной или медленно меняющейся скорости изменения внешнего

воздействия при симметричных нелинейностях (для тех случаев, когда постоянное воздействие не вызывает смещения центра колебаний; обычно это имеет место в следящих системах и вообще в астатических системах).

В самом деле, если имеется несимметричная нелинейная характеристика (например, рис. 19.1, а, б), то даже при симметричных колебаниях переменной х = аsinwt (возникают несимметричные по амплитуде колебания переменной F (рис. 19.1, б). Если же нелинейность симметрична (например, рис. 19.2, а, б), то при наличии постоянного внешнего воздействия (или в астатических системах при наличии постоянной скорости

изменения внешнего воздействия) смещается центр колебаний переменной х = х° +а sinwt, вследствие чего колебания переменной F становятся несимметричными по амплитуде и по времени (рис. 19.2, а) или только по времени (рис. 19.2, 6).

Пусть задана автоматическая система, динамика которой описывается уравнением

(19.1)

В данном параграфе будем считать f(t) = const =f ° для статических систем или же pf(t)=const =f° для астатических систем. Астатической системой называется такая, в которой многочлен S(р) имеет общий множитель р, т. е. S(р) = pS1(р).

Поэтому запишем уравнение (19.1) в виде

(19.2)

где соответственно

(19.3)

При этом решение нелинейного уравнения (19.1), в отличие от прежнего (§ 18.2), ищется в форме

(19.4)

причем х°, а, w являются неизвестными постоянными.

С учетом величины смещения х° первые члены разложения в ряд Фурье вместо (18.6) и (18.7) следует записать в виде

(19.5)

где при обозначении ψ = wt

(19.6)

Отсюда видно, что в общем случае все три коэффициента являются функциями трех неизвестных:

(19.7)

В частных случаях эти зависимости могут быть более простыми.

Подстановка выражений (19.4) и (19.5) в заданное дифференциальное уравнение (19.1) с учетом свойства фильтра (см. § 18.2) дает

Это уравнение разбивается на два: (19.8)

(19.9)

При таком разделении сохраняются существенно нелинейные свойства и отсутствие суперпозиции решений, так как остается нелинейная взаимосвязь обоих уравнений через соотношения (19.7).

Можно предложить два метода решения задачи.

Первый метод состоит в следующем. Уравнение (19.9) совпадает с прежним уравнением (18.33); отличие состоит лишь в том, что теперь коэффициенты q и q' согласно (19.7) зависят не только от а и w, но и от смещения х°. Поэтому, написав как прежде, характеристическое уравнение

(19.10)

заменив р на jw и выделив вещественную и мнимую части, в отличие от (18.36), получим здесь два алгебраических уравнения с тремя неизвестными:

(19.11)

Эти уравнения дают возможность определить амплитуду ап и частоту wп автоколебаний как функции постоянной составляющей х°:

(19.12)

Для решения этой задачи можно применять любой из способов, описанных в § 18.2, в зависимости от того, какой из них лучше подходит к условиям заданной конкретной задачи. Таким же способом можно определить зависимость а и w не только от х°, но и от параметров системы с целью выбора последних. Что касается тех способов § 18.2, где используются графики q(а) и q'(а), то здесь их необходимо строить в виде серии кривых при разных постоянных значениях х° (рис. 19.3).

После того как из уравнений (19.11) определены зависимости (19.12), можно, воспользовавшись первым из выражений (19.7), найти функцию смещения

(19.13)

Подставив ее в (19.8), получим алгебраическое уравнение

(19.14)

с одной неизвестной х°, которая отсюда и определяется. Чаще всего это уравнение относительно х° является трансцендентным и решается графически. Затем согласно (19.12) определяются также амплитуда ап и частота wп.

См. конкретные формулы для разных нелинейностей в § 19.3.

Указанную зависимость (19.12) амплитуды и частоты автоколебаний от величины смещения центра колебаний, характерную именно для нелинейных систем (в линейных системах смещение центра колебаний не играет роли), надо всегда иметь в виду. При одних нелинейностях она может быть весьма существенной, при других — менее существенной.

Второй метод решения той же задачи состоит, наоборот, в том, что сначала решается уравнение (19.8), где согласно (19.7) будет F° (х°, а, w) или часто F° (х°, а). Решение получает вид

(19.15)

Это решение подставляется затем в уравнения (19.11), которые, таким образом, будут содержать только две неизвестные: ап и wп. Определив последние (по любому из способов