Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975

где а = 0,05, β = 1,35, w12 = 7,5, ϕ = 0,03. Меняя величину дисперсии помехи σ f2,

характеризующую «уровень помехи», будем определять динамические качества системы в зависимости от величины σ f.

Произведя статистическую линеаризацию (22.3), разобьем уравнение системы (22.36) на два, соответственно для регулярной и случайной составляющих:

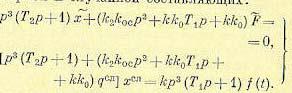(22.38)

Поскольку передаточная функция линейной части системы

при заданных выше ее параметрах практически не пропускает частот, при

которых спектральная плотность помехи (рис. 22.11) имеет существенное значение, то согласно (22.31) дисперсия помехи на входе нелинейного звена будет

Чтобы привести этот интеграл к стандартному виду (§ 11.6), преобразуем сначала знаменатель спектральной плотности, а именно:

Тогда согласно обозначениям приложения 2 получим

где

Вчислителе же получим

Врезультате находим

(22.39)

где согласно приложению 2

(22.40)

Перейдем теперь к уравнению (22.38) для регулярной составляющей, т. е. для полезного сигнала х. Функция F определяется в нем графиком рис. 22.6, б в зависимости от х1 =x/b и σ 1 = σ x/b . В начальной части все кривые этого графика близки к прямым. Поэтому можно провести их обычную линеаризацию в виде

(22.41)

где kн— крутизна в начале координат (рис. 22.6, б), которая зависит от величины σ 1. Для данной задачи получим

Физически величина kн является коэффициентом усиления полезного» сигнала в нелинейном звене в присутствии помех, причем приведенная таблица дает зависимость этого коэффициента от уровня помехи, т. е. от среднеквадратичного ее значения σ 1= σ x/b, на входе нелинейного звена.

Как видим, увеличение уровня помехи ведет к существенному снижению коэффициента усиления полезного сигнала в нелинейном звене, что показано графически на рис. 22.12. Это составляет принципиальную особенность нелинейной системы, которая обусловливает зависимость всех ее статических и динамических качеств по полезному сигналу, в том числе и устойчивости, от уровня помех.

Найдем, например, зависимость устойчивости системы от уровня помех. Для этого согласно (22.38) и (22.41) запишем характеристическое уравнение системы;

(22.42)

Условие устойчивости системы по критерию Гурвица принимает вид

(22.43)

При заданных в начале параграфа параметрах это дает kн>1,17. Это согласно рис. 22.12 соответствует значению

Но согласно (22.39)

(22.44)

где обозначено

Эту величину удобно принять для выражения среднеквадратичного значения внешней помехи σ f в относительных единицах, учитывая, что согласно рис. 22.10 размерности переменных f(t) и х связаны между собой именно через коэффициент k= k1k2.

Вычислив величину I3 по формуле (22.40) при заданных выше параметрах системы, из

(22.44) находим

Это означает, что только при уровне помех, не превышающем указанного значения, данная система остается устойчивой. Далее она теряет устойчивость по полезному сигналу.

Выясним теперь влияние параметров k и Т1 на устойчивость системы в присутствии помех. Для этого по формуле (22.43) найдем сначала границы устойчивости системы на плоскостях параметров k, kн и Т1, kн (рис. 22.13, а и б). На границе устойчивости для

каждого значения kн по графику рис. 22.12 (или по приведенной выше таблице) находим величину k, а по ней согласно (22.44) и среднеквадратичное значение внешней помехи, при которой теряется устойчивость системы;

(22.45)

Это позволяет перестроить найденные на рис. 22.13 границы устойчивости в новые координаты соответственно

(рис. 22.14, а и б). При этом надо иметь в виду, что величина I3, согласно (22.40), зависит от параметра Т1, вследствие чего вычисление по формуле (22.45) при построении графика рис. 22.14, б необходимо производить с учетом изменения I3 при изменении Т1.

Как видим, с увеличением параметра k опасный уровень помех снижается, а при увеличении параметра Т1 он растет. Это вполне естественно, поскольку Т1 является, согласно рис. 22.10, коэффициентом интенсивности введения производной, улучшающим стабилизацию системы.

По линейному уравнению, вытекающему из (22.38) и (22.41),

используя линейную теорию автоматического регулирования, можно исследовать также и все другие динамические качества данной нелинейной системы по полезному сигналу в присутствии помех, учитывая, однако, при этом все время, что величина коэффициента kн зависит от уровня помех σ f, от общей структуры и от некоторых параметров системы.

ГЛАВА 23 НЕЛИНЕЙНАЯ ОПТИМИЗАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

§ 23.1. Общие положения

Ранее, в главе 12, была рассмотрена уже задача оптимизации систем автоматического регулирования в линейной постановке. Однако в большинстве случаев практики, когда на управление накладываются ограничения по величине, по скорости или другие, оптимальный закон регулирования становится нелинейным, если даже сам регулируемый объект описывается линейными уравнениями. Тогда система в целом после оптимизации становится нелинейной.

Итак, здесь будет рассматриваться синтез такого закона регулирования, который оптимизирует процесс управления в системе по заданному критерию, причем этот закон регулирования оказывается нелинейным:

(23.1)

Оптимизации может подвергаться также и временная программа управления. Наиболее простой является задача оптимизации системы регулирования по быстродействию, т. е. по минимуму времени переходного процесса при заданных начальных отклонениях и при отсутствии внешнего воздействия. Усложнение задачи возникает при усложнении критерия оптимизации в виде минимума функционала

(23.2)

или же при усложнении ограничений, задаваемых в виде неравенств

(23.3)

а также при повышении порядка уравнений системы и при наличии внешних воздействий. Внешние воздействия и начальные условия могут быть заданы в детерминированной форме или же вероятностными характеристиками.

Существуют различные методы оптимизации процессов управления и регулирования. Ниже будет в простейшем виде изложено использование принципа максимума Л. С. Понтрягина [96], а затем последовательная оптимизация на базе нелинейного программирования, разработанная В. М. Пономаревым [105]. Другие важные направления развиты в работах Н. Н. Красовского [63] и др., ранее уже рассматривались работы А. М. Летова [77] и принцип динамического программирования Р. Беллмана [5]; см. также книги

[60, 95, 133].

§ 23,2. Синтез оптимальной системы с использованием принципа максимума

Принцип максимума, используемый в теории (оптимальных систем, разработан школой Л. С. Понтрягина [96].

Допустим, что уравнения динамики системы автоматического регулирования заданы в следующей общей форме (нелинейной):

(23.4)

(без переменных во времени коэффициентов и без внешнего воздействия), где x1, х2, ..., хn — переменные, относящиеся к заданной части системы, включающей в себя регулируемый объект и не изменяемую в процессе синтеза часть регулятора; u1, u2,..., иm—переменные, выражающие воздействия проектируемой части регулятора на заданную часть системы и называемые коротко управлениями. Неизменяемой частью регулятора может быть, например, его силовая часть (привод регулирующего органа);

тогда u1, . . ., ur будут воздействиями измерительно-преобразовательной части регулятора на его силовую часть (рис. 23.1).

В заданные уравнения системы (23.4) не входят уравнения проектируемой преобразовательной части регулятора, которые должны быть найдены в процессе синтеза в виде зависимостей (закон регулирования)

(23.5)

Во всякой реальной системе величины управлений uj будут ограниченными, например,

или любой другой определенной областью допустимых значений.

Критерием оптимальности системы пусть будет минимум некоторого функционала

(23.6)

Для удобства решения задачи вводится дополнительная искусственная переменная х0 (t), определяемая уравнением

(23.7)

а также еще вспомогательные переменные ψ 0, линейными однородными уравнениями

(23.8)

Если ввести теперь вспомогательную функцию Н в виде

(23.9)

то все уравнения (23.4), (23.7) и (23.8) можно объединить в одну систему, типа известной из механики системы уравнений Гамильтона, а именно;

(23.10)

(23.11)

Принцип максимума гласит, что для оптимальности системы, т. е. для получения минимума функционала I(23.6), необходимо существование таких ненулевых непрерывных функций ψ 0 (t), . . ., ψ n(t), что при любом I, находящемся в заданном

интервале t0<t<t1, величина Н, как функция переменных u1, . . ., ur, в заданной области их допустимых значений достигает максимума

(23.12)

причем ψ 0 и M -постоянны во времени и

(23.13)

Для простейшего случая оптимальности — оптимальности по быстродействию — имеем fо = 1, а функция Н принимает вид

где

(23.14)

В этом случае прежние искусственные величины с нулевыми индексами не нужны. Гамильтонова система уравнений принимает вид

(23.15)

(23.16)

Формулировка принципа максимума: для оптимальности системы по быстродействию необходимо существование таких ненулевых непрерывных функций ψ 1 (t), . . ., ψ n(t), что

для всех 2 в заданном интервале t0<t<t1. функция Н переменных u1, . . ., un в заданной области их допустимых значений достигает максимума:

(23.17)

причем величина М постоянна во времени и

(23.18)

Согласно приведенным формулировкам принцип максимума дает только необходимые условия оптимальности. Вопрос же о существовании ее и о случаях достаточности этих условий очень труден. Поэтому в практических приложениях заранее интуитивно предполагают достаточность по физическому смыслу исследуемой системы. Применение принципа максимума проиллюстрируем сначала на двух простейших примерах, когда решение задачи доводится до конца в аналитической форме [96]. Пример 1. Система задана уравнением

(23.19)

Требуется найти уравнение преобразовательной части системы u = u(х), чтобы система была оптимальной по быстродействию при переходе ее из произвольного начального

состояния в равновесное состояние (х = 0, dxdt = 0) . При этом на управление u наложено ограничение

Обозначив х1 = x, dxdt = x2, приведем уравнение (23.19) к исходному виду (23.4):

(23.20)

Функция Н согласно (23.14) и (23.4) здесь имеет вид

(23.21)

Чтобы определить максимум по переменной u, надо найти ψ 2. Для этого воспользуемся уравнениями (23.16), которые в данном случае будут

x20) процесс идет по некоторой параболе М0D при управляющем сигнале u = -1 (в другой области было бы u = +1). В точке D происходит переключение реле на сигнал u = -1, после чего процесс идет по параболе ОD и заканчивается в точке О за конечное время, которое согласно принципу максимума является минимальным :из всех возможных для перехода данной системы из состояния М0 (х10, х20) в равновесное состояние О (0, 0).

Точка переключения реле D может находиться в любом месте кривой АОВ. Последняя называется поэтому линией переключения. На ней лежат заключительные отрезки фазовых траекторий, приходящие в начало координат.

Итак, искомое уравнение преобразовательной части системы (оптимальной по быстродействию) будет

(23.24)

причем х = х1 отсчитывается на оси абсцисс. Замечая, что из формул (23.22), (23.23) и рис. 23.2 находим уравнение линии переключения:

(23.25)

и следовательно, уравнение преобразовательной части системы будет

(23.26)

Итак, в системе должны быть либо два измерителя, либо один измеритель х и дифференцирующее устройство. Должно формироваться (автоматически вычисляться) переключающее значение согласно формуле (23.25), и на основе сравнения фактического текущего значения со значением зависящим от текущего х, должно производиться включение и переключение реле в соответствии с уравнением (23.26).

Это является специальным нелинейным законом регулирования для линейного объекта (23.19), приводящим к оптимальной по быстродействию системе. Таков результат решения простейшей задачи оптимизации.

Пример 2. Пусть задана система

(23.27)

Требуется найти такое уравнение преобразовательной части системы u = u(х), чтобы система была оптимальной по быстродействию, т. е. в кратчайшее время приходила бы в

равновесное состояние х = 0, dxdt = 0. При этом задана область допустимых значений управления

Перепишем заданное уравнение (23.27) в виде

(23.28)

Функция Н согласно (23.14) и (23.4) здесь будет

(23.29)

Для вспомогательных переменных из (23.16) и (23.29) получаем уравнения

откуда