Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975

ГЛАВА 18

ПРИБЛИЖЕННЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ И АВТОКОЛЕБАНИЙ

§18.1. Гармоническая линеаризация нелинейностей

Вэтой главе будет изложен метод гармонической линеаризации для приближенного определения периодических решений (автоколебаний) и устойчивости нелинейных систем любого порядка, который по идее близок к методу эквивалентной линеаризации или методу гармонического баланса Н. М. Крылова и Н. Н. Боголюбова, а по результатам — также и к методу малого параметра Б. В. Булгакова.

Рассматриваемый приближенный метод является мощным средством исследования нелинейных автоматических систем в смысле простоты и довольно большой универсальности его аппарата в применении к самым разнообразным нелинейностям. Однако надо иметь в виду, что он решает задачу приближенно. Имеются определенные ограничения его применимости, о которых будет сказано ниже. Эти ограничения обычно хорошо соблюдаются в задачах теории автоматического регулирования. Практические расчеты и эксперимент показывают приемлемость этого метода для многих видов нелинейных систем.

Пусть дано какое-нибудь нелинейное выражение вида

(18.1)

и задано

(18.2)

Тогда

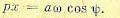(18.3)

Разложив функцию в правой части выражения (18.1) в ряд Фурье, получим

(18.4)

Положим

(18.5)

что означает отсутствие постоянной составляющей в данном разложении. В настоящей главе будет везде предполагаться выполнение условия отсутствия постоянной составляющей (18.5). Впоследствии (глава 19) будет дан метод исследования автоколебаний при наличии постоянной составляющей, т. е. в случае невыполнения условия (18.5).

Если принять во внимание, что из (18.2) и (18.3)

то формулу (18.4) при условии (18.5) можно будет записать в виде

(18.6)

где q и q' — коэффициенты гармонической линеаризации, определяемые формулами:

(18.7),

Итак, нелинейное выражение (18.1) при х = а sinwt заменяется выражением (18.6), которое с точностью до высших гармоник аналогично линейному. Эта операция и называется гармонической линеаризацией. Коэффициенты q(а, w) и q'(а, w) постоянны при постоянных значениях а и со, т. е. в случае периодического процесса. В переходном колебательном процессе с изменением а и w коэффициенты q и q' изменяются (см. гл. 20). Для разных амплитуд и частот периодических процессов коэффициенты выражения (18.6) будут различны по величине. Это очень важное для дальнейшего обстоятельство является существенным отличием гармонической линеаризации, по сравнению с обычным способом линеаризации (§ 3.1), приводящим к чисто линейным выражениям, которые применялись в предыдущих разделах книги. Указанное обстоятельство и позволит путем применения к выражению (18.6) линейных методов исследования проанализировать основные свойства нелинейных систем, которые не могут быть обнаружены при обычной линеаризации.

Приведем также формулы гармонической линеаризации для более простой нелинейности:

следующим выражением (при x=asinwt):

(18.9).

где

(18,10)

при условии отсутствия постоянной составляющей

Если же кривая F(х) не имеет гистерезисной петли, то q' = 0, так как при х =asinwt будет

(при гистерезисной петле этот интеграл не был нулем вследствие различия в очертании кривой F(х) при возрастании и убывании х).

Следовательно, при отсутствии гистерезисной петли нелинейное выражение (18.8) заменяется более простым:

Как видим, звено с зоной нечувствительности уподобляется здесь линейному звену с уменьшенным за ее счет коэффициентом усиления. Это уменьшение коэффициента усиления значительно при малых амплитудах и невелико при больших, причем

0 ≤ q(a) ≤ k приb ≤ a ≤ ∞.

Для второго частного случая — звено с насыщением без зоны нечувствительности (рис. 18.2, г),— полагая b1 = 0, т. е. ψ1 = 0, из (18.20) и (18 19) получаем

(18.22)

причем при a ≤ kc имеем q= k (линейная характеристика) . При амплитудах колебания

входной величины, захватывающих зону насыщения, данное звено заменяется как бы линейным звеном с тем меньшим коэффициентом усиления q(а), чем больше амплитуда (в противоположность предыдущему).

Для звена с переменным коэффициентом усиления согласно рис. 18.2, д и е по формуле (18.10) с учетом (18.12) получаем

что с заменой sinψ1 = b дает

(18.23)

Здесь ломаная характеристика (рис. 18.2, д) заменяется одной прямой со средним между k1 и k2 наклоном q(а), причем этот наклон изменяется в интервале k1 ≤ q(a) ≤ k2 при

увеличении амплитуды b ≤ a ≤ ∞ . Для амплитуд а < b имеем линейную характеристику с наклоном k1.

Для нелинейного звена с насыщением и с гистерезисной петлей (рис. 18.3, а) уравнение получит уже вид (18.9), где согласно рис. 18.3, б и формулам (18.10)

аналогично и для q'(а). Отсюда

(18.24)

где

(18.25)

Если в таком нелинейном звене амплитуда колебаний входной величины х1 будет а < b, то в процессе колебаний не будет захватываться зона насыщения и получится чисто гистерезисная характеристика (рис. 18.3, в). В данном случае

(18.26)

Уравнение звена с гистерезисной характеристикой вида рис. 18.3, в поэтому будет иметь форму (18.9), где согласно (18.24)

(18.27)

Величина ψ1 вычисляется по формуле (18.26).

Такого же типа характеристика (рис. 18.3, в) получалась и для чувствительного элемента с сухим трением в системе регулирования давления, рассмотренной в § 16 (см. рис. 16.21, б), когда мы пренебрегали массой. Следовательно, для такого нелинейного звена с сухим трением будут справедливы те же формулы (18.27) с заменой в них только

(18.28)

а уравнение (16.58) для колебательного процесса в форме (18.9) будет

(18.29)

Этого же типа характеристика (рис. 18.3, в) имела место и для нелинейного звена с зазором в следящей системе (см. рис. 16.20, б), причем там k = 1. Следовательно, уравнение (16.55) данного нелинейного звена (для колебательного процесса) запишется в виде

(18.30)

где q(а) и q' (а) определяются по формулам (18.27), в которых надо считать k = 1.

Для нелинейностей, не заданных аналитически, существует графический способ определения д (а) (см. § 3.8 в книге [100]).

§ 18.2. Алгебраические способы определения автоколебаний и устойчивости в нелинейных системах первого класса

Основываясь на вышеизложенной гармонической линеаризации, составим гармонически линеаризованное уравнение всей замкнутой нелинейной автоматической системы в целом (рис. 16.1). Пусть известно дифференциальное уравнение линейной части системы

(18.31)

причем линейная часть может иметь структуру любой сложности (и любой порядок уравнения).

Уравнение нелинейного звена

в колебательном процессе после гармонической линеаризации запишем в виде

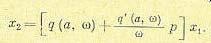(18.32)

В частности, для нелинейной характеристики х2=F(x1) ной петли будет

Уравнение нелинейного звена (18.32) записано, как видим, без учета высших гармоник, фигурировавших в предыдущем параграфе. Это сделано отнюдь не потому, что они малы. В отдельно взятом нелинейном звене при подаче на вход x1=sinwt в общем случае на выходе обязательно появятся высшие гармоники. Однако в замкнутой автоматической системе (рис. 18.4, а) линейная часть имеет обычно амплитудную частотную

характеристику одного из двух видов, показанных на рис. 18.4, б. Поэтому высшие гармоники, имеющиеся у переменной а;2, гасятся в линейной части и переменная х2 оказывается достаточно близкой к синусоиде; x1 = аsinwt. В таком виде и будем искать приближенное периодическое решение для нелинейной автоматической системы. Свойство линейной части системы, определяющее вид амплитудной частотной характеристики типа изображенной на рис. 18.4, б, именуется свойством фильтра. Аналитическое обоснование сказанного см. в книге [100, § 2.2].

Как видим, в коэффициенты уравнения (18.32) входят амплитуда а и частота w искомого колебательного процесса.

На основании уравнений (18.31) и (18.32) можно написать гармонически линеаризованное характеристическое уравнение замкнутой нелинейной системы в виде

(18.33)

с теми же особенностями в коэффициентах, что и в уравнении (18.6), описанными в § 18.1. В том случае, когда в замкнутой системе возникают собственные незатухающие колебания постоянной амплитуды а = ап и постоянной частоты w = wп (автоколебания),

коэффициенты уравнения (18.32), а значит, и коэффициенты характеристического уравнения (18.33), становятся постоянными. Вместе с тем из линейной теории известно, что появление указанных колебаний в системе при постоянных коэффициентах соответствует наличию пары чисто мнимых корней в характеристическом уравнении системы.

Следовательно, можно обнаружить в замкнутой нелинейной системе появление незатухающих собственных колебаний вида х≈ап sinwt(ап = const, w = const), подставив в характеристическое уравнение (18.33) Р = jwп. Если эта подстановка р = jwп соответствует каким-нибудь вещественным положительным значениям а =ап и w = wп при заданных параметрах системы, то такие колебания возможны. Но подстановка р =jwп в характеристическое уравнение с постоянными коэффициентами эквивалентна отысканию границы устойчивости линейной системы. Следовательно, появление незатухающих собственных колебаний в нелинейной системе можно обнаружить применением к характеристическому уравнению (18.33) любого из методов определения границы устойчивости линейной системы, изложенных в главе 6.

Основной способ определения периодических решений. Используем непосредственную подстановку р = jw в гармонически линеаризованное характеристическое уравнение, а именно

(18.34)

яри неизвестных постоянных значениях амплитуды а и частоты w, входящих в коэффициенты q и q', причем для однозначной нелинейной характеристики F(x1) будет

Выделим в выражении (18.34) вещественную и мнимую части:

(18.35)

и введем для частоты и амплитуды искомого периодического решения обозначения: w=wп, а = aп. Это дает два уравнения

(18.36)

из которых и определяются неизвестные частота wп и амплитуда ап.

Если уравнения (18.36) не имеют положительных вещественных решений для ап и wп, то периодические решения вообще (а значит, и автоколебания) в данной нелинейной системе невозможны.

Исследование устойчивости периодического решения дается ниже.

С помощью уравнений (18.36) можно не только определять частоту wп и амплитуду ап автоколебаний при заданных параметрах системы, но и построить графики зависимостей wп и ап от какого-либо параметра системы, например коэффициента усиления k. Для этого нужно считать в уравнениях (18.36) параметр k переменным и записывать эти уравнения в виде

(18.37)

Отсюда можно найти зависимости

и построить их, например, в виде графиков рис. 18.5, а, б. На основании этих трафиков можно будет выбирать параметр k так, чтобы амплитуда автоколебаний была достаточно малой, чтобы частота их не была опасной для данной системы или же, наконец, чтобы автоколебаний не было вовсе.

Кроме того, с помощью тех же уравнений (18.36) можно строить линии .равных значений амплитуды и частоты автоколебаний на плоскости двух каких-либо параметров системы, например k и Т . Для этого уравнения (18.36) записываются в виде

(18.38)

Зададимся различными числовыми значениями амплитуды ап и получим для каждого из них по уравнениям (18.38) зависимости

После этого, меняя wп, можно построить по точкам соответствующие кривые ап = const; в координатах (k, T), как показано сплошными линиями на рис. 18.5, в. На этих кривых получаются отметки частот wп, которые также можно соединить (пунктирные кривые).

График рис. 18.5, в позволяет выбирать, значения двух параметров (k и Т) нелинейной системы. Если такие графики построить, для различных возможных структурных схем системы, то можно будет выбирать, также и наивыгоднейшую структурную схему проектируемой замкнутой автоматической системы с учетом нелинейностей.

Использование графиков коэффициентов гармонической линеаризации. Во многих задачах коэффициенты q и q', входящие в уравнение (18.34), сложно зависят от амплитуды а, а в ряде случаев и от частоты w. В таких случаях удобнее указанное уравнение записывать в виде

(18.39)

не подставляя зависимости q и q' от а и w. Тогда вместо уравнений (18.36) получим для определения периодического решения уравнения:

(18.40)

Для общего случая задач, в которых каждый из коэффициентов гармонической линеаризации q и q' зависит сложным образом от обеих неизвестных а и w, т. е.

(18.41)

можно применить следующий прием решения. Задаваясь различными значениями а и со, построим по формулам (18.41) две серии кривых: q(w) и q' (w) при разных а = const; (рис. 18.6). Затем из уравнений (18.40) выразим