Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975

ГЛАВА 14 СИСТЕМЫ С ЗАПАЗДЫВАНИЕМ И СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ

ПАРАМЕТРАМИ

§ 14.1. Уравнения линейных систем с запаздыванием

Линейными системами с запаздыванием называются такие автоматические системы, которые, имея в общем ту же самую структуру, что и обыкновенные линейные системы (раздел II), отличаются от последних тем, что в одном или нескольких из своих звеньев имеют запаздывание во времени начала изменения выходной величины (после начала изменения входной) на величину т, называемую временем запаздывания, причем это время запаздывания остается постоянным и во всем последующем ходе процесса. Например, если обыкновенное линейное звено описывается уравнением

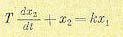(14.1)

(апериодическое звено первого порядка), то уравнение соответствующего линейного звена с запаздыванием будет иметь вид

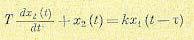(14.2)

(апериодическое звено первого порядка с запаздыванием). Такого вида уравнения называются уравнениями с запаздывающим аргументом или дифференциальноразностными уравнениями.

Обозначим х*(t) = х1(t -τ ). Тогда уравнение (14.2) запишется в обыкновенном виде:

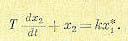(14.3)

Так, если входная величина х1 изменяется скачком от нуля до единицы (рис. 14.1, а), то

переходную характеристику обыкновенного апериодического звена в применении к уравнению (14.3), получаем изменение выходной величины х2 в виде графика рис. 14.1, в. Это и будет переходная характеристика апериодического звена первого порядка с запаздыванием (его апериодическое «инерционное» свойство определяется постоянной времени Т, а запаздывание — величиной τ ).

Линейное звено с запаздыванием. В общем случае, как и для (14.2), уравнение динамики любого линейного звена с запаздыванием можно разбить на два:

(14.4)

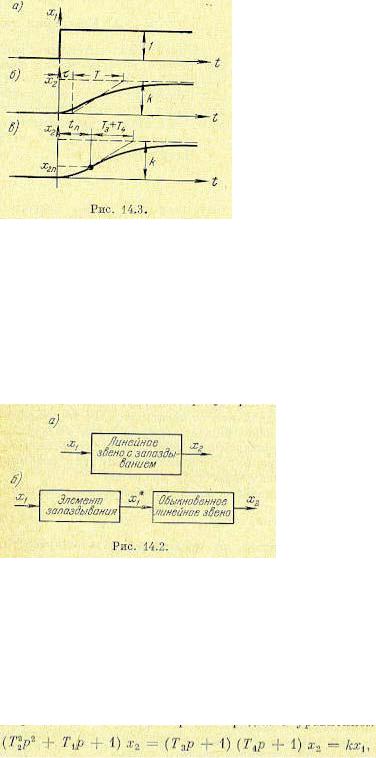
что соответствует условной разбивке линейного звена с запаздыванием (рис. 14.2, а) на два: обыкновенное линейное звено того же порядка и с теми же коэффициентами и предшествующий ему элемент запаздывания (рис. 14.2, б).

Временная характеристика любого звена с запаздыванием будет, следовательно, такая же, как у соответствующего обыкновенного звена, но только сдвинута по оси времени вправо на величину τ .

Примером звена «чистого» запаздывания т является акустическая линия связи (τ — время прохождения звука). Другими примерами могут служить система автоматического дозирования какого-либо вещества, перемещаемого с помощью ленточного транспортера (τ — время движения ленты на определенном участке), а также система регулирования толщины прокатываемого металла, где т означает время движения металла от валков до измерителя толщины. В двух последних примерах величина т называется транспортным запаздыванием.

В первом приближении определенной величиной запаздывания т могут быть охарактеризованы трубопроводы или длинные электрические линии, входящие в звенья системы (подробнее о них см. § 14.2).

Величину запаздывания τ в звене можно определить экспериментально путем снятия временной характеристики. Например, если при подаче на вход звена скачком некоторой величины, принимаемой за единицу, на выходе получается экспериментальная кривая для x2, показанная на рис. 14.3, б, то можно приближенно описать это звено как апериодическое звено первого порядка с запаздыванием (14.2), взяв величины τ , Т и k экспериментальной кривой (рис. 14.3, б).

Заметим также, что такая же экспериментальная кривая согласно графику рис. 14.3, в может трактоваться и как временная характеристика обыкновенного апериодического звена второго порядка с уравнением

причем T1, Т2 и k можно вычислить из соотношений, записанных в § 4.5 для данного звена, по некоторым замерам на экспериментальной кривой или другими способами. Итак, с точки зрения временной характеристики реальное звено, приближенно описываемое уравнением первого порядка с запаздывающим аргументом (14.2), часто может быть с такой же степенью приближения описано обыкновенным

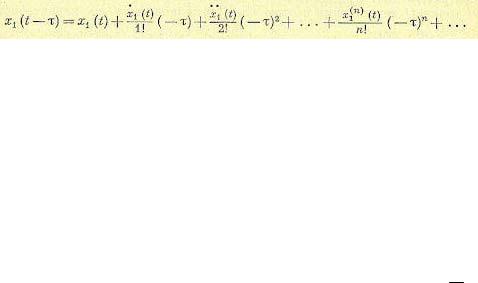
дифференциальным уравнением второго порядка (14.5). Для решения вопроса о том, какое из этих уравнений лучше подходит к данному реальному звену, можно сравнить еще их амплитудно-фазовые характеристики с экспериментально снятой амплитудно-фазовой характеристикой звена, выражающей его динамические свойства при вынужденных колебаниях. Построение амплитудно-фазовых характеристик звеньев с запаздыванием будет рассмотрено ниже.

В целях единства записи уравнений представим второе из соотношений (14.4) дляэлемента запаздывания в операторном виде. Разложив правую часть его в ряд Тейлора, получим

или, в принятой ранее символической операторной записи,

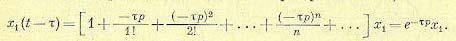(14.6)

Это выражение совпадает с формулой теоремы запаздывания для изображений функций (табл. 7.2). Таким образом, для звена чистого запаздывания получаем передаточную функцию в виде

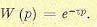(14.7)

Заметим, что в некоторых случаях наличие большого числа малых постоянных времени в системе регулирования можно учесть в виде постоянного запаздывания, равного сумме этих постоянных времени. Действительно, пусть система cодержит N последовательно включенных апериодических звеньев первого порядка с коэффициентом передачи,

равным единице, и величиной каждой постоянной времени ∆T = Nτ . Тогда результирующая пере даточная функция будет

(14.8)

Если N → ∞ , то в пределе получаем W ( p) = e− pτ . Уже при N = 8 …10 передаточная

функция (14.8) мало отличается от передаточной функции звена с запаздыванием (14.6). Уравнение любого линейного звена с запаздыванием (14.4) будем теперь записывать в виде

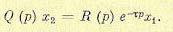(14.9)

Передаточная функция линейного звена с запаздыванием будет

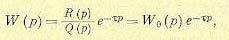(14.10)

где через W0(р) обозначена передаточная функция соответствующего обыкновенного линейного звена без запаздывания.

Частотная передаточная функция получается из (14.10) подстановкой р = jw:

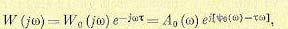(14.11)

где А0 (w) и ψ0 (w) — модуль и фаза частотной передаточной функции звена без

запаздывания. Отсюда получаем следующее правило.

Для построения амплитудно-фазовой характеристики любого линейного звена с запаздыванием нужно взять характеристику соответствующего обыкновенного линейного звена и каждую ее точку сдвинуть вдоль окружности по часовой стрелке на угол τw , где w— значение частоты колебаний в данной точке характеристики (рис. 14.4, а).

Так как в начале амплитудно-фазовой характеристики w = 0, а в конце w= ∞, то начальная точка остается без изменения, а конец характеристики асимптотически навивается на

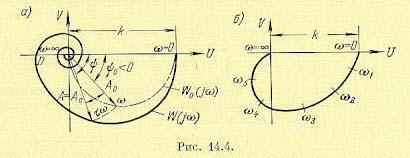
начало координат (если степень операторного многочлена К меньше, чем многочлена Q). Выше говорилось о том, что реальные переходные процессы (временные характеристики) вида рис. 14.3, б часто могут быть с одинаковой степенью приближения описаны как уравнением (14.2), так и (14.5). Амплитудно-фазовые характеристики для уравнений (14.2) и (14.5) показаны на рис. 14.4, а и б соответственно. Принципиальное отличие первой состоит в том, что она имеет точку. В пересечения с осью U. При сравнении обеих характеристик между собой и с экспериментальной амплитудно-фазовой характеристикой реального звена надо принимать во внимание не только форму кривой, но и характер распределения отметок частот со вдоль нее.

Линейная система с запаздыванием. Пусть одноконтурная или многоконтурная автоматическая система в числе своих звеньев имеет одно звено с запаздыванием. Тогда уравнение этого звена имеет вид (14.9). Если таких звеньев несколько, то они могут иметь разные величины запаздывания (τ1 ,τ2 , . . .). Все выведенные в главе 5 общие формулы для

уравнений и передаточных функций систем автоматического регулирования остаются в силе и для любых линейных систем с запаздыванием, если только в эти формулы подставлять значения передаточных функций в виде (14.10).

Например, для разомкнутой цепи из последовательно соединенных звеньев, среди которых имеется два звена с запаздыванием τ1 и τ2 соответственно, передаточная функция разомкнутой системы будет иметь вид

(14.12)

где Wо(р) — передаточная функция разомкнутой цепи без учета запаздывания, равная произведению передаточных функций включенных последовательно звеньев.

Таким образом, при исследовании динамики разомкнутой цепи из последовательно соединенных звеньев безразлично, будет ли все запаздывание сосредоточено в одном каком-нибудь звене или разнесено по разным звеньям. Для многоконтурных цепей получатся более сложные соотношения.

Если имеется звено с отрицательной обратной связью, обладающей запаздыванием т, то оно будет описываться уравнениями:

(14.13)

Передаточные функции звена и цепи обратной связи будут при этом

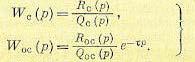(14.14)

Согласно (5.59) результирующая передаточная функция звена вместе с обратной связью будет

(14.15)

Этой передаточной функции соответствует дифференциальное уравнение звена в операторной форме

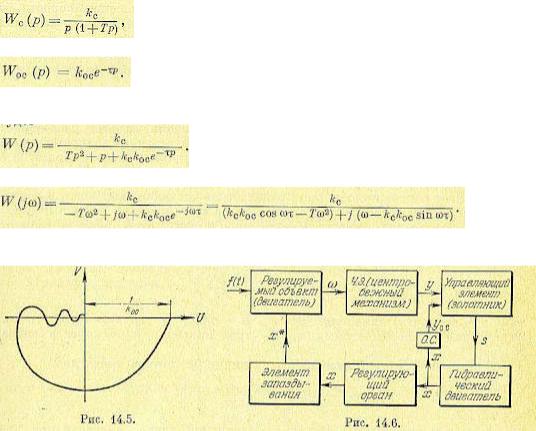
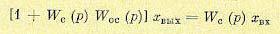(14.16)

или, при подстановке (14.14),

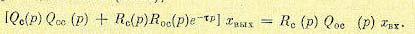(14.17)

Пусть, например, интегрирующее звено с замедлением, передаточная функция которого

охватывается отрицательной обратной связью с передаточной функцией

Тогда результирующая передаточная функция звена с обратной связью в соответствии с

(14.15) будет

Частотная передаточная функция получается подстановкой в последнее выражение р=jw:

Амплитудно-фазовая характеристика, соответствующая этому выражению, приведена для иллюстрации на рис. 14.5.

Пример системы с запаздыванием. Рассмотрим систему регулирования скорости двигателя (рис. 1.16). Составим уравнения всех звеньев системы с учетом их инерционностей. Дополнительно к тому учтем еще запаздывание τ в воздействии регулирующего органа на объект. Изобразим это введением в структурную схему данной системы дополнительного элемента запаздывания (рис. 14.6). Пусть объект не имеет самовыравнивания и снабжен регулятором с жесткой обратной связью (рис. 10.11). Уравнения такой системы

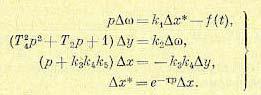(14.18)

Уравнение замкнутой системы

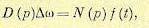(14.19)

где

(14.20)

Здесь ∆w , ∆y , ∆x , ∆x *—приращения скорости, перемещений золотника и

регулирующего органа и управляющего воздействия; k1, . . ., k5—коэффициенты, T2 и T4— постоянные времени.

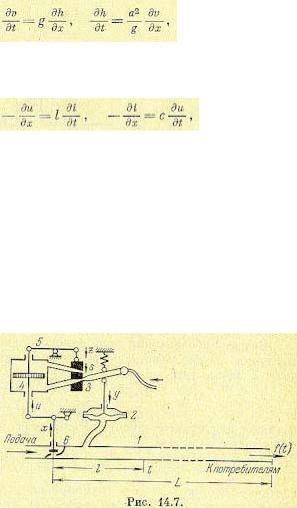
Учтем также условие постоянства массы

(14.22)

и адиабатическое уравнение состояния газа

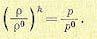(14-23)

В этих уравнениях w, р, р — соответственно скорость, давление и плотность газа в текущем сечении трубопровода с координатой l в момент времени t (вся длина трубопровода обозначается через L); k — показатель степени в уравнении адиабатического состояния газа; индексы 0 вверху (р°, р°) означают, что данные величины относятся к установившемуся состоянию системы. Продифференцировав (14.23), получаем

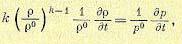(14.24)

Откуда

где а — скорость звука в газе, определяемая формулой

(12.25)

Обычно не учитывают сопротивления движения газа в трубопроводе, пренебрегая сравнительно малыми членами w ∂∂wl и w ∂∂ρl . Кроме того, ввиду малости величины отклонения давления р в процессе регулирования от его установившегося значения можно считать, что pp0 ≈1, а следовательно, согласно (14.23) ρρ0 ≈1. В результате из уравнений

(14.21), (14.22) и (14.24) получаем

(14.26)

Введем обозначения для относительного отклонения <р регулируемой величины от ее установившегося значения и для относительной координаты К вдоль трубопровода:

(14.27)

а также для относительного отклонения λ скорости движения газа в трубопроводе:

(14.28)

где w0 — скорость газа в трубопроводе при установившемся процессе, k— показатель

степени в адиабатическом уравнении состояния газа (14.23). Переходя в уравнениях (14.26) к этим относительным безразмерным переменным и бесконечно малым приращениям, получаем искомые уравнения регулируемого объекта (трубопровода) в виде

(14.29)

где введены два постоянных параметра регулируемого объекта:

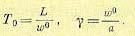(14-30)

Первый из них (Т0) представляет собой, очевидно, время прохождения газа по данному трубопроводу в установившемся процессе, а второй (γ ) — отношение установившейся

скорости газа к скорости звука в нем.

Заметим, что уравнения (14.29) эквивалентны так называемому волновому уравнению

(14.31)

которое легко получается, если первое из уравнений (14.29) продифференцировать по λ , а второе — по t и сравнить результаты дифференцирования.

Для системы уравнений в частных производных (14.29) надо написать граничные условия. Для этого запишем уравнение поступления газа через регулирующий клапан в начале трубопровода и уравнение потребления газа в конце его.

Используем выражение для скорости газа через его расход, а именно:

(14.32)

где G — расход газа по весу в секунду, F — площадь сечения трубопровода, g — ускорение силы тяжести.

Условимся значения всех переменных, относящихся к началу и к концу трубопровода, обозначать индексами 1 и 2 соответственно. Расход газа в начале трубопровода G будем считать функцией координаты перемещения регулирующего клапана х, т. е.

(14.33)

Эта функция (рис. 14.8) определяется либо аналитическим расчетом, либо из опытных данных.

На основании уравнений (14.32), (14.33), а также формул главы 3 малое отклонение ∆w1 величины скорости в начале трубопровода от ее установившегося значения w° будет

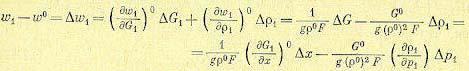(14.34)

установившиеся значения w°, G°, р° пишутся без индекса 1, так как они одинаковы вдоль

всего трубопровода). Величина ∂∂ρx1 есть тангенс угла наклона касательной в точке С

(рис. 14.8), соответствующей установившемуся процессу в трубопроводе. На основании

(14.23) и (14.25)

Введем безразмерную величину относительного отклонения регулирующего клапана:

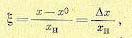(14.35)

где хн — условное номинальное значение, равное

(14.36)

Кроме того, заметим, что согласно (14.32)

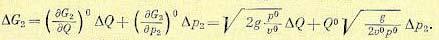
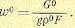(14.37)

Подставляя все это в (14.34), с учетом (14.28) и (14.27) получаем уравнение поступления газа через регулирующий клапан в начале трубопровода;

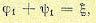(14.38)

которое является первым граничным условием для уравнений объекта (14.29). Расход газа в конце трубопровода у потребителей можно записать согласно (14.32) в виде

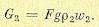(14.39)

С другой стороны, известно, что при выходе газа из трубопровода (в случае критического истечения, которым мы для простоты и ограничимся) будет

(14.40)

где Q — площадь некоторого эквивалентного выходного сечения на конце трубопровода у потребителей (это величина, которая может меняться как угодно по произволу потребителя; она выражает собой, следовательно, внешнее возмущающее воздействие на данную систему регулирования), р2 — давление в конце трубопровода перед выходом к потребителям, υ2 — удельный объем газа там же.

Уравнение для отклонения величины расхода в процессе регулирования от его установившегося значения в линеаризованном виде на основании (14.39), (14.23), (14.37) и (14.27) будет

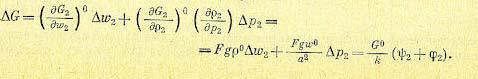(14.41)

Выразим ∆G2 также из (14.40), т. е. через изменение выходного сечения у потребителей, считая для простоты υ2 = const =υ0 :

Учитывая, что из (14.40)

(14.42)

и вводя безразмерную величину изменения выходного сечения, т. е. внешнего возмущающего воздействия

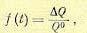(14.43)

получим

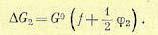(14.44)

Сравнение выражений (14.41) и (14.44) дает искомое уравнение потребления газа в конце трубопровода:

(14.45)

которое является вторым граничным условием для уравнения объекта (14.29). Уравнение потребления (14.45) записано для общего случая процесса регулирования с переменным внешним возмущающим воздействием, выраженным через относительную величину выходного сечения f у потребителей. При исследовании же переходного процесса в системе, когда после некоторого возмущения потребление установилось (Q = соnst f =0), уравнение (14.45) будет иметь вид

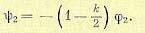(14-46)

Уравнения регулятора. Уравнение чувствительного элемента

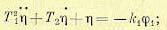(14-47)

здесь T1,Т2 и k1 — постоянные времени и коэффициент передачи, а

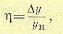(14-48)

Ун — некоторое номинальное перемещение.

Индекс 1 при переменной ϕ в уравнении (14.47) означает, что чувствительный элемент

измеряет давление газа в начале трубопровода. Уравнение управляющего элемента со струйной трубкой

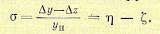(14.49)

Уравнение пневматического двигателя на основании (5.137) будет

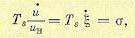(14.50)

где Тs — время двигателя.

Уравнение жесткой обратной связи согласно рис. 14.7 будет

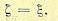(14.51)

Уравнение всей системы регулирования. Итак, для данной системы автоматического регулирования имеем уравнения объекта (14.29) с граничными условиями (14.38) и (14.45)

или (14.46) и уравнения регулятора (14.47), (14.49), (14.50) и (14.51).

Решение уравнений в частных производных (14.29), как известно, можно записать в виде следующей суммы некоторых двух функций от аргументов ( t −γT0 λ ) и ( t + γT0 λ ):

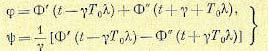(14.52)

(легко проверить, что при подстановке этих выражений уравнения (14.29) удовлетворяются тождественно).

Для определения функций Ф' и Ф" используются граничные условия. При исследовании переходного процесса уравнение потребления газа в конце трубопровода (т. е. второе граничное условие) возьмем в виде (14.46). Это соответствует значению l = L, т. е. λ = 1. Поэтому из условия (14.46) с подстановкой (14.52) получаем

откуда

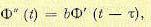(14.53)

где обозначено

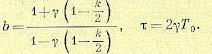(14.54)

Для начала трубопровода, где λ = 0, из (14.52) с учетом (14.53) получаем:

(14.55)

К этим уравнениям надо присоединить первое граничное условие (14.38) и уравнения регулятора.

Запишем теперь все уравнения системы регулирования в символической операторной форме, заметив предварительно, что согласно § 14.1 равенство (14.53) в операторной форме имеет вид