
Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975
.pdf
будет иметь вид бесконечной лестницы (рис. 11.6), но не заходящей выше единицы, т.е.
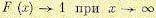 .
.
Вероятностные характеристики непрерывных случайных величин. Непрерывная случайная величина может принимать все значения в каком-либо заданном ограниченном интервале
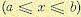 или все значения от —∞ до +∞. Следовательно, функция распределения (интегральный закон распределения) для непрерывной случайной величины будет изображаться непрерывной кривой. На рис. 11.7 показаны оба упомянутых выше варианта.
или все значения от —∞ до +∞. Следовательно, функция распределения (интегральный закон распределения) для непрерывной случайной величины будет изображаться непрерывной кривой. На рис. 11.7 показаны оба упомянутых выше варианта.
Вероятность того, что непрерывная случайная величина примет определенное числовое значение х, бесконечно мала (например, вероятность попадания центра тяжести снаряда в определенную точку цели). Вероятность же того, что непрерывная случайная величина
окажется в некотором промежутке 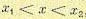 , будет иметь конечное значение, а именно:
, будет иметь конечное значение, а именно:
Вероятность того, что непрерывная случайная величина содержится в промежутке между х и х + dх, будет
Величина
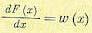 (11.11)
(11.11)
называется плотностью вероятности.
Закон распределения для непрерывной случайной величины в отличие от дискретной задается не в виде значений вероятности, а в виде плотности-вероятности ω (х), называемой также дифференциальным законом распределения. На рис. 11.8 показаны дифференциальные законы распределения для двух вариантов функции распределения F (х), показанных на рис. 11.7. Если .бы здесь использовалось то же понятие закона распределения, что и для дискретной случайной величины, то получились бы бесконечно малые ординаты P (х).
Выражение ω (х) их означает вероятность того, что случайная величина содержится между х и х + Ах:

Вероятность того, что случайная величина содержится между значениями х1 и х2, определяется формулой
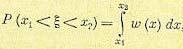 (11.12)
(11.12)
что геометрически выражается заштрихованной площадью на рис. 11.8. Кроме того, имеет место зависимость
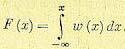 (11.13)
(11.13)
Вся площадь под кривой ω (х) равна единице:
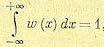 (11.14)
(11.14)
так как 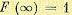 .
.
Формула (11.14) соответствует моменту нулевого порядка. Среднее значение (метематическое ожидание) соответствует моменту первого порядка:
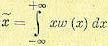 (11.15)
(11.15)
что вытекает из формулы (11.5) как предел суммы. Моменты высших порядков по аналогии с (11.6) будут
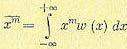 (11.16)
(11.16)
Таким же образом можно вычислить центральный момент m-го порядка
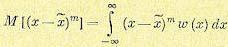 (11.17)
(11.17)
Как и в случае дискретных случайных величин, центральный момент первого порядка всегда равен нулю.
Рассеяние непрерывной случайной величины можно оценивать одним из следующих значений, словесные формулировки которых остаются прежними.
Среднее отклонение (мало удобная для вычислений величина)
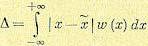 (11.18)
(11.18)
Дисперсия (наиболее удобная для вычислений величина)
(11.19)
Среднеквадратичное отклонение
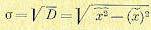 (11.20)
(11.20)
Средневероятным отклонением Ав называется такая величина, при которой отклонения 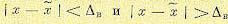 имеют одинаковую вероятность.
имеют одинаковую вероятность.
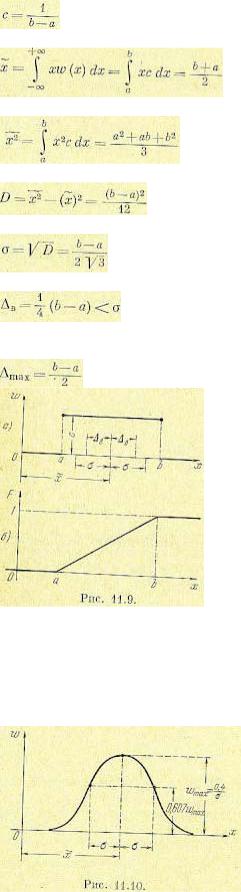
Рассмотрим простейшие типовые законы распределения непрерывных случайных величин. 1. Равномерное распределение случайной величины на определенном участке характеризуется плотностью вероятности ω (х) и функцией распределения F (х), показанными на рис. 11.9. При этом на основании свойства (11.14) имеем
Подсчитаем характерные значения. Среднее значение (математическое ожидание)
Среднее значение квадрата случайной величины (момент второго порядка)
Дисперсия
Среднеквадратичное отклонение
Средневероятное отклонение
Максимально возможное отклонение случайной величины от среднего значения в данном случае будет
2. Нормальный закон распределения непрерывных случайных величин (закон Гаусса). Этот закон имеет вид
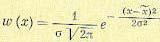 (11.21)
(11.21)
где σ — среднеквадратичное отклонение, а 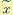 — математическое ожидание случайной величины.
— математическое ожидание случайной величины.
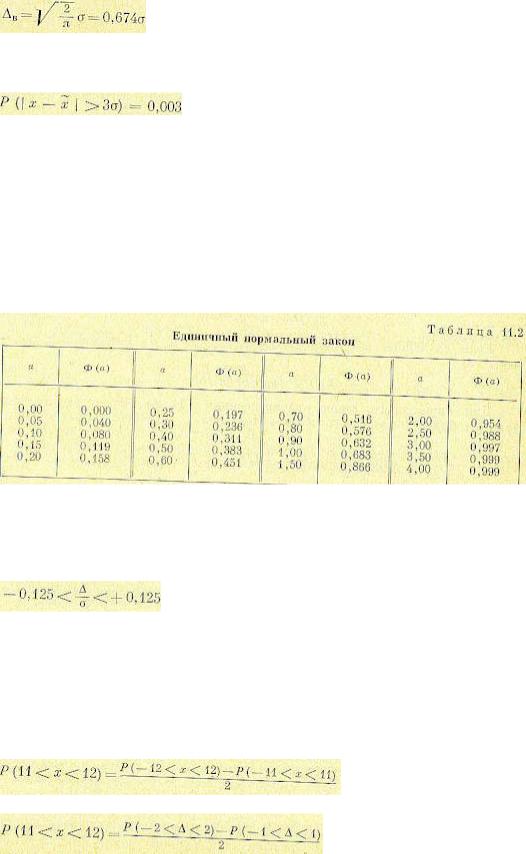
График для этого закона изображен на рис. 11.10. Он имеет типичную «колоколообразную» форму.
Анализ условий возникновения нормального распределения показывает, что оно имеет место во всех тех случаях, когда случайная величина характеризует собой
суммарный эффект большого числа независимых причин. Поэтому нормальное распределение весьма часто встречается на практике.
Для этого закона средневероятное отклонение будет
За максимальное отклонение, которое может иметь место, обычно принимают величину
 , так как вероятность того, что отклонение
, так как вероятность того, что отклонение  будет больше 3σ, очень мала, а именно:
будет больше 3σ, очень мала, а именно:
Для удобства расчетов составлены таблицы для единичного нормального закона. Для
получения этого закона положим  и введем новую относительную переменную
и введем новую относительную переменную  . Тогда вероятность того, что текущее значение
. Тогда вероятность того, что текущее значение
относительной переменной находится в интервале от —а до +а или сама переменная находится в интервале от 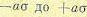 , определится выражением
, определится выражением
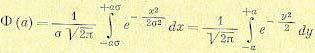 (11.22)
(11.22)
Для функции Ф (а) составлены подробные таблицы. В качестве иллюстрации приводится краткая табл. 11.2.
Рассмотрим пример пользования таблицей. Пусть имеется некоторая случайная величина ж,
для которой математическое ожидание  , а среднеквадратичное отклонение составляет
, а среднеквадратичное отклонение составляет
 . Определим, какова вероятность того, что случайная величина лежит в интервале 9,5 < х < 10,5. Это означает, что отклонение от математического ожидания должно лежать в интервале — 0,5 < ∆ < +0,5. Для. относительных величин это соответствует неравенству
. Определим, какова вероятность того, что случайная величина лежит в интервале 9,5 < х < 10,5. Это означает, что отклонение от математического ожидания должно лежать в интервале — 0,5 < ∆ < +0,5. Для. относительных величин это соответствует неравенству
Таким образом, а = 0,125. По табл. 11.2 определяем путем интерполяции вероятность Ф(а)=0,1.
Произведем более сложный расчет. Пусть для той же случайной величины необходимо определить вероятность нахождения ее в интервале 11 < х < 12. Так как кривая нормального распределения является симметричной относительно среднего значения случайной величины, то искомая вероятность может быть найдена как половина разности вероятности нахождения случайной величины в интервале — 12 < х < 12 и вероятности нахождения в интервале — 11 << х < 11, т. е.
или для отклонений
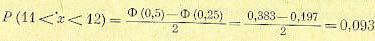
Перейдя к относительным величинам, получаем в результате искомую вероятность
Характеристические функции. Введем в рассмотрение функцию 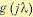 , связанную с плотностью вероятности ω (х) взаимным преобразованием Фурье:
, связанную с плотностью вероятности ω (х) взаимным преобразованием Фурье:
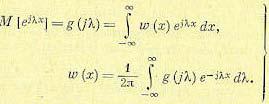 (11.23)
(11.23)
Эта функция называется характеристической. Ее основные свойства следующие. Если случайная величина у = ах+b, то
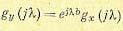 (11.24)
(11.24)
Если случайная величина 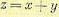 , где х и у — независимые величины, то
, где х и у — независимые величины, то
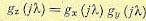 (11.25)
(11.25)
Для нормального закона распределения (11.21) характеристическая функция будет
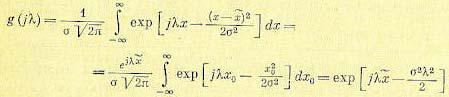 (1.1 .26)
(1.1 .26)
По характеристической функции могут быть найдены моменты случайной величины. Разлагая 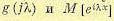 в первой формуле (11.23) в ряд: Маклорена, имеем
в первой формуле (11.23) в ряд: Маклорена, имеем
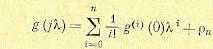 (11.27)
(11.27)
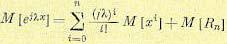 (11.28)
(11.28)
Из сравнения (11.27) и (11.28) можно получить формулу для момента m-го порядка:
 (11.29)
(11.29)
Аналогичным образом можно получить формулу для центрального-момента m-го порядка:
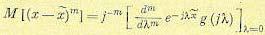 (11.30)
(11.30)
Формулы (11.29) и (11.30) могут быть использованы для вычисления моментов. Векторные случайные величины. Пусть имеется совокупность случайных величин 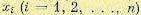 . Такая совокупность может быть представлена в виде матрицы-столбца.
. Такая совокупность может быть представлена в виде матрицы-столбца.
Если физические размернрсти всех величин одинаковы, то матрица-столбец может быть отождествлена с вектором. При разных размерностях переход к вектору может быть сделан после нормирования (введения весовых коэффициентов).
Пусть, например, имеются две непрерывные случайные величины x1 и x2. Для них может быть введена двумерная плотность вероятности 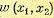 . Если величины х1 и х2 независимы, то
. Если величины х1 и х2 независимы, то
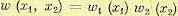 .
.
Вводится понятие смешанного момента m-го порядка, где 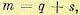
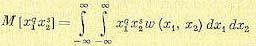 (11.31)
(11.31)
и смешанного центрального момента
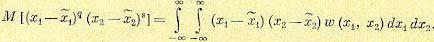 (11.32)
(11.32)
Если q = s = 1, то центральный момент второго порядка имеет особое значение и носит название корреляционного момента:
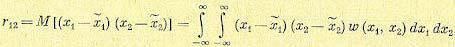 (11.33)
(11.33)
В случае независимости случайных величин х1 и х2 можно легко показать, что корреляционный момент r12 = 0.
Иногда употребляется понятие коэффициента корреляции, представляющего собой относительное значение корреляционного момента:
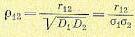 (11.34)
(11.34)
где D1 и D2 — дисперсии величин х1 и х2.
Для совокупности случайных величин 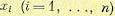 в приближенных расчетах часто
в приближенных расчетах часто
ограничиваются заданием матрицы-столбца (вектора) математических ожиданий 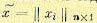 и матрицы корреляционных моментов
и матрицы корреляционных моментов
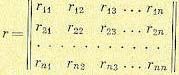 (11.35)
(11.35)
Составляющие корреляционной матрицы показывают степень связи между отдельными случайными величинами, причем  . На диагонали корреляционной матрицы находятся собственные центральные моменты второго порядка, т. е. дисперсии
. На диагонали корреляционной матрицы находятся собственные центральные моменты второго порядка, т. е. дисперсии  .
.
§ 11.2. Случайные процессы
Случайная величина х, изменяющаяся во времени t, называется случайным или стохастическим процессом. Случайный процесс не есть определенная кривая х (t), а является множеством возможных кривых х (t), так же как случайная величина не имеет определенного значения, а является совокупностью (множеством) возможных значений.
Можно еще сказать, что случайный процесс есть такая функция времени, значение которой в каждый момент времени является случайной величиной.
Примерами случайных процессов могут, например, являться: координаты самолета, замеряемые радиолокационной станцией; угол визирования движущейся цели головкой самонаведения; помехи в системе телеуправления; нагрузка электрической сети и т. п.
Итак, в случайном процессе нет определенной зависимости х (t). Каждая кривая множества (рис. 11.11) является лишь отдельной реализацией случайного процесса. Никогда нельзя сказать заранее, по какой кривой пойдет процесс.
Однако случайный процесс может быть оценен некоторыми вероятностными характеристиками.
В каждый отдельный момент времени наблюдаются случайные величины
наблюдаются случайные величины 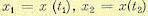 , каждая из которых имеет
, каждая из которых имеет
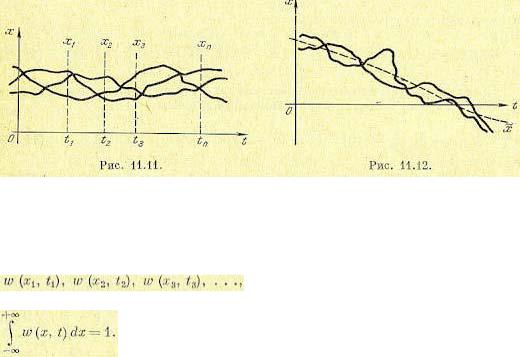
свой закон распределения. Поскольку это — непрерывная случайная чина, то надо пользоваться понятием плотности вероятности.
Обозначим 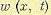 закон распределения для всех этих отдельных случайных величин. В общем случае он меняется с течением времени. Для каждого данного t в отдельности
закон распределения для всех этих отдельных случайных величин. В общем случае он меняется с течением времени. Для каждого данного t в отдельности
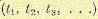 будет свой закон распределения:
будет свой закон распределения:
причем по свойству (11.14) для каждого из них
Для каждого заданного момента времени можно найти характеристики случайных величин, определенные в § 11.1. В результате будем иметь среднее по множеству (математическое ожидание)
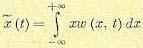 (11.36)
(11.36)
и дисперсию
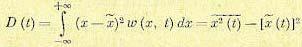 (11,37)
(11,37)
Среднее значение случайного процесса представляет собой некоторую среднюю кривую (рис. 11.12), около которой группируются все возможные отдельные реализации этого процесса, а дисперсия D(t) или среднеквадратичное отклонение σ(t) характеризуют рассеяние отдельных возможных реализаций процесса около этой средней кривой.
Кроме этих осредненных характеристик 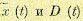 , которые для каждого данного момента времени являются средними по множеству, введем понятие среднего значения случайной
, которые для каждого данного момента времени являются средними по множеству, введем понятие среднего значения случайной
величины  для отдельной реализации случайного процесса х (t), которое определяется из выражения
для отдельной реализации случайного процесса х (t), которое определяется из выражения
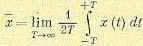 (11.38)
(11.38)
Переход к пределу здесь необходим для того, чтобы характеризовать не какой-нибудь отдельный участок кривой, а всю возможную кривую х (t) в целом.
Для того чтобы знать связь между возможными значениями случайной функции х (г) ъ последующие моменты времени со значениями в предыдущие моменты, вводится понятие двумерной плотности вероятности
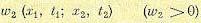 ,
,
смысл которого можно пояснить следующим образом. Вероятность того, что в момент времени t1 величина х находится в интервале 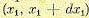 , а в момент времени t2 — в интервале
, а в момент времени t2 — в интервале 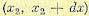 , будет
, будет 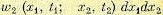 . Это есть вероятность того, что кривая х (t) пройдет вблизи двух заданных точек
. Это есть вероятность того, что кривая х (t) пройдет вблизи двух заданных точек 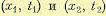 . Вводится также и тг-мерная плотность вероятности
. Вводится также и тг-мерная плотность вероятности
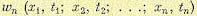 .
.

Если ее умножить на |
, то это будет вероятность того, что кривая пройдет |
|
вблизи заданных п точек. |
|
|
Случайный процесс полностью определяется видом функций |
и связью |
|
между ними.
Простейшим типом случайного процесса является чисто случайный процесс. В таком процессе все значения случайной величины в отдельные моменты времени 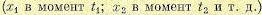 не зависят друг от друга. Тогда появления значений
не зависят друг от друга. Тогда появления значений 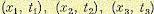 и т.д. будут независимыми случайными событиями, для которых вероятность их совместного наступления равна, как известно, произведению вероятностей наступления каждого из них в отдельности. Следовательно, для чисто случайного процесса
и т.д. будут независимыми случайными событиями, для которых вероятность их совместного наступления равна, как известно, произведению вероятностей наступления каждого из них в отдельности. Следовательно, для чисто случайного процесса
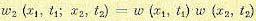 (11.39)
(11.39)
и вообще
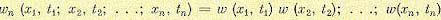 (11.40)
(11.40)
Это — самые простые соотношения в теории случайных процессов. Они могут применяться для характеристики некоторых видов помех (чисто случайные хаотические помехи).
Для характеристики полезных входных сигналов систем регулирования и следящих систем соотношения (11.39) и (11.40) практически не могут применяться, так как для этих сигналов ход процесса в последующие моменты времени в какой-то степени зависит от того, что было в предыдущие моменты времени.
Так, например, если речь идет о слежении за самолетом, то он не может как угодно быстро менять свое положение и скорость. Поэтому если он в момент времени t1 занял положение х1, то этим самым его возможное положение х2 в следующий момент t2 ограничено, т. е. события 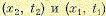 не будут независимыми. Чем более инерционен изучаемый объект, тем больше эта взаимозависимость, или корреляция. В таких случаях вместо формулы (11.39) необходимо записать
не будут независимыми. Чем более инерционен изучаемый объект, тем больше эта взаимозависимость, или корреляция. В таких случаях вместо формулы (11.39) необходимо записать
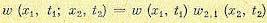 (11.41)
(11.41)
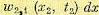 — условная вероятность того, что случайный процесс пройдет вблизи точки
— условная вероятность того, что случайный процесс пройдет вблизи точки
 , если он уже прошел через точку
, если он уже прошел через точку 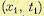 . Следовательно, зная плотности вероятности ю
. Следовательно, зная плотности вероятности ю
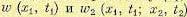 , можно найти также и условную плотность вероятности
, можно найти также и условную плотность вероятности
 (11.42)
(11.42)
Кроме того, имеет место следующая связь между основными плотностями вероятности:
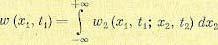 (11 43)
(11 43)
так как 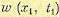 есть плотность вероятности случайной величины
есть плотность вероятности случайной величины 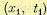 безотносительно к тому, какое потом будет значение
безотносительно к тому, какое потом будет значение 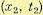 , т. е. допускается
, т. е. допускается 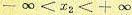 . Аналогичным образом любая плотность вероятности низшего порядка всегда может быть получена из высшей, т. е. высшие плотности вероятностей содержат наибольшее количество информации о случайном процессе (о взаимосвязях между возможными значениями случайной величины х в различные моменты времени).
. Аналогичным образом любая плотность вероятности низшего порядка всегда может быть получена из высшей, т. е. высшие плотности вероятностей содержат наибольшее количество информации о случайном процессе (о взаимосвязях между возможными значениями случайной величины х в различные моменты времени).
Написанные соотношения справедливы для случайных процессов любых типов. В зависимости же от того, до какого порядка принимаются во внимание плотности вероятности, а
также от разных дополнительных гипотез о формах связи между  рассматриваются разные типы случайных процессов в отличие от чисто случайных.
рассматриваются разные типы случайных процессов в отличие от чисто случайных.
Другая классификация всех случайных процессов состоит в разделении их на стационарные и нестационарные. Теория стационарных случайных процессов наиболее разработана и чаще всего применяется на практике.
§ 11.3. Стационарные случайные процессы
Стационарным случайным процессом называется такой процесс, вероятностные характеристики которого не зависят от времени. Все плотности вероятностей  не меняются при любом сдвиге рассматриваемого участка процесса во времени, т. е. при сохранении постоянной разности.
не меняются при любом сдвиге рассматриваемого участка процесса во времени, т. е. при сохранении постоянной разности.
Можно сказать, что стационарный случайный процесс в какой-то мере аналогичен обычным стационарным или установившимся процессам в автоматических системах. Например, при рассмотрении обычных установившихся периодических колебаний ничего не изменится, если перенести начало отсчета на какую-нибудь величину. При этом сохранят свои значения такие характеристики, как частота, амплитуда, среднеквадратичное значение и т. п. В стационарном случайном процессе закон распределения один и тот же для каждого момента времени, т. е. плотность вероятности не зависит от времени:  .
.
Отсюда получаем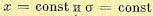 вдоль всего случайного процесса. Следовательно, в стационарном случайном процессе средняя линия, в отличие от общего случая (см. рис. 11.12),
вдоль всего случайного процесса. Следовательно, в стационарном случайном процессе средняя линия, в отличие от общего случая (см. рис. 11.12),
будет прямая 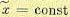 , подобно постоянному смещению средней линии обычных периодических колебаний. Рассеяние значений переменной х в стационарном случайном
, подобно постоянному смещению средней линии обычных периодических колебаний. Рассеяние значений переменной х в стационарном случайном
.процессе, определяемое 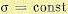 , также будет все время одинаковым, подобно постоянному значению среднеквадратичного отклонения обычных установившихся колебаний от средней линии.
, также будет все время одинаковым, подобно постоянному значению среднеквадратичного отклонения обычных установившихся колебаний от средней линии.
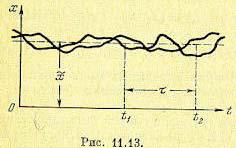
Аналогичным образом и двумерная плотность вероятности также будет «одна и та же для одного и того же промежутка времени 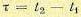 между любыми t1 и t2 (рис. 11.13), т. е.
между любыми t1 и t2 (рис. 11.13), т. е.
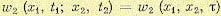 (11.44)
(11.44)
и также для n-мерной плотности вероятности.
Задание всех этих функций распределения плотности определяет случайный процесс. Однако более удобно иметь дело с некоторыми осреднен-ными и характеристиками процесса.
Прежде чем перейти к ним, отметим два важных для практики ^свойства.
1.Ограничиваясь только стационарными случайными процессами, можно будет определить только установившиеся (стационарные) динамиче--ские ошибки автоматических систем при случайных воздействиях. Такой прием применялся и ранее при рассмотрении регулярных воздействий, когда определялись динамические свойства систем регулирования по величине динамических ошибок в установившемся периодическом режиме.
2.Стационарные случайные процессы обладают замечательным свойством, которое известно под названием эргодической гипотезы.
Для стационарного случайного процесса с вероятностью, равной единице (т. е. практически достоверно), всякое среднее по множеству равно соответствующему среднему по времени, в
частности 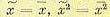 и т. д.
и т. д.
В самом деле, поскольку вероятностные характеристики стационарного случайного
процесса с течением времени не меняются (например, 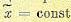 ), то длительное наблюдение случайного процесса на одном объекте (среднее ло времени) дает в среднем такую же картину, как и большое число наблюдений, сделанное в один и тот же момент времени на большом числе одинаковых объектов (среднее по множеству).
), то длительное наблюдение случайного процесса на одном объекте (среднее ло времени) дает в среднем такую же картину, как и большое число наблюдений, сделанное в один и тот же момент времени на большом числе одинаковых объектов (среднее по множеству).
Для многих случаев существует математическое доказательство этого свойства. Тогда оно сводится к эргодической теореме.

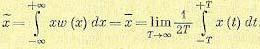 (11.45)
(11.45)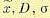 и т. п., вместо параллельного испытания многих однотипных систем в один и тот же момент времени, пользоваться одной кривой х (t), полученной при испытании одной системы в течение длительного времени.
и т. п., вместо параллельного испытания многих однотипных систем в один и тот же момент времени, пользоваться одной кривой х (t), полученной при испытании одной системы в течение длительного времени.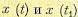 , взятых в моменты времени t и t1 носит название корреляционной (автокорреляционной) функции. Она может быть найдена аналогично (11.31) из выражения
, взятых в моменты времени t и t1 носит название корреляционной (автокорреляционной) функции. Она может быть найдена аналогично (11.31) из выражения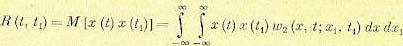 (11.46)
(11.46)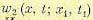 — двумерная плотность вероятности.
— двумерная плотность вероятности.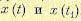 , т. е.
, т. е.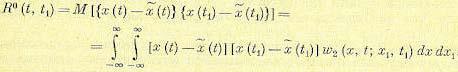 (11.47)
(11.47)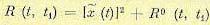 (11.48)
(11.48)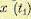 от предшествующего значения х (t) в момент времени t. Это есть мера связи между ними. Рассмотрим основные свойства корреляционных функций.
от предшествующего значения х (t) в момент времени t. Это есть мера связи между ними. Рассмотрим основные свойства корреляционных функций.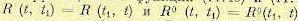 .
. корреляционная функция
корреляционная функция 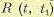 дает средний квадрат случайной величины, а
дает средний квадрат случайной величины, а 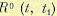 — дисперсию:
— дисперсию: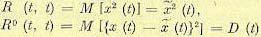 .
.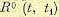 не изменится, если к случайной функции добавить произвольную неслучайную
не изменится, если к случайной функции добавить произвольную неслучайную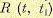 , так кай добавление неслучайных величин к случайным изменяет начальные моменты. В этом случае корреляционная функция будет равна сумме корреляционных функций случайной и неслучайной функций.
, так кай добавление неслучайных величин к случайным изменяет начальные моменты. В этом случае корреляционная функция будет равна сумме корреляционных функций случайной и неслучайной функций.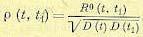 (11.49)
(11.49)