
Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975
.pdf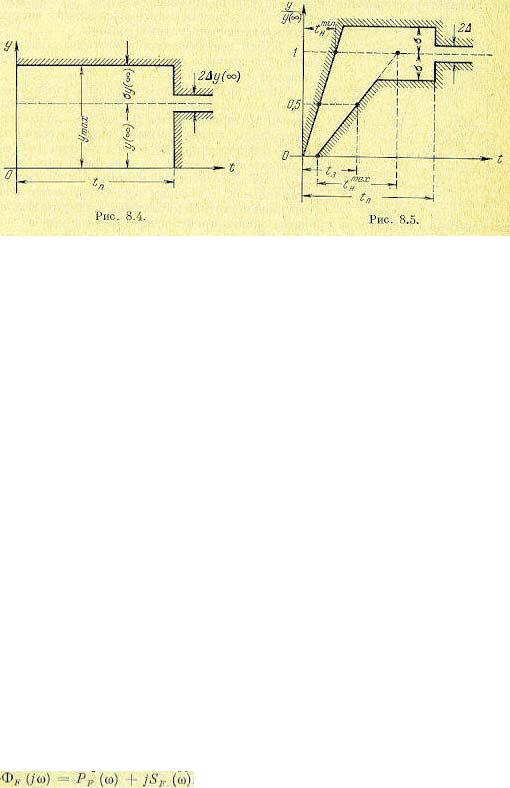
Графически требования к запасу устойчивости и быстродействию сводятся к тому, чтобы отклонение регулируемой величины не выходило при единичном входном воздействии из некоторой области, изображенной На рис. 8.4. Эта область называется областью допустимых отклонений регулируемой величины в переходном процессе.
В следящих системах удобно применять сформулированные требования качества к ошибке системы х (t) = g (t) — у (t). В этом случае можно рассматривать область допустимых значений ошибки и при более сложных входных воздействиях, например при мгновенном приложении на входе постоянной скорости.
Дальнейшее развитие критериев качества, использующих переходную характеристику, приводит к введению дополнительных оценок качества (кроме введенных выше tп, ymax и σ%). К ним относятся следующие оценки.
1.Время запаздывания t3, равное отрезку времени, заключенному между моментом приложения входного скачкообразного сигнала и моментом времени, при котором осредненная выходная величина становится равной половине ее установившегося значения. Примененный здесь термин «осредненная» означает, что в случаях, когда на передний фронт выходного сигнала накладываются высокочастотные колебания (это может иметь место в системах
высокого порядка), величина t3 определяется по сглаженной кривой, аппроксимирующей реальную переходную характеристику системы.
2.Время нарастания tн, равное отрезку времени, заключенному между точкой пересечения оси времени с касательной, проведенной к осредненщщ кривой переходной характеристики в
точке t = t3, и координатой t точки пересечения указанной касательной с горизонтальной прямой, соответствующей установившемуся значению регулируемой величины. Максимальное время
нарастания tmax(н) ограничивается требуемым быстродействием. Минимальное время нарастания tmin(н) ограничивается допустимыми в системе ускорениями и колебательными режимами.
Уточненная диаграмма качества переходного процесса изображена на рис. 8.5.
§ 8.5. Приближённая оценка вида переходного процесса по вещественной частотной характеристике.
Построение кривой переходного процесса является в большинстве случаев весьма трудоемкой операцией. Поэтому целесообразно использовать методы, позволяющие определить вид переходной характеристики без построения всей кривой процесса. Это можно сделать по вещественной частотной характеристике Р (ω) замкнутой системы, которая используется для построения переходной функции (см. § 7.5). При этом предполагается, что лереходный процесс у(t) вызван скачком .задающего воздействия g(t). Возможна оценка вида переходного процесса при приложении скачка возмущения f(t). В этом случае необходимо использовать вещественную часть частотной передаточной функции системы по возмущающему воздействию

Использование оценки вида переходного процесса по вещественной частотной характеристике наиболее удобно применять в том случае, когда для исследования автоматической системы используются частотные методы.
Пусть вещественная частотная характеристика замкнутой системы имеет вид, изображенный на рис. 8.6.
Интервал частот  , в котором
, в котором 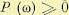 , называется интервалом положительности. Интервал частот
, называется интервалом положительности. Интервал частот 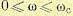 называется интервалом существенных частот, если при ω = ωc и далее при ω > ωc величина |Р (ω) | становится и остается меньше некоторой заданной достаточно малой положительной величины δ. Влиянием остальной части вещественной
называется интервалом существенных частот, если при ω = ωc и далее при ω > ωc величина |Р (ω) | становится и остается меньше некоторой заданной достаточно малой положительной величины δ. Влиянием остальной части вещественной
частотной характеристики (при 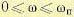 ) на качество переходного процесса можно пренебречь. Если же при ω > ωп оказывается, что |Р(ω)|<0,2Р(ω), то при оценке качества переходного процесса в первом приближении можно принимать во внимание только интервал
) на качество переходного процесса можно пренебречь. Если же при ω > ωп оказывается, что |Р(ω)|<0,2Р(ω), то при оценке качества переходного процесса в первом приближении можно принимать во внимание только интервал
положительности 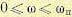 .
.
Заметим, что отбрасываемый «хвост» вещественной частотной характеристики (ω > ωc или ω > ωп) влияет главным образом на начальную часть переходного процесса, которая, следовательно, будет оцениваться более грубо. Начало же вещественной частотной характеристики определяет главным образом концевую часть переходного процесса.
На основании анализа интеграла (7.53) были получены следующие оценки качества переходного процесса.
1.Статическое отклонение у (∞) регулируемой величины, получающееся в результате единичного скачка внешнего воздействия, равно начальному значению вещественной частотной характеристики Р (0). Если речь идет о скачке задающего воздействия, то Р (0) должно равняться
либо 1, либо некоторому k0, если система должна воспроизводить задающее воздействие в определенном масштабе k0. Если же вводится скачок возмущающего воздействия f, то значение РF (0) должно быть как можно меньше, причем в астатической системе возможно РF(0) = 0.
2.Чтобы величина перерегулирования ymax — y (∞) (кривая 1 на рис. 8.7, а) не превышала 18% от статического отклонения, достаточно иметь положительную невозрастающую непрерывную характеристику Р (ω) (кривая 1 на рис. 8.7, б).
3.Для монотонности переходного процесса у (t) (кривая 2 на рис. 8.7, а) достаточно, чтобы dР/dω представляла собой отрицательную, убывающую по модулю непрерывную функцию от со (кривая 2 на рис, 8.7, б), причем P(∞)=0
4.Простейшим признаком немонотонности переходного процесса является наличие значений Р (∞) >Р (0) (кривая 3 на рис. 8.7, б). Переходный процесс тоже будет немонотонным, когда кривая Р (∞)
располагается при каких-нибудь со выше ступенчатой кривой С (∞) (рис. 8.7, в), причем
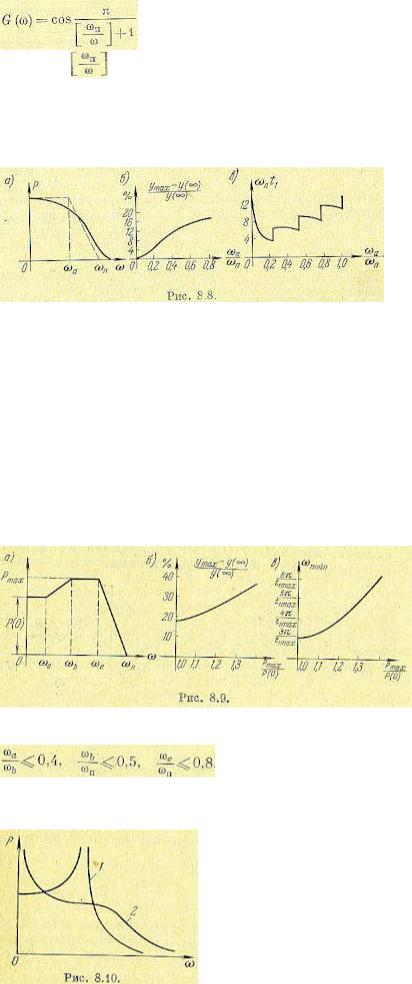
где через |
обозначены целочисленные значения, взятые с избытком; например, |
если  , то берется
, то берется  .
.
5. В случае, если вещественная частотная характеристика Р (∞) имеет очертание вида кривой 3 (рис. 8.7, б), которую можно представить как разность двух положительных невозрастающих непрерывных функций,
то величина перерегулирования ymax — y(∞) (рис. 8.7, а) будет меньше, чем 1,18 Рmax-Р (0). 6. Для монотонных процессов y (t) время затухания t1 до значения
y = 5% от статического отклонения y (∞) будет больше, чем  . В общем же
. В общем же
случае . Вообще при прочих равных условиях переходный процесс тем быстрее затухает, чем больше ∞п, т. е. чем больше растянута область положительности вещественной; частотной характеристики Р (ω) вдоль оси ω.
. Вообще при прочих равных условиях переходный процесс тем быстрее затухает, чем больше ∞п, т. е. чем больше растянута область положительности вещественной; частотной характеристики Р (ω) вдоль оси ω.
7. Если заданную вещественную частотную характеристику Р (ω) можно приближенно заменить трапецией (рис. 8.8, а), то в зависимости от отношения длин оснований ωа и ωп трапеции величина перерегулирования в процентах и время затухания переходного процесса в относительном виде ωпt1 могут быть приближённо оценены графиками, показанными на рис. 8.8,
б и 8.8, в, причем величина t1 заключается в интервале — 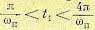
8 . Если заданную характеристику Р(ω) можно приближенно заменить ломаной, изображенной на рис. 8.9, а, причем
то зависимость максимально возможного перерегулирования (в процентах)
от величины отношения 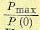 определяется кривой на рис. 8.9, б.
определяется кривой на рис. 8.9, б.
При этом заданной верхней границе допустимого значения времени затухания переходного процесса t1 соответствует нижняя допустимая граница величины интервала положительности ωпmin определяемая кривой на рис. 8.9, в.
9. Склонность системы к колебаниям тем больше, чем выше пик у вещественной характеристики. В частности, этот пик уходит в бесконечность, если система находится на границе колебательной устойчивости, что соответствует наличию пары чисто мнимых корней (кривая 1 на рис. 8.10). При нахождении системы на границе устойчивости, соответствующей наличию одного нулевого корня, в бесконечность уходит начальное значение ординаты Р (0) вещественной частотной характеристики (кривая 2 на рис. 8.10).
На основании вышеуказанных простых признаков можно грубо оценивать качество переходного процесса в замкнутой автоматической системе по виду ее вещественных частотных характеристик Р (ω) и РF (ω).
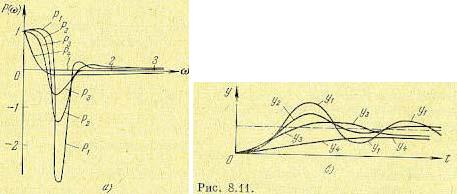
Для иллюстрации, следуя В. В. Солодовникову, приведем ряд кривых переходного процесса у1(t), у2(t), у3(t), у4(t) (рис. 8.11, б), которые соответствуют вещественным частотным
характеристикам замкнутой системы  , изображенным на рис. 8.11, а. Наилучший переходный процесс у3 (t) соответствует характеристике Р3 (ω), а наихудший у1(t)
, изображенным на рис. 8.11, а. Наилучший переходный процесс у3 (t) соответствует характеристике Р3 (ω), а наихудший у1(t)
—характеристике Р4 (ω), обладающей наибольшими пиками.
§8.6. Корневые методы
Как было сказано выше, вид корней характеристического уравнения определяет характер переходных процессов в системе автоматического регулирования. Поэтому можно сформулировать требования по запасу устойчивости и быстродействию системы, не рассматривая самих переходных процессов, а накладывая определенные условия на корни характеристического уравнения.
Пусть характеристическое уравнение системы имеет вид
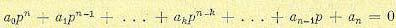 , (8.25)
, (8.25)
где р = с + j ω — комплексное число.
Используя понятие среднегеометрического корня
 (8.26)
(8.26)
где р1, р2, . . ., рn — корни характеристического уравнения, в формуле (8.25) можно перейти к новой комплексной величине q путем подстановки 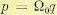 . В результате получим уравнение
. В результате получим уравнение
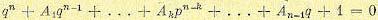 (8.27)
(8.27)
в котором безразмерные коэффициенты 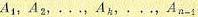 определяются выражением
определяются выражением
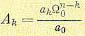 (8.28)
(8.28)
а его корни равны 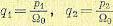 и т. д.
и т. д.
Исходное характеристическое уравнение (8.25) при возвращении к прежней комплексной величине получает вид
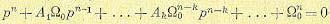 (8.29)
(8.29)
Среднегеометрический корень Ω0 может служить мерой быстроты протекания переходных процессов. Если в уравнении (8.29) увеличить Ω0, например, в 10 раз, то на основании теоремы подобия (табл. 7.2) переходный процесс, оставаясь подобным сам себе, будет протекать в 10 раз быстрее.
В связи с этим можно рассматривать (8.27) как некоторое нормированное характеристическое уравнение, которому соответствует переходный процесс, построенный для безразмерного времени t0 = Ω0t. Если качество переходного процесса является приемлемым с точки зрения допустимого запаса устойчивости, определяемого, например, перерегулированием (рис. 8.3), то требуемая быстрота протекания переходного процесса может быть обеспечена соответствующим выбором величины Ω0.
Для увеличения величины Ω0, как следует из (8.26), необходимо увеличивать свободный член характеристического уравнения аn. Напомним, что в статических системах аn = 1 + К, а в астатических аn = К, где К — общий коэффициент усиления по разомкнутой цепи регулирования. Следовательно, повышение быстродействия может осуществляться за счет увеличения общего коэффициента усиления.
Для оценки быстродействия системы может использоваться понятие степени устойчивости. (Термин «степень устойчивости» не является удачным, и его, вообще говоря, следовало заменить термином «степень быстродействия». Это объясняется тем, что «степень устойчивости» никак не связана с удалением системы от границы устойчивости, определяемым по склонности системы к колебаниям. Однако этот термин используется в литературе, и мы будем его придерживаться.)
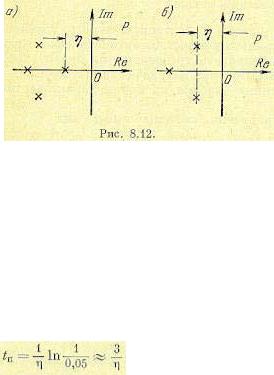
Под степенью устойчивости η понимается абсолютное значение вещественной части ближайшего к мнимой оси корня (рис. 8.12). Здесь могут быть два случая: когда ближайший корень является вещественным (рис. 8.12, а) и когда к оси мнимых ближе всего расположена пара комплексных корней (рис. 8.12, б).
Корни характеристического уравнения, расположенные ближе всего к оси мнимых, т. е. имеющие наименьшую по абсолютной величине вещественную часть, дают в переходном процессе (7.3) члены, которые затухают наиболее медленно. В большинстве случаев переходный процесс можно считать закончившимся тогда, когда затухнет член, определяемый ближайшим к мнимой оси корнем. Если ближайшим к мнимой оси является вещественный корень, то составляющая в переходном процессе, определяемая этим корнем, будет иметь вид
Положив в конце переходного процесса  , где ∆ = 0,01-0,05, можно получить приближенную зависимость между степенью устойчивости и временем переходного процесса:
, где ∆ = 0,01-0,05, можно получить приближенную зависимость между степенью устойчивости и временем переходного процесса:
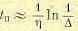 (8.30)
(8.30)
Так, например, если принять ∆ = 0,05, то время переходного процесса составит
Если ближайшей к оси мнимых является пара комплексных корней  , то составляющая в переходном процессе, определяемая этими корнями,
, то составляющая в переходном процессе, определяемая этими корнями,
будет . Положив в этом случае
. Положив в этом случае  , нельзя в общем виде определить время переходного процесса, так как для этой цели потребовалось бы решить
, нельзя в общем виде определить время переходного процесса, так как для этой цели потребовалось бы решить
трансцендентное уравнение. Однако можем найти верхнюю границу переходного процесса, положив в этом уравнении . Тогда получим выражение
. Тогда получим выражение
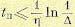 (8.31)
(8.31)
Таким образом, и в этом случае величина степени устойчивости будет в какой-то мере определять быстроту затухания переходного процесса.
Более строго связь между видом переходного процесса и величиной степени "устойчивости может быть определена для случая, когда исходное дифференциальное уравнение системы имеет вид
 (8.32)
(8.32)
Тогда можно показать [61], что при всех вещественных корнях или одной паре комплексных корней для переходной функции справедливо неравенство
 (8.33)
(8.33)
где 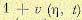 — функция, ограничивающая h(t) сверху (мажоранта);
— функция, ограничивающая h(t) сверху (мажоранта); 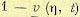 —
—
функция, ограничивающая h(t) снизу (миноранта). Вспомогательная функция 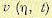 определяется из выражения
определяется из выражения
(8.34)
Миноранта совпадает с переходной функцией, если характеристическое уравнение имеет корень р1 = -η кратности n, т. е. выглядит следующим образом:
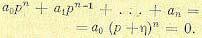 (8.35)
(8.35)
Очевидно, что в этом случае n-кратный корень совпадает со среднегеометрическим
корнем Из неравенства (8.33) вытекает, что при заданном значении среднегеометрического корня
Из неравенства (8.33) вытекает, что при заданном значении среднегеометрического корня
Ω0=const и всех вещественных корнях наименьшее время переходного процесса будет при всех кратных корнях, т. е. в случае (8.35).
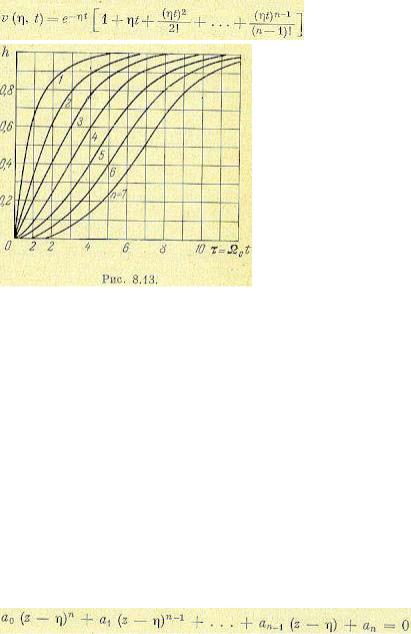
На рис. 8.13 приведены миноранты, совпадающие с переходными характеристиками для случая n-кратного корня, построенные в функции относительного времени 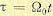 для различных значений порядка дифференциального уравнения n.
для различных значений порядка дифференциального уравнения n.
Важным обстоятельством является то, что степень устойчивости можно найти без вычисления значений корней характеристического уравнения. Для этой цели в характеристическом уравнении (8.25) переходят к новой переменной z = p+η. Подставляя в него p = z-η, получаем так называемое смещенное уравнение
Раскрывая скобки и группируя подобные члены, получаем

 (8.37)
(8.37)
Это уравнение соответствует смещению осей на плоскости корней (рис. 8.12) влево на величину η. В результате один (рис. 8.12, а) или два (рис. 8.12, б) корня попадают на ось мнимых, что соответствует границе устойчивости. Для вычисления степени устойчивости: необходимо применить к смещенному характеристическому уравнению (8.37) любой критерий устойчивости и определить, при каком значении η получается граница устойчивости. Напомним, что апериодической границе устойчивости соответствует равенство нулю свободного члена характеристического уравнения:
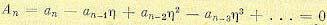 (8.38)
(8.38)
а колебательной границе устойчивости соответствует равенство нулю предпоследнего определителя Гурвица, прохождение кривой Михайлова через начало координат и прохождение амплитудно-фазовой характеристики разомкнутой системы через точку (—1, j0).
Обратимся теперь к оценке запаса устойчивости системы автоматического регулирования. Склонность системы к колебаниям будет наблюдаться, если в решении характеристического
уравнения будут присутствовать комплексные корни вида  . Эта склонность может характеризоваться отношением мнимой части корня (угловой частоты колебаний) к вещественной (коэффициенту затухания), которое называется колебательностью:
. Эта склонность может характеризоваться отношением мнимой части корня (угловой частоты колебаний) к вещественной (коэффициенту затухания), которое называется колебательностью:
 (8.39)
(8.39)
Колебательность связана с другим корневым показателем запаса устойчивости — с так называемым затуханием. Комплексные сопряженные корни дают в выражении для переходного процесса член вида
Найдем затухание амплитуды синусоидального колебания за один период. При некотором времени t=t1 эта амплитуда равна
Через один период 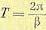
Затуханием за период называют величину
 (8.40)
(8.40)
Эта величина обычно выражается в процентах. Подставляя значение амплитуды С2, получаем
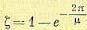 (8.41)
(8.41)
или
 (8.42)
(8.42)
Обычно в системах автоматического регулирования допускается затухание за один период не менее чем 90-98%. Так, например, если ξ% = 98%, то допустимая колебательность при этом составит
Cоответственно при ξ = 90% получаем  .
.
Задание определенной колебательности заставляет ограничивать область расположения корней двумя лучами (рис. 8.14, а), которые составляют с осью вещественных угол
Колебательность системы можно определить без нахождения корней характеристического уравнения подобно тому, как это было сделано выше по отношению к степени устойчивости. Идея метода заключается в том, что используется подстановка  , которая соответствует
, которая соответствует
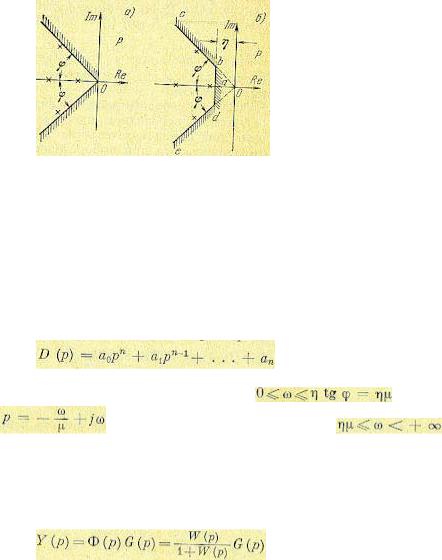
повороту координатных осей (рис. 8.14, б) против часовой стрелки на угол  . При этом по крайней мере один корень попадает на ось мнимых и затем он отыскивается. Ввиду громоздкости этот метод почти не имеет практического значения.
. При этом по крайней мере один корень попадает на ось мнимых и затем он отыскивается. Ввиду громоздкости этот метод почти не имеет практического значения.
При' задании допустимых значений колебательности и степени устойчивости область расположения корней должна ограничиваться также вертикальной прямой, проходящей параллельно оси мнимых на расстоянии η (рис. 8.14, б). Расположению корней в этой области соответствует выдерживание требуемого запаса устойчивости, определяемого величиной колебательности р, или затуханием, и требуемой степени устойчивости η, характеризующей быстродействие системы.
Для |
определения параметров системы, при которых обеспечивается нахождение |
корней |
характеристического уравнения в заданной области, можно воспользоваться D- |
разбиением. В этом случае в плоскости двух параметров системы может быть построена область, аналогично построению области устойчивости (см. §6.4). Напомним, что при построении области устойчивости комплексная величина р = jω изменялась от —∞ до +∞, что соответствует движению по мнимой оси снизу вверх. В рассматриваемом случае комплексная величина р должна перемещаться по границе допустимого расположения корней edabc (рис. 8.14, б). В силу симметрии области достаточно рассмотреть участок abc.
Методика построения допустимой области изменения двух параметров системы А и В, входящих линейно в характеристический полином
остается аналогичной, за тем исключением, что для участка аb делается подстановка p=-η+jω, а
затем частота изменяется в пределах |
. Для участка bс делается подстановка |
и частота изменяется в пределах |
. |
Использование корней характеристического уравнения для оценки качества регулирования |
|
является не совсем полным, так как вид переходного процесса определяется не только левой, но и правой частью дифференциального уравнения. Для того чтобы учесть это обстоятельство, рассмотрим, например, зависимость между регулируемой величиной и управляющим воздействием, записанную посредством передаточной функции замкнутой системы (5.18):
Передаточная функция замкнутой системы представляет собой дробно-рациональную функцию
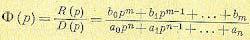 (8.44)
(8.44)
Раскладывая числитель и знаменатель (8.44) на множители, получим
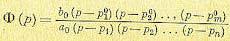 (8.45)
(8.45)
Корни числителя р01, . . ., Р0m называются нулями передаточной функции, так как в точке
 передаточная функция обращается в нуль. Корни знаменателя p1, ..., pn являются корнями характеристического уравнения, и они называются полюсами передаточной функции. В полюсе, т. е. при p = pi, передаточная функция обращается в бесконечность.
передаточная функция обращается в нуль. Корни знаменателя p1, ..., pn являются корнями характеристического уравнения, и они называются полюсами передаточной функции. В полюсе, т. е. при p = pi, передаточная функция обращается в бесконечность.

Полюсы передаточной функции характеризуют левую часть дифференциального уравнения, а нули — правую. В частном случае, когда передаточная функция (8.44) не имеет нулей, правая
часть дифференциального уравнения имеет вид 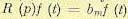 и формула (8.45) сводится к выражению
и формула (8.45) сводится к выражению
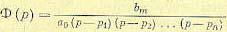 (8-46)
(8-46)
В этом случае вид переходного процесса определяется только расположением полюсов. Задание области расположения полюсов и нулей позволяет более полно оценить вид переходного процесса. Не останавливаясь на подробном анализе, приведем без доказательства общие рекомендации, которых желательно придерживаться при выборе расположения полюсов и
нулей передаточных функций [98].
1.Желательно располагать нули вблизи области расположения полюсов. Удаление нулей от области полюсов ведет к увеличению амплитуд собственных колебаний в переходном процессе.
2.Для уменьшения отклонений в переходном процессе часто бывает выгодно удалять полюсы друг от друга.
3.Приближение друг к другу не представляет опасности для тех полюсов, которые расположены далеко от мнимой оси.
Кроме этих рекомендаций сохраняют свою силу ограничения на область расположения полюсов, накладываемые в связи с требованиями обеспечения определенного запаса устойчивости и быстродействия (см. рис. 8.14, б).
§8.7. Диаграмма Вышнеградского
Рассмотрим характеристическое уравнение третьего порядка
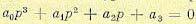 (8.47)
(8.47)
Приведем его к нормированному виду. Для этого разделим все члены на а3 и введем новую переменную
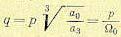 (8.48)
(8.48)
Здесь использовано понятие среднегеометрического корня (8.26):
В результате получим нормированное уравнение
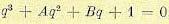 (8.49)
(8.49)
где коэффициенты называются параметрами Вышнеградского.
На плоскости параметров А и В нанесем границу устойчивости. Условия устойчивости системы третьего порядка были впервые сформулированы Вышнеградским еще в 1876 году, до появления в 1895 году критерия Гур-вица. Эти условия: А >0, В >0 и АВ >1. Уравнение границы устойчивости (колебательной): АВ = 1 при А>0 и В >0. Это есть равнобокая гипербола, для которой оси координат служат асимптотами (рис. 8.15). Область устойчивости системы, согласно написанным выше условиям, лежит выше этой кривой.
Разобьем область устойчивости на отдельные части, соответствующие различному расположению корней характеристического уравнения. Заметим, что в точке С, где А = 3 и В = 3,
характеристическое уравнение (8.49) принимает вид 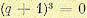 . Следовательно, в этой точке все три корня равны:
. Следовательно, в этой точке все три корня равны:  . При этом для исходного характеристического
. При этом для исходного характеристического
уравнения согласно (8.48) получаем |
. |
В общем случае возможны два варианта: 1) все три корня вещественные; 2) один корень |
|
вещественный и два комплексных. |
|
Граница между этими двумя случаями определяется равенством нулю дискриминанта |
|
уравнения третьей степени (8.49), который может быть получен, |
например, из формулы |
Кардана для решения кубического уравнения 

Это уравнение дает на плоскости параметров А, В две кривые: СЕ и СF (рис. 8.15). Внутри области ЕСF дискриминант положителен. Следовательно, в этой области имеется три вещественных корня (область III). В остальной части плоскости дискриминант отрицателен, что соответствует наличию пары комплексных корней.
Существенное значение имеет взаимное расположение вещественного и комплексных корней. Будем различать здесь два случая: I — пара комплексных корней лежит ближе к мнимой оси, чем вещественный, и II — вещественный корень лежит ближе к мнимой оси, чем пара комплексных. Границей между этими двумя случаями является расположение всех трех корней на одинаковом расстоянии от мнимой оси. Уравнение этой границы можно найти, положив значения корней и
и  . Тогда характеристическое уравнение (8.49) будет
. Тогда характеристическое уравнение (8.49) будет
Уравнивание коэффициентов при одинаковых степенях дает
Врезультате совместного решения последних трех равенств получаем после исключения α
иβ искомое уравнение, соответствующее граничному случаю:
Написанное равенство дает на плоскости параметров кривую СD.
Врезультате область устойчивости разбивается на три части: I, II, III (см. рис. 8.15). Этот график называется диаграммой Вышнеградского. Он построен им в 1876 году в работе, которая положила начало развитию теории автоматического регулирования. На рисунке показан характер расположения корней внутри каждой из этих частей области устойчивости.
Вобласти ///, где все корни вещественные, в зависимости от начальных условий получим апериодический переходный процесс в одной из форм, показанных на третьем графике рис. 8.16. Область /// носит название области апериодических процессов.
Вобластях / и //, где имеется один вещественный корень и два комплексных, переходный процесс будет иметь соответственно формы, показанные на первых двух графиках рис. 8.16. В области /быстрее затухает экспонента и переходный процесс в основном будет определяться колебательной составляющей.
Это будет область колебательных процессов. В области //, наоборот, быстрее затухает колебательная составляющая. Это будет область монотонных процессов.
