
Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975
.pdf
Оказывается, что кривая Михайлова для устойчивых систем всегда имеет плавную спиралевидную форму, причем конец ее уходит в бесконечность в том квадранте комплексной плоскости, номер которого равен степени характеристического уравнения п (рис. 6.8). Число квадрантов, большее чем n, кривая Михайлова вообще не может пройти. Поэтому неустойчивость системы всегда связана с тем, что в кривой Михайлова нарушается последовательность прохождения квадрантов, вследствие чего угол поворота
вектора 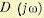 оказывается меньшим чем
оказывается меньшим чем 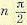 (рис. 6.9).
(рис. 6.9).
Сказанное выше позволяет сформулировать критерий Михайлова в несколько измененном виде. Для устойчивой системы кривая Михайлова проходит последовательно п квадрантов. Поэтому корни уравнений X (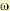 ) = = 0 и У (
) = = 0 и У ( ) = 0 должны чередоваться. Так как кривая Михайлова всегда начинается с точки, расположенной на оси вещественных (рис. 6.8), где мнимая часть обращается в нуль: У (
) = 0 должны чередоваться. Так как кривая Михайлова всегда начинается с точки, расположенной на оси вещественных (рис. 6.8), где мнимая часть обращается в нуль: У (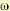 1) = У (0) = 0, то при постепенном увеличении частоты от нуля до бесконечности должна обратиться в нуль сначала вещественная часть: X (
1) = У (0) = 0, то при постепенном увеличении частоты от нуля до бесконечности должна обратиться в нуль сначала вещественная часть: X (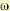 2) — 0? затем мнимая: У (
2) — 0? затем мнимая: У ( 3) = 0, затем опять вещественная:
3) = 0, затем опять вещественная:
X( 4) = 0 и т. д., причем 0 =
4) = 0 и т. д., причем 0 =  <
< 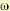 2 <
2 < 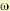 3 <
3 < 4 < . . . . ... <
4 < . . . . ... <  n.
n.
По кривой Михайлова можно судить о том, сколько корней с положительными вещественными частями содержит характеристическое уравнение данной неустойчивой системы. Для нахождения искомого числа l должна использоваться зависимость (6.23).
Если известны результирующий угол поворота вектора  и степень характеристического уравнения n, то в уравнении (6.23) неизвестным будет только l.
и степень характеристического уравнения n, то в уравнении (6.23) неизвестным будет только l.
При подсчете результирующего угла поворота  следует иметь в виду, что при четной степени уравнения кривая Михайлова стремится к бесконечности параллельно оси X и при нечетной степени — параллельно оси У. Это видно из выражений (6.18) и (6.19), так как при четной степени наивысшая степень
следует иметь в виду, что при четной степени уравнения кривая Михайлова стремится к бесконечности параллельно оси X и при нечетной степени — параллельно оси У. Это видно из выражений (6.18) и (6.19), так как при четной степени наивысшая степень  будет стоять в выражении X, а. при нечетной — в выражении У.
будет стоять в выражении X, а. при нечетной — в выражении У.
Так, например, для кривой, показанной на рис. 6.9 и соответствующей n = 3, результирующий угол поворота
Отсюда имеем
и число корней в правой полуплоскости l = 2.
Наличие границы устойчивости всех трех типов может быть определено по 'кривой Михайлова следующим образом.
В случае границы устойчивости первого типа (нулевой корень) отсутствует свободный член характеристического полинома аn = 0 и кривая Михайлова идет из начала координат (рис. 6.10, а).
При границе устойчивости второго типа (колебательная граница устойчивости) левая часть характеристического уравнения, т. е. характеристический полином, обращается в
нуль при подстановке  :
:
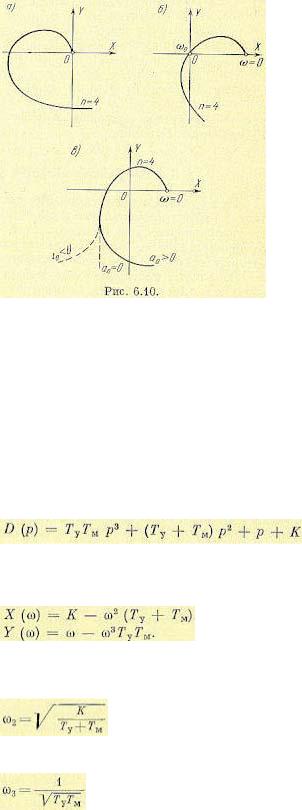
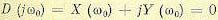 (6.24)
(6.24)
откуда вытекают два равенства:
 (6.25)
(6.25)
Это значит, что точка  на кривой Михайлова попадает в начало координат (рис. 6.10, б). При этом величина
на кривой Михайлова попадает в начало координат (рис. 6.10, б). При этом величина 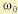 есть частота незатухающих колебаний системы.
есть частота незатухающих колебаний системы.
Для границы устойчивости третьего типа (бесконечный корень) конец кривой Михайлова перебрасывается, как показано на рис. 6.10, в. При этом коэффициент а0 характеристического полинома (6.16) будет проходить через нулевое значение, меняя знак плюс на минус.
Необходимо помнить, что все остальные корни характеристического уравнения должны иметь отрицательные вещественные части. Графически это выражается в том, что в первых двух случаях после малой деформации кривой Михайлова около начала координат (рис. 6.10), а в третьем случае при малом a0 > 0 кривая Михайлова должна удовлетворять критерию устойчивости.
Применим критерий Михайлова для определения устойчивости рассмотренной в предыдущем параграфе следящей системы (рис. 6.4). Из полученного характеристического уравнения определяем характеристический полином
и характеристический комплекс
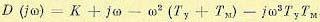 .
.
Вещественная и мнимая части:
Примерный вид кривой Михайлова для этого случая изображен на рис. 6.11.
Найдем условие устойчивости из требования чередования корней 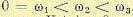 Корень
Корень  2 находится из уравнения X (
2 находится из уравнения X ( ) = 0:
) = 0:
Отсюда имеем первое условие устойчивости К >0. Корень  3 находится из уравнения У (
3 находится из уравнения У ( ) = 0:
) = 0:
Подставляя эти значения в требуемое условие, получаем второе условие устойчивости системы
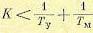
которое, конечно, совпадает с полученным ранее условием устойчивости по критерию Гурвица.
§ 6.4. Построение областей устойчивости. D-разбиение
При расчете и проектировании системы автоматического регулирования иногда бывает необходимым исследовать влияние ее различных параметров на устойчивость. Для решения этой задачи служит построение областей устойчивости, т. е. определение таких областей значений параметров, при которых система оказывается устойчивой.
Различают построение областей устойчивости в плоскости одного параметра и в плоскости двух параметров. Ниже будет рассматриваться только построение областей устойчивости в плоскости двух параметров. Для построения таких областей на плоскости двух параметров А и В необходимо нанести линии, соответствующие границе устойчивости. Тогда область, ограниченная этими линиями, будет представлять собой область устойчивости. Для того чтобы окончательно убедиться в этом, необходимо для любой точки, лежащей внутри полученной области, по какому-либо критерию проверить устойчивость. Если устойчивость для этой точки будет иметь место, то она будет выполняться и для всех других точек, лежащих в этой области.
Для построения границ области устойчивости используются все три признака существующих типов границы устойчивости. Для границы устойчивости первого типа это будет равенство аn = 0. Для границы устойчивости третьего типа — равенство а0= 0.
Для получения условия, соответствующего границе устойчивости второго типа (колебательной), можно использовать различные критерии устойчивости.
Для систем, описываемых уравнением не выше четвертого порядка, может применяться критерий Гурвица. В этом случае колебательной границе устойчивости соответствует равенство нулю предпоследнего определителя Гурвица:  .
.
Для уравнений любого порядка удобно использовать критерий Михайлова. Колебательной границе устойчивости в этом случае соответствует равенство нулю характеристического комплекса  , т. е. прохождение кривой Михайлова через начало координат.
, т. е. прохождение кривой Михайлова через начало координат.
Предположим, что два рассматриваемых параметра системы регулирования А и В входят линейно в характеристический комплекс. Тогда для границы устойчивости
колебательного типа уравнение  распадается на два уравнения:
распадается на два уравнения:
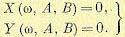 (6.26)
(6.26)
Здесь величина ю дает значение чисто мнимого корня, т. е. частоту гармонических колебаний системы.
Два последних выражения представляют собой параметрические уравнения границы устойчивости при соблюдении дополнительного условия отрицательности вещественных частей всех остальных корней, кроме чисто мнимых. Полная же совокупность всех кривых на плоскости параметров, разбивающая всю плоскость на области с определенным распределением корней, называется D-разбиением плоскости параметров. Обычно практическое значение имеет лишь часть кривых D-разбиения, соответствующая границе устойчивости.
Для упрощения выделения границ области устойчивости из всего комплекса кривых D-разбиения на плоскости двух параметров вводится штриховка этих кривых, производимая по правилу, которое будет приведено без доказательства. Перемещаясь вдоль кривой в сторону увеличения со, надо штриховать ее с левой стороны, если будет положительным определитель, составленный из частных производных (6.26):
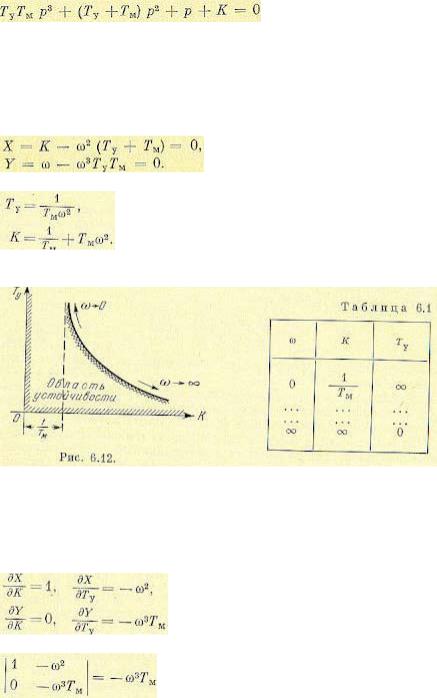
 (6.27)
(6.27)
Если же определитель отрицателен, то кривую надо штриховать справа. При соблюдении этого правила штриховка будет направлена внутрь области устойчивости, если параметр А отложен по оси абсцисс вправо, а параметр В — по оси ординат вверх.
В качестве иллюстрации рассмотрим следящую систему, схема которой изображена на рис. 6.4. Для этой системы было получено характеристическое уравнение
Предположим, что электромеханическая постоянная времени двигателя Тм является заданной величиной и требуется построить область устойчивости в плоскости двух параметров: общего коэффициента усиления К и постоянной времени усилителя Ту.
Характеристический комплекс
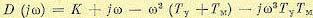 .
.
Уравнения, определяющие границу устойчивости,
Решая их совместно относительно параметров К и Tу, получим
Задаваясь затем различными значениями ω в пределах от нуля до бесконечности, по этим формулам можно вычислить значения искомых параметров
и составить табл. 6.1, одинаковую для положительных и отрицательных частот. По полученным данным строим кривую D-разбиения (рис. 6.12). Кривая имеет
гиперболический вид с асимптотами  при ω = 0 и Ту =0, при
при ω = 0 и Ту =0, при 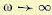 .
.
Для нанесения штриховки найдем знак определителя (6.27). Необходимые для этого частные производные будут при А = К и В = Tу:
Определитель получается равным
Для отрицательных частот, т. в. при изменении частоты в пределах от  до 0, полученный определитель будет положительным. Поэтому при движении по полученной кривой снизу вверх (от
до 0, полученный определитель будет положительным. Поэтому при движении по полученной кривой снизу вверх (от  до 0) необходимо штриховать область, лежащую слева от кривой.
до 0) необходимо штриховать область, лежащую слева от кривой.
Для положительных частот, т. е. при изменении частоты в пределах от 0 до 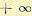 , полученный определитель будет отрицательным. Поэтому при движении по полученной
, полученный определитель будет отрицательным. Поэтому при движении по полученной

кривой сверху вниз (от 0 до 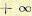 ) необходимо штриховать область, лежащую справа от кривой. Снизу полученной кривой получится двойная штриховка.
) необходимо штриховать область, лежащую справа от кривой. Снизу полученной кривой получится двойная штриховка.
Область устойчивости практически уже сформировалась. Так как параметры К и Ту должны быть положительными, область устойчивости будет ограничиваться полученной кривой и положительными направлениями осей К и Tу.
Это можно показать и на основе использования двух оставшихся условий устойчивости. Граница устойчивости первого типа будет получена, если приравнять нулю свободный член, аn = 0, что дает условие К = 0. Это условие выполняется на оси ординат. Граница устойчивости третьего типа получается при а0 = 0, что дает условие Ту = 0. Это условие выполняется на оси абсцисс.
Таким образом, область устойчивости в плоскости параметров К и Ту получена окончательно. Для любых значений К и Tу можно сразу ответить, устойчива или неустойчива система, смотря по тому, попадает или не попадает точка, определяемая этими значениями параметров, в область устойчивости.
§6.5. Критерий устойчивости Найквиста
Вглаве 5 было введено понятие передаточной функции разомкнутой системы. Эта функция может быть представлена в виде
 (6.28)
(6.28)
причем степень числителя не может быть выше степени знаменателя, 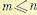 . При подстановке
. При подстановке  получается частотная передаточная функция разомкнутой системы
получается частотная передаточная функция разомкнутой системы
 (6.29)
(6.29)
Частотная передаточная функция разомкнутой системы представляет собой комплексное число. На основании рассмотренных в главе 4 частотных характеристик смысл ее можно объяснить следующим образом (рис. 6.13). Представим себе систему регулирования в разомкнутом состоянии в виде некоторого звена с передаточной функцией W(р). Если на вход этого звена подавать сигнал ошибки в виде гармонических
колебаний  с амплитудой Xmах и частотой ω, то в установившемся режиме на выходе регулируемая величина будет изменяться также по гармоническому закону
с амплитудой Xmах и частотой ω, то в установившемся режиме на выходе регулируемая величина будет изменяться также по гармоническому закону
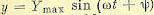 с амплитудой Уmах той же частотой со и фазовым сдвигом
с амплитудой Уmах той же частотой со и фазовым сдвигом 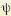 . Модуль частотной передаточной функции представляет собой отношение амплитуд выходной и входной величин:
. Модуль частотной передаточной функции представляет собой отношение амплитуд выходной и входной величин:
а аргумент — сдвиг фаз 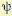 .
.
Если изменять частоту входного воздействия от и откладывать на комплексной плоскости точки, соответствующие получающимся комплексным числам, то геометрическое место этих точек образует амплитудно-фазовую характеристику разомкнутой системы (рис. 6.14).
Ветвь этой характеристики, соответствующая отрицательным частотам, является зеркальным отражением ветви, соответствующей положительным частотам, относительно вещественной оси.
На амплитудно-фазовой характеристике для удобства могут отмечаться точки, соответствующие определенным частотам, например ω1, ω 2, ω3 и т.д. Вдоль кривой иногда рисуют стрелки, которые показывают направление возрастания частоты ω (рис. 6.14).
В реальных системах всегда удовлетворяется условие m < n. Поэтому при частоте, стремящейся к бесконечности, модуль частотной передаточной функции стремится к
нулю и точка с частотой  попадает в начало координат.
попадает в начало координат.
Сформулируем достаточные и необходимые требования к амплитудно-фазовой характеристике разомкнутой системы, при выполнении которых система автоматического регулирования в замкнутом состоянии будет устойчивой.
Ограничим вначале задачу и будем рассматривать только такие передаточные функции (6.28), которые соответствуют статическим системам. Это значит, что знаменатель (6.28) не будет иметь в качестве множителя оператор р. Кроме того, будем пока рассматривать только устойчивые в разомкнутом состоянии системы. Это значит, что полюсы выражения (6.28), т. е. корни уравнения
 (6.30)
(6.30)
лежат в левой полуплоскости.
Введем в рассмотрение вспомогательную функцию
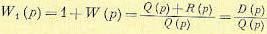 (6.31)
(6.31)
где числитель
 (6.32)
(6.32)
представляет собой характеристический полином системы. Сделаем подстановку  и найдем комплекс
и найдем комплекс
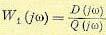 (6.33)
(6.33)
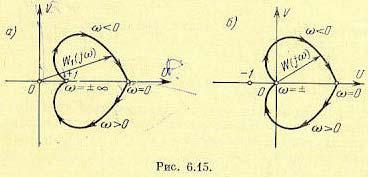
Будем теперь изменять частоту от  и изобразим получившуюся амплитудно-фазовую характеристику
и изобразим получившуюся амплитудно-фазовую характеристику  на комплексной плоскости (рис. 6.15, а). Рассмотрим результирующий угол поворота вектора
на комплексной плоскости (рис. 6.15, а). Рассмотрим результирующий угол поворота вектора  при изменении частоты от
при изменении частоты от  . Этот угол представляет собой изменение аргумента (6.33), который по
. Этот угол представляет собой изменение аргумента (6.33), который по
правилу деления комплексных чисел равен разности аргументов числителя  и знаменателя
и знаменателя  :
:
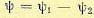 .
.
Числитель (6.33) представляет собой характеристический комплекс. Если все корни характеристического уравнения лежат в левой полуплоскости, то при изменении частоты от  аргумент
аргумент 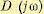 изменится на величину
изменится на величину  , где n — степень
, где n — степень

характеристического полинома. При построении кривой Михайлова результирующий
угол поворота был равен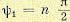 , но там частота изменялась от 0 до
, но там частота изменялась от 0 до  . Знаменатель (6.33) представляет собой комплекс той же степени n, причем по
. Знаменатель (6.33) представляет собой комплекс той же степени n, причем по
предположению все корни (6.30) лежат в левой полуплоскости.
Поэтому результирующий угол поворота вектора  при изменении частоты от
при изменении частоты от 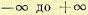 будет равен
будет равен  .
.
Отсюда следует, что в рассматриваемом случае результирующий угол поворота вектора  будет равен нулю:
будет равен нулю:  . Это означает, что для устойчивой в замкнутом состоянии системы годограф вектора
. Это означает, что для устойчивой в замкнутом состоянии системы годограф вектора 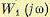 не должен охватывать начала координат (рис. 6.15, а).
не должен охватывать начала координат (рис. 6.15, а).
Частотная передаточная функция  отличается от вспомогательной функции
отличается от вспомогательной функции 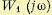 на единицу. Поэтому можно строить амплитудно-фазовую характеристику разомкнутой системы по выражению (6.29), что проще. Но в этом случае амплитуднофазовая характеристика не должна охватывать точку с координатами (— 1, j0). Это является достаточным и необходимым условием того, чтобы система была устойчивой в замкнутом состоянии (рис. 6.15, б).
на единицу. Поэтому можно строить амплитудно-фазовую характеристику разомкнутой системы по выражению (6.29), что проще. Но в этом случае амплитуднофазовая характеристика не должна охватывать точку с координатами (— 1, j0). Это является достаточным и необходимым условием того, чтобы система была устойчивой в замкнутом состоянии (рис. 6.15, б).
При определении устойчивости достаточно построить амплитудно-фазовую характеристику только для положительных частот, так как ее ветвь, соответствующая отрицательным частотам, может^быть легко получена зеркальным отображением относительно оси вещественных.
На рис. 6.16, а изображен случай так называемой абсолютно устойчивой системы. Этот термин означает, что система остается устойчивой при любом уменьшении коэффициента усиления разомкнутой цепи. Напомним, что передаточная функция разомкнутой статической системы может быть представлена в виде
Нетрудно видеть, что уменьшение общего коэффициента усиления К приводит к уменьшению модуля (6.29), а это в случае, изображенном на рис. 6.16, а, не может привести к охвату годографом точки (—1, j0).
На рис. 6.16, б изображен случай так называемой условно устойчивой системы. Здесь система будет устойчивой при значении общего коэффициента усиления, лежащем в некоторых пределах. Как увеличение, так и уменьшение общего коэффициента усиления К может привести к охвату годографом точки (—1, j0), что будет соответствовать неустойчивости системы в замкнутом состоянии.
На рис. 6.16, в изображен случай, когда система находится на границе устойчивости. Граница устойчивости будет колебательного типа. Это вытекает из того, что при
некоторой частоте, при которой годограф пересекает точку (—1, jО), имеет место равенство 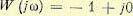 , что может быть записано в виде
, что может быть записано в виде
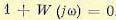 .
.
Последнее выражение представляет собой характеристическое уравнение, которое обращается в нуль при подстановке  . Таким образом, чисто мнимый корень является решением характеристического уравнения.
. Таким образом, чисто мнимый корень является решением характеристического уравнения.
На рис. 6.16, г изображен случай неустойчивой системы.
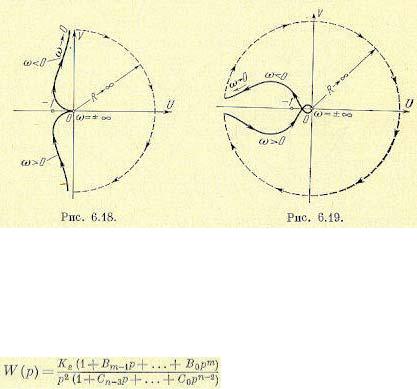
Обратимся теперь к передаточной функции разомкнутой системы, соответствующей астатизму первого порядка. В этом случае передаточная функция может быть изображена в виде
Будем предполагать, что все корни знаменателя передаточной функции (кроме нулевого корня р = 0) лежат в левой полуплоскости, т.е. в разомкнутом состоянии система является нейтрально устойчивой.
Амплитудно-фазовая характеристика разомкнутой системы будет иметь разрыв непрерывности в точке  .
.
В этой точке модуль  , а фаза делает скачок на 180°. Для получения определенности в ходе амплитудно-фазовой характеристики необходимо отнести нулевой корень знаменателя передаточной функции Тy (р) либо к левой, либо к правой полуплоскости корней (рис. 6.3). Первое является более удобным, так как при этом все корни знаменателя Тy (р) будут расположены в левой полуплоскости.
, а фаза делает скачок на 180°. Для получения определенности в ходе амплитудно-фазовой характеристики необходимо отнести нулевой корень знаменателя передаточной функции Тy (р) либо к левой, либо к правой полуплоскости корней (рис. 6.3). Первое является более удобным, так как при этом все корни знаменателя Тy (р) будут расположены в левой полуплоскости.
Для выполнения сказанного поступают следующим образом. При изменении частоты от  происходит движение на плоскости корней вдоль оси мнимых снизу вверх (рис. 6.17). В начале координат расположен нулевой корень. Обойдем этот корень по полуокружности бесконечно малого радиуса так, чтобы корень остался слева. При движении по этой полуокружности против часовой стрелки независимая переменная р меняется по закону
происходит движение на плоскости корней вдоль оси мнимых снизу вверх (рис. 6.17). В начале координат расположен нулевой корень. Обойдем этот корень по полуокружности бесконечно малого радиуса так, чтобы корень остался слева. При движении по этой полуокружности против часовой стрелки независимая переменная р меняется по закону
где 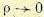 представляет собой радиус полуокружности, а
представляет собой радиус полуокружности, а  — аргумент,
— аргумент,
меняющийся от  . При этом передаточная функция Тy (р) может быть представлена в виде
. При этом передаточная функция Тy (р) может быть представлена в виде
где  , а аргумент (
, а аргумент ( ) меняется в пределах от
) меняется в пределах от  .
.
Таким образом, во время движения по полуокружности бесконечно малого радиуса передаточная функция может быть представлена в виде вектора бесконечно большой длины, поворачивающегося на комплексной плоскости по часовой стрелке на угол,
равный 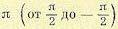 , что соответствует полуокружности бесконечно большого радиуса.
, что соответствует полуокружности бесконечно большого радиуса.
На рис. 6.18 изображена амплитудно-фазовая характеристика абсолютно устойчивой системы с астатизмом первого порядка. Характеристика начинается в начале координат при 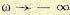 и затем уходит в бесконечность при
и затем уходит в бесконечность при  (верхняя ветвь). Далее характеристика дополняется полуокружностью бесконечно большого радиуса так, чтобы вектор
(верхняя ветвь). Далее характеристика дополняется полуокружностью бесконечно большого радиуса так, чтобы вектор 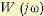 повернулся по часовой стрелке на угол
повернулся по часовой стрелке на угол  . Нижняя ветвь характеристики соответствует изменению частоты от 0 до
. Нижняя ветвь характеристики соответствует изменению частоты от 0 до 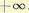 .
.
Нетрудно видеть, что характеристика не охватывает точку (—1, j0), и система в замкнутом состоянии будет устойчивой.
Амплитудно-фазовые характеристики для условно устойчивой системы, для случая колебательной границы устойчивости и случая неустойчивой системы будут похожими на изображенные на рис. 6.16, б, в и г кривые, за тем исключением, что при  характеристика будет уходить в бесконечность в соответствии с нижней ветвью характеристики, изображенной на рис. 6.18.
характеристика будет уходить в бесконечность в соответствии с нижней ветвью характеристики, изображенной на рис. 6.18.
Аналогичными рассуждениями можно показать, что для системы с астатизмом второго порядка, имеющей передаточную функцию вида
при обходе двойного нулевого корня в начале координат (см. рис. 6.17) передаточная функция разомкнутой системы может быть представлена вектором бесконечно большой длины, поворачивающимся по часовой стрелке на угол  .
.
На рис. 6.19 изображена амплитудно-фазовая характеристика абсолютно устойчивой системы при наличии астатизма второго порядка. Так же как и ранее, здесь можно получить условную устойчивость (рис. 6.19), колебательную границу устойчивости, если характеристика пройдет через точку (— 1, j0), и неустойчивость, если характеристика будет охватывать точку (—1, j0).
Обобщая проведенные рассуждения, получаем, что для определения устойчивости системы с астатизмом любого порядка достаточно построить только одну ветвь амплитудно-фазовой характеристики, соответствующую положительным частотам, которая должна быть дополнена окружностью бесконечно большого радиуса. При этом для устойчивой в замкнутом состоянии системы эта ветвь вместе с частью окружности, заключенной между положительной полуосью вещественных и амплитудно-фазовой характеристикой, соответствующей положительным частотам, не должна охватывать точку (—1, j0) в соответствии с рис. 6.20.
Из рис. 6.20 следует, что абсолютная устойчивость может быть получена при степени астатизма 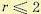 . При большей степени астатизма может быть получена только условная устойчивость.
. При большей степени астатизма может быть получена только условная устойчивость.

Обратимся теперь к более общему случаю, когда знаменатель передаточной функции разомкнутой системы с любой степенью астатизма содержит корни, лежащие в правой полуплоскости. Это соответствует неустойчивой в разомкнутом состоянии системе.
Появление неустойчивости разомкнутой системы может вызываться двумя причинами. Во-первых, это может быть следствием наличия неустойчивых звеньев, подобных рассмотренным в § 4.8. Во-вторых, это может быть следствием потери устойчивости звеньев, охваченных положительными или отрицательными обратными связями (см., например, рис. 5.5).
Наличие неустойчивости системы в разомкнутом состоянии не означает, что система будет неустойчивой в замкнутом состоянии. Она может быть как устойчивой, так и неустойчивой. Однако формулировка критерия устойчивости Найквиста при этом несколько меняется. Пусть знаменатель передаточной функции разомкнутой системы (6.28) содержит l корней в правой полуплоскости и n-l корней — в левой. Тогда при изменении частоты от 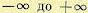 Для устойчивой в замкнутом состоянии системы
Для устойчивой в замкнутом состоянии системы
результирующий угол поворота годографа вектора 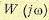 относительно точки ( — 1, j0) должен составить
относительно точки ( — 1, j0) должен составить
т. е. амплитудно-фазовая характеристика должна охватить точку ( — 1, j0) столько раз, сколько корней в правой полуплоскости содержит знаменатель передаточной функции разомкнутой системы. При этом необходимо, чтобы при изменении частоты от
 конец вектора
конец вектора 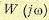 поворачивался вокруг точки ( — 1, j0) на угол
поворачивался вокруг точки ( — 1, j0) на угол  против часовой стрелки. Нетрудно видеть, что формулировка критерия Найквиста для случая, когда l = 0, вытекает отсюда как частный случай.
против часовой стрелки. Нетрудно видеть, что формулировка критерия Найквиста для случая, когда l = 0, вытекает отсюда как частный случай.
Таким образом, при использовании критерия Найквиста, вообще говоря, необходимо убедиться в том, имеются ли в знаменателе передаточной функции разомкнутой системы корни, лежащие в правой полуплоскости, и сколько имеется таких корней.
Если в системе имеются местные обратные связи, например, такого типа, как это изображено на рис. 5.7, то необходимо убедиться в том, что по цепи местной обратной связи не нарушена устойчивость при разомкнутой главной обратной связи. Проверка устойчивости по цепи местной обратной связи может быть сделана посредством использования любых критериев устойчивости, в том числе и посредством критерия Найквиста, который может применяться для разомкнутой местной обратной связи обычным путем построения для этой цели амплитудно-фазовой характеристики.
В случае, если для местной обратной связи будет получено указание на ее неустойчивость, необходимо определить число корней, лежащих в правой полуплоскости.
Следует заметить, что, хотя теоретически вся система в замкнутом состоянии может быть устойчивой при наличии неустойчивости по цепи местной обратной связи,
