Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975

Если задачей обычной самонастройки (с анализатором качества) было сохранение заданного качества системы в некоторых пределах, то задача оптимизатора (т. е. экстремальной настройки параметров регулятора) состоит в том, чтобы в каждый момент времени при меняющихся параметрах объекта настраивать параметры регулятора так, чтобы получать максимум качества, возможный в данных реальных условиях.

Такой оптимизатор должен содержать в себе, следовательно, устройство автоматического поиска экстремума качества (минимум ошибки), подобно поиску экстремального задания регулируемой величины в рассматривавшихся ранее экстремальных системах регулирования. Но особенность оптимизатора здесь состоит не только в специфике той величины, экстремум которой ищется, но главным образом в том, что воздействует он не на настройку требуемого значения регулируемой величины, а на настройку параметров корректирующих устройств самого регулятора.

Самооптимизация (экстремальная самонастройка) является наиболее совершенным, но в то же время и наиболее сложным видом системы с замкнутым контуром самонастройки параметров. В тех случаях, когда самонастройка применяется в системах управления вследствие недостоверности знания свойств объекта, система самооптимизации напоминает процесс самообучения системы 1). Система при этом путем автоматического поиска как бы сама познает неизвестные свойства управляемого объекта

иобучается управлять этим объектом наилучшим образом (сама настраивает параметры регулятора, по экстремуму заданного критерия качества).

Втаких случаях можно поступать следующим образом: запустить указанную сложную самооптимизирующуюся (самообучающуюся) систему в пробную эксплуатацию

идать ей возможность самой настроить параметры регулятора. Затем можно снять устройство самонастройки вовсе и дальше эксплуатировать более простую систему с постоянной или с программной настройкой, выработанной в процессе самооптимизации (самообучения). Это, конечно, не всегда возможно.

Одним из распространенных видов анализаторов и оптимизаторов качества в самонастраивающихся системах являются устройства из операционных усилителей или других математических моделей, построенных на блоках вычислительных машин, которые имитируют желаемое динамическое поведение объекта. Это эталонное качество поведения модели сравнивается с реальным поведением системы, и параметры регулятора настраиваются автоматически и таким образом, чтобы поведение системы «подогнать» к эталонному поведению модели.

На этом же принципе производится «обучение» машины человеком. В самом деле, в качестве эталонной модели можно взять работу человека по управлению, например, процессами в металлургической печи. Можно ввести при этом все те же связи с автоматической системой, которые вводятся в указанной выше самонастраивающейся системе с моделью. Тогда в результате произойдет самонастройка параметров этой системы. Система настроится на работу, дающую те же результаты, которые давала работа человека.

Важная особенность такой системы заключается в том, что здесь не требуется закладывать заранее критерий качества (что требовалось выше), так как он содержится в самом характере действий человека.

При помощи современных средств автоматики и вычислительной техники (включая, конечно, и присущие им логические операции) такого рода сложные задачи для некоторых объектов оказываются вполне осуществимыми. Пока что это делается только для длительно работающих объектов с медленным или с редким скачкообразным изменением параметров, когда процесс самонастройки успевает за темпом изменения свойств объекта. При быстром изменении параметров объекта и окружающих его условий построение таких самонастраивающихся систем является в настоящее время весьма трудной задачей.

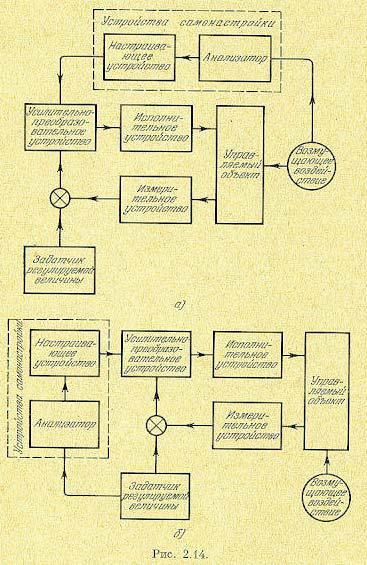
Возможны еще и другие виды систем с самонастройкой параметров регулятора, которые не производят непосредственно анализ или оптимизацию какого-либо показателя качества работы (или ошибки системы), а анализируют форму возмущающего и задаваемого извне управляющего воздействий на систему (рис. 2.14, а) и перенастраивают параметры регулятора в зависимости от формы воздействия по определенному правилу, заложенному заранее в настраивающее устройство. Это — системы с самонастройкой параметров регулятора по возмущению.

.

Применение их выгодно в тех случаях, когда внешнее воздействие может быть измерено с целью анализа его свойств и когда изменение его

формы является решающим для качества работы системы. Часто это имеет место в различного рода следящих системах, особенно когда на вход системы вместе с полезным сигналом поступает помеха. В этом случае для наилучшего воспроизведения полезного сигнала изменяющейся частоты на фоне случайных помех целесообразно было бы менять полосу пропускания ел едящей системы. Это можно сделать, например, путем изменения постоянной времени фильтра в управляющей части указанной следящей системы в зависимости от измеренной частоты поступающего извне сигнала или других свойств сигнала и помехи. В результате вместо обычной следящей системы получится самонастраивающаяся система по возмущению типа представленной на рис. 2.14, б (ее называют часто следящей системой с саморегулированием параметров). При этом анализатор свойств внешнего воздействия может быть, более или менее сложным, основанным на анализе вероятностных характеристик полезного сигнала и помехи.

§ 2.6. Системы с самонастройкой структуры (самоорганизующиеся системы)

Все те же задачи самонастройки и некоторые новые задачи целесообразно бывает решать не путем изменения параметров регулятора, имеющего» определенную структуру, а путем изменения самой структуры регулятора не заданным заранее образом. Это — системы с самонастройкой структуры (самоорганизующиеся системы).

Врассмотренных ранее системах при автоматической настройке параметров регулятора закон регулирования был заранее задан, а менялись не заданным заранее образом лишь входящие в него коэффициенты. Теперь же при автоматической настройке структуры регулятора не задан вообще даже и закон регулирования; в общем случае неизвестно заранее, какие корректирующие устройства и как вводить, какие логические и вычислительные операции производить. В общем случае может меняться структура не только усилительно-преобразовательного, но и измерительного устройства системы управления, если почему-либо выгодно применять разные принципы измерения или же измерять разные исходные величины в разных условиях работы объекта (подобно тому, как человек использует в разных условиях то зрение, то слух, то осязание и т. п. или их комбинированное действие).

Вчастных случаях возможны более простые самоорганизующиеся системы, в которых заранее не задана структура лишь одной небольшой части системы, а структура остальной части задана неизменной. В законе регулирования может быть определено, например, что сигнал по отклонению регулируемой величины обязательно идет по структурно-заданному каналу, а добавляемые сверх этого корректирующие устройства самоорганизуются.

Говоря о самонастройке структуры или, что-то же самое, о самоорганизации, необходимо подчеркнуть, что имеется в виду автоматическое изменение структуры не заданным заранее образом. Это весьма существенно.

Всамом деле, когда рассматривались нелинейные законы регулирования (§ 2.2), уже говорилось, об изменении структуры регулятора. Там могли включаться и отключаться производные и интеграл, могла включаться или переключаться обратная связь и т. п. Но все это делалось хотя и автоматически, но заранее заданным образом в зависимости от значения отклонения регулируемой величины и ее производных. Такое изменение структуры относится не к самоорганизации, а к нелинейным законам регулирования. Нелинейные законы регулирования применяются, в частности, в оптимальных автоматических системах.

Точно так же, если бы структура регулятора менялась программным устройством по определенному заданию во времени, это тоже не относилось бы к самоорганизации, так же как программное изменение параметров, рассматривавшееся в предыдущем параграфе, не относилось к самонастройке параметров.

Равным образом к самоорганизующимся системам не относятся многие существующие измерительные системы, в которых имеется несколько измерительных приборов, основанных на разных принципах измерения одной и той же величины, когда обработка информации от всех этих приборов и их включение и отключение заранее запрограммированы либо во времени, либо в зависимости от размера и скорости изменения измеряемой величины. Вообще же возможна, конечно, и самоорганизация в измерительных системах со многими чувствительными элементами.

Всамоорганизующуюся систему закладывается лишь тот или иной определенный критерий качества работы системы или комбинация критериев для разных внешних условий работы системы. Система сама путем автоматического поиска с применением вычислительных или логических операций выбирает такую структуру (из возможных, имеющихся в ее распоряжении), при которой удовлетворяется заданный критерий качества работы всей системы. Это делается путем подключения и отключений различных

звеньев в некоторой логической последовательности с фиксированием (запоминанием) более удачных структур.

При любой самонастройке и, особенно при самоорганизации может быть учтено требование повышения надежности и предусмотрена возможность работы системы при выходе из строя каких-либо звеньев.

Всамоорганизующейся системе, как и прежде, должен быть либо анализатор, либо оптимизатор качества. Анализатор ставится, когда нужно обеспечить просто заданное в определенных пределах качество. Оптимизатор же предназначается для отыскания и осуществления максимально возможного в данной системе (при данных реальных условиях ее работы) качества.

Вкрупном плане общую схему системы можно представить в таких же вариантах, как на рис. 2.11 и 2.12, но только не с настраивающим устройством, а с логической схемой переключения отдельных звеньев системы в соответствии с сигналами анализатора или оптимизатора. В качестве анализатора здесь тоже может применяться, в частности, математическая эталонная модель объекта с желаемыми свойствами.

Замена такой модели действиями человека позволяет и здесь производить как бы обучение машины человеком. Это совершенно аналогично той картине процесса обучения, которая была описана выше в связи с самонастройкой параметров, но здесь имеет место, образно говоря, более высокий уровень, обучения.

Как и прежде, здесь в ряде случаев возможна установка на объект самоорганизующейся системы регулирования лишь в начальный период его эксплуатации. Затем самоорганизующаяся система может быть снята и заменена более простой системой с определенной структурой или со структурой, меняющейся по программе, которая была автоматически выработана в процессе работы самоорганизующейся системы.

Очевидно, что при прочих равных условиях самоорганизация, т. е. автоматический поиск наивыгоднейшей структуры системы по результатам анализа или оптимизации качества ее работы; является процессом более сложным и более длительным, чем самонастройка параметров, а потому пока что значительно более далеким от применения

кавтоматическому управлению динамическими объектами, где не только поиск, но и сам по себе анализ качества работы требует некоторого промежутка времени. Поэтому здесь опять-таки речь может идти в настоящее время об объектах, работающих в более или менее стационарных условиях, изменяющихся либо медленно, либо редкими скачками.

Как уже отмечалось, к экстремальным и самонастраивающимся системам применяются также термины адаптивные или «приспосабливающиеся» системы и системы с автоматической оптимизацией (в том случае, когда автоматическая оптимизация используется не в процессе проектирования, а в самой системе регулирования или управления в процессе ее эксплуатации). Кроме рассмотренных выше существуют различные другие аспекты самоорганизации, самообучения и т. п., которые рассматриваются в литературе по кибернетике; изучающей наиболее общие законы управления и преобразования информации в автоматических системах, в системах связи, в вычислительных и других машинах, а также и в живых организмах с общей точки зрения. Чем дальше развивается автоматика в технике и познания в биологии, тем больше появляется аналогий функционирования автоматических систем и живых организмов, в том числе системы нервной высшей деятельности и головного мозга человека. Изучение этих аналогий, рассматриваемых с общей кибернетической точки зрения, оказывается очень полезным как для техники, так и для биологии. В частности, техника автоматизации еще далеко не полностью использует возможности нелинейных законов регулирования, самонастройки, самоорганизации и высокой надежности, которые имеют место в процессах управления и преобразования информации в живых организмах.

Вцелом ряде систем управления техническими объектами в качестве «звена» замкнутой системы участвует человек-оператор. В связи с этим развивается новая важная

область технической кибернетики, называемая инженерной психологией, которая изучает проблемы взаимодействия человека-оператора с автоматикой в системах управления и преобразования информации. Это приобретает теперь особенно важное значение не только в процессах управления производством, но также и в связи с совершенствованием процессов управления скоростными самолетами и в связи с развитием космических полетов.

В заключение отметим, что техническая реализация самонастраивающихся и самоорганизующихся систем регулирования и управления в большинстве случаев сложнее, чем систем с нелинейными законами регулирования. Но при этом и возможности самонастраивающихся систем значительно шире. Однако инженер должен иметь в виду, что во многих случаях при помощи нелинейных законов регулирования, проще реализуемых на практике, можно успешно решать ряд таких задач, которые с точки зрения линейной теории регулирования считаются требующими самонастройки как неразрешимые в рамках этой линейной теории.

Р А 3 Д ЕЛ II

ОБЫКНОВЕННЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

ГЛАВА 3

ЛИНЕАРИЗАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

§ 3.1. Линеаризация уравнений

При составлении дифференциальных уравнений динамики любой автоматической системы последнюю разбивают на отдельные звенья и записывают уравнение каждого звена в отдельности. Уравнения всех звеньев образуют единую систему, которую можно преобразовать к одному уравнению путем исключения промежуточных переменных.

Уравнение звена должно быть составлено так, чтобы оно выражало зависимость (в динамическом процессе) между теми величинами, которые в схеме исследуемой системы указаны на выходе и входе данного звена, т. е. между величинами, представляющими воздействие данного звена на последующее по схеме звено и воздействие предыдущего звена на данное. Динамическое уравнение отдельного звена составляется по правилам соответствующей технической науки (звено может представлять собой тепловой двигатель, электрическую машину, механическую передачу, электрическую цепь, ламповую схему и т. п.).

Звено может иметь иногда не одну входную величину, а несколько (например, при наличии дополнительных обратных связей). Кроме входной и выходной величин звена, которые выражают собой внутренние связи между звеньями данной системы, может учитываться также внешнее воздействие.

.

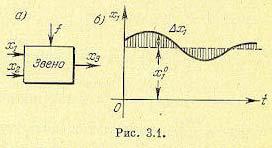
Пусть, например, звено (рис. 3.1, а) какой-нибудь автоматической системы имеет входные величины х1, х2, выходную — х3 и внешнее воздействие f, а динамическое уравнение звена имеет произвольный нелинейный вид

F (x1 , x2 , x2 , x3 , x3 , x3 , x3 ) = ϕ( f , f ) (3.1)

(для примера взят определенный порядок входящих в уравнение производных х2, х3, f; вообще же здесь могут быть любые другие варианты).

Допустим, что установившийся процесс в системе имеет место при некоторых

установившегося состояния для данного звена согласно (3.1) будет

F (x10 , x20 ,0, x30 ,0,0,0) =ϕ( f 0 ,0) (3.2).

В основе линеаризации нелинейных уравнений лежит предположение о том, что в исследуемом динамическом процессе переменные (в данном случае х1, x2, х3) изменяются так, что их отклонения от установившихся значений (х10, х20, x30) остаются все время достаточно малыми (рис. 3.1, б).

2) неизвестными функциями времени в этом уравнении являются не прежние полные величины х1, х2, х3, а их отклонения ∆x1 , ∆x2 , ∆x3 от некоторых установившихся

регулировании).

.

Таким образом, цель получения линейного дифференциального уравнения взамен прежнего нелинейного достигнута. Уравнение (3.5) называется дифференциальным уравнением звена в отклонениях. Проделав то же самое для всех звеньев систе-мы, получим в результате

линеаризованные уравнения процесса регулирования в отклонениях как называют еще, уравнения «в вариациях»).

В дальнейшем можно будет проводить линеаризацию нелинейных уравнений непосредственно по аналогии с формулой (3.5), не производя предварительных выкладок.

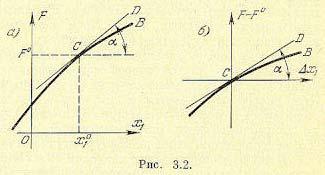
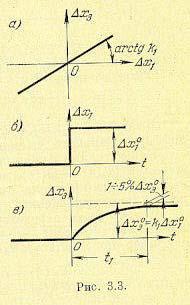
Приведем геометрическую трактовку этого способа линеаризации. Изобразим графически зависимость F от х1 при постоянных значениях всех остальных переменных:

x2 = x20 , x2 = x20 , x3 = x30 , x3 = x3 = x3 = 0

Пусть эта зависимость имеет вид кривой, представленной на рис. 3.2, а. Отметим значение x10 и проведем в точке С касательную. Тогда

∂F 0 = tga , (3.6)∂x1

где a — угол наклона касательной в точке С( x10 ,F0), для которой

x1 = x10

аналитически, здесь эквивалентны переносу начала координат в точку С (рис. 3.2, а), в результате чего получается график рис. 3.2, б.

Первый член линейного уравнения (3.5) согласно (3.6) означает, что линеаризация уравнения геометрически может трактоваться как замена первоначальной кривой СВ на касательную к ней прямую СD. Из графика рис. 3.2, б очевидно, что эта замена тем точнее, чем меньшие величины отклонения ∆x1 возникают в исследуемом динамическом

процессе (основная предпосылка для линеаризации); границы отклонений ∆x1 , для которых допустима линеаризация, тем шире, чем ближе кривая СВ к прямой СD.

Последним обстоятельством и определяются практически в каждой задаче те границы, внутри которых отклонения можно считать «достаточно малыми».

В ряде задач отличие от линейности, показанное на рис. 3.2, б, бывает столь незначительным, что даже в сравнительно большом диапазоне отклонений ∆x1 можно

считать систему линейной. В случае же ярко выраженной нелинейной зависимости линеаризация будет справедлива лишь на соответствующем более узком участке отклонений ∆x1 . Линеаризация может быть совершенно недопустимой при

скачкообразных зависимостях (релейные характеристики, сухое трение). Такого рода зависимости называются существенно нелинейными.

Важно отметить следующее. Если по указанным причинам не может быть подвергнуто линеаризации уравнение только одного звена системы или даже только часть функции F для данного звена, то производят линеаризацию всех остальных нелинейных зависимостей, оставляя только одну или несколько существенно нелинейных.

Второй способ линеаризации. Из приведенной геометрической иллюстрации вытекает другой способ линеаризации уравнений системы автоматического регулирования, который весьма часто применяется на практике. Этот способ заключается в том, что с самого начала все криволинейные зависимости, используемые при составлении уравнений звеньев, заменяются прямолинейными (по касательной в соответствующей точке кривой). Тогда уравнения звеньев сразу будут получаться линейными.

В последующих главах разделов II и III будут использоваться линеаризованные уравнения динамических звеньев. Однако для упрощения записи значок ∆ перед

переменными x1 (t) , x2 (t) , x3 (t) и т. д. будет опускаться в предположении, что эти

переменные представляют собой малые отклонения от некоторого установившегося состояния и линеаризация уравнений уже проделана.

§3.2. О записи линеаризованных уравнений звеньев

Втеории автоматического регулирования в настоящее время принято записывать дифференциальные уравнения звеньев в двух стандартных формах.

Первая форма записи. Дифференциальные уравнения записываются так, чтобы выходная величина и ее производные находились в левой части уравнения, а входная величина и все остальные члены — в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Чтобы привести линеаризованное уравнение (3.5) к такому виду, введем обозначения:

Тогда уравнение (3.5) примет вид

T33∆x3 +T22 ∆x3 +T1∆x3 + ∆x3 = k1∆x1 + k2 ∆x2 + k3 ∆x2 + k4 f1 (t) . (3.9)

В случае, если нелинейная функция F не содержит величины х3, а содержит только ее производные, т. е. если

∂∂F 0 = 0 ,x3

Уравнения (3.9) и (3.10) удобнее записывать в символической форме, введя алгебраизированный оператор дифференцирования p = dtd . Тогда

уравнение (3.9) примет вид

а уравнение (3.10) -

Эти записи надо рассматривать только как сокращенную форму более полных записей (3.9) и (3.10).

Стандартные формы записи уравнений звеньев автоматических систем (3.9) и (3.10) или их сокращенные виды (3.11) и (3.12) можно использовать как для размерных отклонений реальных величин на входе и выходе звена, так и для любых безразмерных относительных отклонений, специально иногда вводимых для упрощения вида уравнений и удобства их исследования. При записи уравнений в стандартной форме коэффициенты k1, k2, k3, k4 называются коэффициентами передачи, а Т1, Т2, Т3 — постоянными времени данного звена.

.

В случае звеньев, у которых выходная и входная величины имеют одинаковую размерность, для коэффициентов передачи используются также следующие термины:

1)коэффициент усиления — для звена, представляющего собой усилитель или имеющего в своем составе усилитель;

2)передаточное число — для редукторов, делителей напряжения, масштабирующих устройств и т. д.