Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975

Как уже говорилось выше, в системах автоматической стабилизации при g(t) = соnst можно при соответствующем выборе начала отсчета получить g(t) = 0, что упрощает выражение (5.5).

При заданных функциях времени в правых частях дифференциальных уравнений (5.2) и (5.5) эти уравнения могут быть решены (проинтегрированы) относительно искомых функций времени, т. е. может быть найдено изменение ошибки регулирования во времени х(t) из (5.2) и движение регулируемого объекта вместе с регулятором у(t) из (5.5). Уравнения (5.1) могут быть также представлены в форме Коши, т. е. в виде совокупности n уравнений первого порядка, где n — порядок полинома D(р):

Здесь xi(i=1, . . ., n), в отличие от (5.1), представляют собой так называемые фазовые координаты системы, fi(i=1, . . ., k)— задающие и возмущающие воздействия, а коэффициенты aij и bij суть вещественные числа.

Если в (5.6) ввести алгебраизированный оператор и обозначить x j = px j , то эта

совокупность уравнений может быть разрешена относительно любой из фазовых координат хi.

§ 5.2. Передаточные функции систем автоматического регулирования

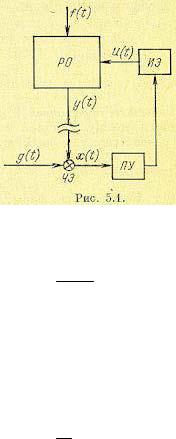
Записанные выше дифференциальные уравнения систем автоматического регулирования (5.2) и (5.5) могут быть получены также на основании понятия передаточной функции, которое было введено в главе 3. Рассмотрим рис. 5.1, где изображена система автоматического регулирования по замкнутому циклу.

Предположим вначале, что чувствительный элемент (ЧЭ) отсоединен от регулируемого объекта (РО), и рассмотрим так называемую разомкнутую систему автоматического регулирования.

Управляющее (или регулирующее) воздействие, которое прикладывает исполнительный элемент (ИЭ) к регулируемому объекту, определяется выражением

u(t) =Wрег ( p)x(t) (5.7)

де х — рассогласование на выходе чувствительного элемента, передаточная функция цепи регулирования.

Регулируемая величина может быть найдена из выражения y(t) =W0 ( p)u(t) −W f ( p) f (t) (5.8)

где W0 ( p) — передаточная функция регулируемого объекта по регулирующему воздействию, Wf ( p) — передаточная функция регулируемого объекта по возмущающему

воздействию f(t).

Как и ранее, предполагается, что на объект регулирования (или на систему регулирования) действует одно возмущающее воздействие f(t). При наличии нескольких возмущений на основании принципа суперпозиции необходимо будет просуммировать члены вида Wk ( p) fk (t) , где Wk ( p) и fk (t) — возмущение и соответствующая ему

передаточная функция по возмущению.

Передаточную функцию, разомкнутой системы можно определить как отношение изображений регулируемой величины и ошибки при нулевых начальных условиях и возмущающих воздействиях, равных нулю:

Y ( p) (5.11)

X ( p)

где р = с +jw — комплексная величина.

Применительно к функциям времени, которые использовались в формулах (5.7) — (5.9), передаточная функция разомкнутой системы дает возможность в символической или операторной форме записать дифференциальное уравнение, связывающее регулируемую величину у(t) с ошибкой х(t) в разомкнутой системе:

y(t) =W ( p)x(t) (5.12)

где p = dtd — алгебраизированный оператор дифференцирования. Учитывая (5.10),

формулу (5.12) можно также записать в виде

Q( p) y(t) = R( p)x(t) (5.13)

Передаточная функция разомкнутой системы имеет весьма большое значение в теории автоматического регулирования, так как многие методы анализа и синтеза основаны на использовании именно этой функции.

Рассмотрим теперь замкнутую систему, т. е. предположим, что чувствительный элемент соединен с регулируемым объектом. При этом можно записать так называемое уравнение замыкания:

x(t) = g(t) − y(t) (5.14)

Решая (5.9) и (5.14) совместно, получаем для регулируемой величины

называется передаточной функцией замкнутой системы или главным оператором. Передаточная функция замкнутой системы дает связь между регулируемой величиной и задающим воздействием при равенстве нулю возмущающих воздействий:

Выражение

называют передаточной функцией замкнутой системы по ошибке. Оно дает связь между ошибкой и задающим воздействием в замкнутой системе при равенстве нулю возмущающих воздействий:

Как и ранее, формулы (5.15), (5.16), (5.18) и (5.20) представляют собой символическую (операторную) запись дифференциальных уравнений. Более строго передаточную функцию замкнутой системы можно определить как отношение изображений регулируемой величины У(р) и управляющего воздействия G(р) при нулевых начальных условиях и отсутствии внешних возмущений:

Ф( p) = GY ((pp)) (5.21)

а передаточную функцию по ошибке — как отношение изображений ошибки X (р) и управляющего воздействия G(р):

=Y ( p)

Фx ( p) G( p) (5.22)

также при нулевых начальных условиях и отсутствии внешних возмущении. Из формул (5.15) и (5.16) видно, что введение автоматического регулирования «уменьшает» отклонение регулируемой величины под действием возмущающих

воздействий в [1 + W(р)] раз по сравнению с отклонением в разомкнутой системе (5.9), когда цепь регулирования разорвана и автоматическое регулирование отсутствует. Передаточная функция разомкнутой системы, может быть представлена в виде дробнорациональной функции от оператора р. В результате сравнения формул (5.2) и (5.16), а также (5.5) и (5.15) видно, что полиномы R(р) и Q(р) в выражении (5.10) совпадают с аналогичными полиномами в дифференциальных уравнениях, приведенных в предыдущем параграфе.

Полином

D( p) = R( p) + Q( p) (5.23)

называется характеристическим.

Приравнивание нулю характеристического полинома дает характеристическое уравнение системы:

D( p) = R( p) +Q( p) = 0 (5.24)

Оно может быть записано в более удобной форме, которая непосредственно получается из

(5.15) или (5.16):

1 +W ( p) = 0 (5.25)

так как характеристическое уравнение системы есть знаменатель операторного, решения, приравненный нулю.

Из рассмотренного видно, что знание передаточной функции разомкнутой системы позволяет найти выражение для ошибки и регулируемой величины в функции задающего и возмущающих воздействий, а также характеристическое уравнение системы. Передаточная функция разомкнутой .системы может находиться непосредственно по структурной схеме и передаточным функциям входящих в нее звеньев (см. ниже, § 5.4) или по какому-либо соотношению, связывающему передаточную функцию разомкнутой системы с другими функциями:

по передаточной функции замкнутой системы (5.17)

по передаточной функции для ошибки (5.19)

Ф( p) = 1−Фx ( p) (5.27) Фx ( p)

по дифференциальному уравнению для ошибки (5.2) или по дифференциальному уравнению для регулируемой величины (5.5)

§ 5.3. Законы регулирования

Под законом регулирования или — в более общем случае — законом управления понимается алгоритм или функциональная зависимость, в соответствии с которыми управляющее устройство формирует управляющее воздействие u(t). Эта зависимость может быть представлена в виде

u(t) = F(x, g, f ) (5.29)

где F — некоторая, в общем случае нелинейная, функция от ошибки х задающего воздействия g и возмущающего воздействия f, а также от их производных и интегралов по времени.

Формула (5.29) обычно может быть записана следующим образом: u(t) = F1 (x) + F2 (g) + F3 ( f ) (5.30)

Первое слагаемое (5.30) соответствует регулированию по отклонению (принцип Ползунова

— Уатта), второе и третье — регулированию по внешнему воздействию (принцип Понселе).

Здесь мы рассмотрим только линейные законы, когда управляющее устройство вырабатывает величину u(t) в функции ошибки в соответствии с линейной формой u(t) = k1 x + k2 ∫xdt + k3 ∫∫xdt 2 +... + k4 x + k5 x +... (5.31)

или в операторной записи

Регулирование по внешнему воздействию будет рассмотрено в § 9.2.

Предположим вначале, что регулируемый объект представляет собой звено статического типа. Это означает, что в установившемся состоянии между регулируемой величиной и управляющим воздействием существует пропорциональная зависимость, вытекающая из (5.8) при равенстве нулю возмущающих воздействий:

yуст = k0uуст

где k0 =W0 (0) — коэффициент передачи объекта.

1. Пропорциональное регулирование. В случае пропорционального регулирования выражение (5.7) для простейшей безынерционной цепи регулирования (см. рис. 5.1) приобретает вид

где А(р) и В(р) — некоторые полиномы от оператора р.

Однако существенным здесь является то обстоятельство, что цепь регулирования представляет собой позиционное (статическое) звено и при p → 0 передаточная функция

Wрег ( p) → k1 , где k1 — коэффициент передачи цепи регулирования.

В связи с изложенным здесь и далее ради облегчения анализа рассматривается упрощенное выражение (5.33), которое является справедливым, по крайней мере, для медленных изменений величины х.

Передаточная функция разомкнутой системы

W ( p) =Wрег ( p)W0 ( p) = k1W0 ( p) .

В установившемся состоянии передаточная функция стремится к значению

limW ( p) = k1k0 = K (5.34}

p→0

Эта величина называется общим коэффициентом усиления разомкнутой системы. Коэффициент усиления является безразмерной величиной, так же как и передаточная функция разомкнутой системы. Это вытекает из соотношения (5.11).

Коэффициент усиления разомкнутой цепи (рис. 5.1) физически представляет (собой отношение установившегося значения регулируемой величины к постоянному значению ошибки х = х0, если цепь регулирования совместно с регулируемым объектом рассматривать как некоторый усилитель, на входе которого действует сигнал в виде ошибки х, а на выходе — усиленный сигнал у. Таким образом, для коэффициента усиления можно записать

K = yуст

x0

Для установившегося состояния замкнутой системы при постоянном задающем воздействии g=g0 формулы (5.16) может быть получено следующее соотношение:

ошибки от возмущающих воздействий в объекте без регулирования.

Таким образом, пропорциональное регулирование позволяет уменьшить установившиеся ошибки в объекте в 1+К раз. Регулирование в этом случае получается статическим, так как при любом конечном значении коэффициента усиления цепи установившаяся ошибка будет отличной от нуля.

Передаточная функция разомкнутой системы (5.10) для этого случая может быть представлена в виде

осуществляется пропорциональная зависимость между скоростью изменения регулирующего воздействия и ошибкой:

dudt = k2 x (5.37)

при этом регулирующее воздействие получается пропорциональным интегралу от ошибки по времени:

u = k2 ∫xdt (5.38)

В операторной форме это можно записать в виде u =Wрег ( p)x = kp2 x (5.39)

Интегральное регулирование может быть осуществлено при помощи каких-либо интегрирующих звеньев, которые были рассмотрены в главе 4.

Аналогично изложенному выше (при рассмотрении пропорционального регулирования) передаточная функция цепи регулирования может иметь более сложный вид, например:

Wрег ( p) = k2 A( p) p B( p)

Однако существенным здесь является то, что цепь регулирования представляет собой или имеет в своем составе интегрирующее звено. Поэтому выражение (5.39) будет справедливым по крайней мере для медленных изменений ошибки х.

Передаточная функция разомкнутой системы регулирования

W ( p) =Wрег ( p)W0 ( p) = kp2 W0 ( p) (5.40)

В установившемся состоянии (р = 0) передаточная функция стремится бесконечности: W ( p) → ∞. В результате первая составляющая ошибки (5.16) при g = g0 = const

обращается в нуль. Вторая составляющая, определяемая наличием возмущающих воздействий, может не обращаться в нуль, так как в установившемся состоянии числитель ее может также стремиться к бесконечности. Поэтому должен быть найден предел выражения при f=f0=const:

который может быть как равным нулю, так и отличным от нуля.

Таким образом, при интегральном регулировании получается система, астатическая по отношению к задающему воздействию. Она может быть при этом как статической, так и астатической по отношению к возмущающим воздействиям.

Передаточная функция разомкнутой системы для случая интегрального регулирования может быть представлена в виде

он представляет собой отношение установившейся скорости изменения регулируемой величины к постоянной по величине ошибке х = х0 = сonst в разомкнутой системе (рис. 5.1):

если цепь регулирования совместно с регулируемым объектом представить себе в виде некоторого усилителя с входной величиной х и выходной у.

Коэффициент Кv, часто называют добротностью по скорости системы регулирования. В дальнейшем, при рассмотрении вопросов точности, будет показано, что он равен отношению постоянной скорости изменения задающего воздействия

dgdt = v = const

к установившейся ошибке:

Kϑ = xv (5.44)

уст

что и определило подобное название.

Регулирование может осуществляться и по второму интегралу от ошибки по времени:

u = k3 ∫∫xdtdt (5.45)

или

отношение установившегося ускорения изменения регулируемой величины к постоянной по величине ошибке х = х0 = const в разомкнутой системе (рис. 5.1):

d 2 2y

Kϑ = dtx0 уст

В этом случае установившееся значение (р = 0) передаточной функции W ( p) → ∞.

Система также будет обладать астатизмом относительно задающего воздействия. Однако это будет уже астатизм второго порядка. Ошибка, определяемая задающим воздействием в (5.16), будет равна нулю не только при g = const, но и при изменении задающего

воздействия с постоянной скоростью dgdt = const .

Аналогичным образом можно получить астатизм третьего и выше порядков, вводя регулирование по третьему и высшим интегралам, т. е. осуществляя регулирование по закону

u =Wрег ( p)x = pkr x (5.49)

где r — порядок астатизма.

Случай пропорционального регулирования (5.30) можно рассматривать как частный случай астатизма при r= 0.

Повышение порядка астатизма приводит к увеличению установившейся точности системы регулирования, но одновременно делает систему более-замедленной в действии, т. е. снижает ее быстродействие, а также приводит к ухудшению устойчивости. Последнее будет показано ниже в главе, посвященной устойчивости.

Для иллюстрации появления замедленности действия систем с интегральным регулированием рассмотрим рис. 5.2. Предположим, что ошибка в системе регулирования начинает возрастать по линейному закону х = аt. В системе пропорционального регулирования по такому же закону начнет создаваться регулирующее воздействие u=k1x=k1at. В системе интегрального регулирования регулирующее воздействие

будет создаваться по закону u = k2 ∫xdt = k2 2at 2

в системе интегрального регулирования не только регулирующее воздействие равно нулю, но равна нулю также и его первая производная, что обусловливает весьма медленный рост u в первые моменты времени. В системе пропорционального регулирования рост u в первые моменты времени происходит более интенсивно, так как наличие ошибки сразу дает появление регулирующего воздействия, в то время как в системе интегрального

регулирования должно пройти некоторое время, пока не «накопится» интеграл ∫xdt .

Рис.

Если перейти к регулированию по второму интегралу, то снижение быстродействия станет еще более заметным.

3. Изодромное регулирование. При изодромном регулировании осуществляется регулирование по пропорциональному и интегральному законам:

В этом случае W ( p) → ∞ при р = 0 и регулирование оказывается астатическим

относительно задающего воздействия. Изодромное регулирование может осуществляться при помощи использования двух параллельных ветвей в цепи регулирования или при помощи установки изодромных звеньев, рассмотренных в главе 4.

Изодромное регулирование сочетает в себе высокую точность интегрального регулирования (астатизм) с большим быстродействием пропорционального регулирования. В первые моменты времени при появлении ошибки система изодромного регулирования работает как система пропорционального регулирования. Это определяется первым слагаемым в правой части закона (5.50). В дальнейшем система начинает работать как система интегрального регулирования, так как с течением времени преобладающее значение начинает приобретать второе слагаемое (5.50).

4. Регулирование по производным. При регулировании по первой производной от ошибки осуществляется зависимость

u = k4 dxdt = k4 px (5.51)

Регулирование по производной не имеет самостоятельного значения, так как в установившемся состоянии производная от ошибки равна нулю и регулирование прекращается. Однако оно может играть весьма большую роль в переходных процессах и вообще в динамике в качестве вспомогательного средства, так как такое регулирование позволяет учитывать не только наличие ошибки, но и тенденцию к росту или уменьшению ошибки. При осуществлении регулирования по закону

u = k1 x + k4 px (5.52)

в системе образуется регулирующее воздействие даже в том случае, когда х = 0, но

dxdt ≠ 0 .Так, например, в рассмотренном выше случае (рис. 5.2) при х = аt регулирующее

воздействие, определяемое вторым слагаемым в правой части (5.52), возникает уже при t=0. В результате введение регулирования по производной от ошибки увеличивает скорость реакции системы регулирования, повышает ее быстродействие, что приводит к снижению ошибок в динамике.

Внекоторых случаях в закон регулирования могут вводиться производные более высоких порядков — вторая, третья и т. д. Это еще больше улучшает динамические качества системы автоматического регулирования. Однако в настоящее время техническая реализация производных выше второго порядка встречает значительные трудности.

Вобщем случае закон регулирования может иметь сложный вид и содержать кроме члена, пропорционального ошибке, также интегралы (для улучшения точности) и производные

(для улучшения динамических свойств) от ошибки. Так, например, часто используется изодромное регулирование с введением первой производной

Таким образом, передаточная функция разомкнутой системы может быть представлена в следующем общем виде:

Для последующего использования при анализе и синтезе передаточную функцию разомкнутой системы удобно представлять в виде произведения сомножителей типа

(1+Тр):

i=1

Если знаменатель или числитель (5.54) содержит комплексные корни то в (5.55) появятся сомножители вида

1 + ap + bp 2 =1 + 2ξTp +T 2 p 2

которые характерны, например, для звеньев колебательного типа.

Формула (5.55) особенно удобна при использовании логарифмических частотных

§ 5.4. Использование структурных схем и графов

Составление основных уравнений системы автоматического регулирования (5.15) и (5.16) во многих случаях может быть значительно облегчено использованием понятия динамических звеньев. Динамические звенья были подробно рассмотрены в главе 4. Часто систему автоматического регулирования можно рассматривать как комбинацию динамических звеньев с определенными типовыми или не типовыми передаточными функциями. Изображение системы регулирования в виде совокупности динамических звеньев с указанием связей между ними носит название структурной схемы. Структурная схема может быть составлена на основе известных уравнений системы, и, наоборот, уравнения системы могут быть получены из структурной схемы. Однако первая задача может иметь различные варианты решения (различные структурные схемы), тогда как вторая задача имеет всегда единственное решение.

Элементы структурных схем приведены в табл. 5.1.

Рассмотрим вначале простейшие сочетания звеньев.

Последовательное соединение звеньев. Такое соединение показано на рис. 5.3. Нетрудно показать, что результирующая передаточная функция равна произведению передаточных функций отдельных звеньев:

Следует подчеркнуть, что это справедливо только в том случае, если соединение выхода предыдущего звена со входом последующего не меняет исходных уравнений каждого звена и, следовательно, его передаточной функции. В подобной последовательной цепи звеньев сигнал проходит только в одном направлении, и она называется детектирующей цепью.

Если при соединении двух звеньев наблюдается влияние одного звена на другое, в результате которого меняются исходные уравнения какого-либо звена, то такое соединение двух звеньев должно рассматриваться новое самостоятельное звено со своей передаточной функцией.

Параллельное соединение звеньев. Такое соединение звеньев изображено на рис. 5.4.

Так как сигналы на выходе всех звеньев складываются, то результирующая передаточная функция равна сумме передаточных функций:

Здесь остаются справедливыми замечания, сделанные выше относительно-взаимного влияния звеньев.