Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975

Термин «коэффициент передачи» можно пояснить следующим образом. Если подать на вход звена только постоянное значение ∆x10 (рис. 3.3, б) и найти установившееся значение выходной величины ∆x30 (рис. 3.3, в), то из (3.9) получим∆x30 = k1∆x10 . Таким

образом, коэффициент k1 показывает отношение выходной величины звена к входной в установившемся режиме.

Следовательно, коэффициент передачи определяет собой наклон (с учетом масштабов по осям) линейной статической характеристики звена (рис. 3.3, а). Заметим, что нелинейную характеристику звена часто называют характеристикой с переменным по входной величине коэффициентом передачи. Из (3.9) очевидно, что

размерностьk1 = размерность выходной ввеличин ∆х3 . размерность входной величины∆х1

В размерность коэффициента передачи может входить также время t. Так, из уравнения (3.9) следует, что

размерностьk3 = размерность ∆х3 × размерность t размерность ∆х2

а из уравнения (3.10) следует, что для такого звена

называются в теории регулирования передаточными функциями. Уравнение (3.13) можно представить в виде

∆x3 =W1 ( p)∆x1 (t) +W2 ( p)∆x2 (t) +W f ( p)∆f1 (t). (3.17)

Выражения (3.13) и (3.17) представляют собой символическую запись дифференциального уравнения (3.9).

Передаточные функции, формулы для которых устанавливаются выражениями (3.14)

— (3.16), вводятся для сокращения записи дифференциальных уравнений и также представляют собой символическую запись дифференциальных уравнений.

Более строго передаточная функция определяется через изображения Лапласа или Карсона — Хевисайда (см. главу 7). Если ввести изображения, например по Лапласу, входных и выходных величин звена:

∆X1 (s) = L[∆x1 (t)], ∆X 2 (s) = L[∆x2 (t)],

∆X 3 (s) = L[∆x3 (t)], F1 (s) = L[f1 (t)],

схемы, показанной на рис. 3.4. Передаточные функции звеньев или отдельных участков схемы позволяют легко получить общее уравнение всей системы в виде (3.13) или (3.20), а в дальнейшем в случае необходимости перейти к исходному дифференциальному уравнению вида (3.9). Подобным же образом могут быть получены передаточные функции и структурные схемы и для других дифференциальных уравнений звеньев, например для рассмотренного выше уравнения (3.10). Подробнее этот вопрос изложен в §

5.4.

ГЛАВА 4 ДИНАМИЧЕСКИЕ ЗВЕНЬЯ И ИХ ХАРАКТЕРИСТИКИ

§ 4.1. Общие понятия

Как уже было сказано, для расчета различных систем автоматического регулирования они обычно разбиваются на динамические звенья. Под динамическим звеном понимают устройство любого физического вида и конструктивного оформления, но описываемое определенным дифференциальным уравнением.

В соответствии с этим классификация звеньев производится именно по виду дифференциального уравнения. Одним и тем же уравнением могут описываться весьма разнообразные устройства (механические, гидравлические, электрические и т. д.). Для теории автоматического регулирования это будет один и тот же тип звена. Конкретные же элементы автоматических систем, их теория, конструкция и расчеты излагаются в соответствующих учебниках и руководствах.

.

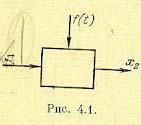
Обозначим входную величину звена через х1 а выходную через х2 (рис. 4.1). Возмущение, действующее на звено, в соответствии с изложенным выше обозначим f(t).

Статическая характеристика любого звена может быть изображена прямой линией (рис. 4.2), так как пока будут рассматриваться линейные или, точнее, линеаризованные системы.

Взвеньях позиционного, или статического, типа линейной зависимостью х2 = kx1 связаны выходная и входная величины в установившемся режиме (рис. 4.2, а). Коэффициент пропорциональности k между выходной и входной величинами представляет собой коэффициент передачи звена.

Взвеньях интегрирующего типа линейной зависимостью - dxdt2 = kx1 связаны

производная выходной величины и входная величина в установившемся режиме (рис. 4.2,6). В этом случае для установившегося режима будет справедливым равенство

x2 = k ∫x1dt , откуда и произошло название этого типа звеньев. Коэффициент

пропорциональности k в этом случае также является коэффициентом передачи звена. Если входная и выходная величины звена имеют одинаковую размерность, то коэффициенту передачи соответствует размерность [сек-1].

В звеньях дифференцирующего типа линейной зависимостью x2 = k dxdt1 связаны в

установившемся режиме выходная величина и производная входной (рис. 4.2, в), откуда и произошло название этого типа звеньев. Коэффициент пропорциональности k; является коэффициентом передачи звена. Если входная и выходная величины имеют одинаковую размерность, то коэффициенту передачи соответствует размерность [сек].

Классификация звеньев, как уже отмечалось, производится по виду дифференциального уравнения или, что тоже, по виду передаточной функции звена. Предположим, что звено, изображенное на рис. 4.1, описывается

дифференциальным уравнением, представленным в стандартной форме:

.

При нулевых начальных условиях, т. е. в том случае, если для t <0 входная и выходная величины, а также их производные тождественно равны нулю, и при отсутствии внешнего возмущения (f(t)=0) может быть найдена передаточная функция звена как отношение изображений по Лапласу (или Карсону) выходной и входной величин:

где k1 — коэффициент передачи звена, T3 =k2/k1 - постоянная времени.

При известной передаточной функции выходная величина (точнее ее изображение по Лапласу или по Карсону) может находиться из выражения

X 2 ( p) =W ( p)X1 ( p).

Аналогичным образом может быть найдена передаточная функция звена по возмущению, если положить при нулевых начальных условиях входное воздействие равным нулю (х= 0). Тогда искомая передаточная функция будет равна отношению изображений выходной величины и внешнего возмущения:

Вдальнейшем изложении для характеристики звена будет использоваться в основном передаточная функция, так как именно она дает связь между входной и выходной величинами, что необходимо знать при использовании того или иного звена в автоматической системе.

Всоответствии с этим в табл. 4.1 приведены передаточные функции десяти разновидностей так называемых типовых динамических звеньев. Под типовым звеном понимается такое звено, которое описывается дифференциальным уравнением не выше второго порядка. Характеристики типовых звеньев рассматриваются более подробно ниже.

Втабл. 4.1 не приводятся сведения о большой группе так называемых корректирующих звеньев, используемых для улучшения динамических качеств автоматических систем. Эти звенья будут рассмотрены в главе 10.

§ 4.2. Временные характеристики

Динамические свойства звена могут быть определены по его переходной функции и функции веса.

Переходная функция, или переходная характеристика, h (t) представляет собой переходный процесс на выходе звена, возникающий при подаче на его вход скачкообразного воздействия при величине скачка, равной единице (рис. 4.3). Такое входное воздействие называется ступенчатой единичной функцией и обозначается x1(t)=1(t), что соответствует х1 = 0 при t<0 и x1=1 при t >0. Предполагается, что единица имеет ту же размерность, что и физическая величина на входе звена.

Если входное воздействие представляет собой неединичную ступенчатую функцию х1=N1(t), выходная величина будет равна х2 = N1 (t).

Более строго переходную функцию можно определить как отношение выходной величины звена х2 (t) к высоте ступенчатого скачка х1 (t) = N1 (t) на его входе, т. е. h (t)= N-1x2(t) . При этом размерность h(t) соответствует размерности передаточной функции звена.

Ступенчатая функция представляет собой распространенный вид входного воздействия в автоматических системах. К такому виду сводятся мгновенное изменение нагрузки электрического генератора, мгновенное возрастание нагрузки на валу двигателя, мгновенный поворот входного валика следящей системы и т. п.

Умножение какой-либо функции времени х (t) на ступенчатую единичную функцию 1 (t) означает, что функция времени х (t) будет существовать только при t>= 0, при t < 0 она обращается в нуль. Это иллюстрируется рис. 4.4.

.

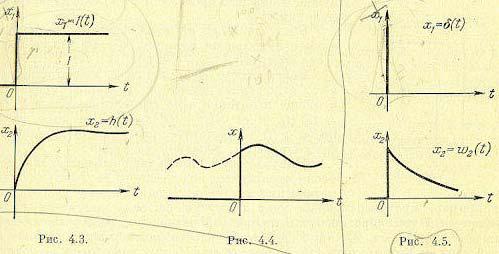Функции веса w(t) представляет собой реакцию звена на единичную импульсную функцию, поданную на его вход рис. 4.5). Единичная импульсная функция, или дельтафункция, представляет собой производную от ступенчатой единичной функции: δ (t) =1'(t) . Дельта-функция тождественно равна нулю повсюду, кроме точки t= 0, где она

стремится к бесконечности.

Основное свойство дельта-функции заключается в том, что

+∞

∫δ(t)dt =1 (4.3)

−∞

т. е. она имеет единичную площадь.

Из последнего выражения следует, что размерность единичной дельта-функции равна [сек-1].

Дельта-функция может быть представлена как предел некоторого выражения, например:

δ(t) = limσ e−σt 1(t)

Нетрудно установить связь между переходной функцией и функцией веса. Рассмотрим входное воздействие звена в виде конечного по высоте и ширине импульса с площадью Nε = 1, прикладываемого при t = 0 (рис. 4.6). Такой импульс может быть заменен двумя ступенчатыми функциями N1 (t) и — N1 (t -ε ), прикладываемыми ко входу звена со сдвигом во времени ε . Тогда выходная величина звена будет равна

x2 (t) = N[h(t) − h(t −ε)] (4.4)

Будем теперь увеличивать высоту импульса N, одновременно уменьшая его ширину ε , но так, чтобы все время площадь импульса равнялась единице,

т. е. Nε = 1. Помножив и поделив правую часть равенства (4.4) на ε и перейдя к пределу, получим. функцию веса

Таким образом, функция веса может быть получена дифференцированием по времени переходной функции.

еде τ — вспомогательное время интегрирования, изменяющееся в пределах от нуля до рассматриваемого текущего момента времени t.

Более подробно методика нахождения переходного процесса при произвольном входном воздействии будет рассмотрена в главе 7.

§ 4.3. Частотная передаточная функция и частотные характеристики

Важнейшей характеристикой динамического звена является его частотная передаточная функция. Для получения ее рассмотрим динамическое звено (рис. 4.1) в случае, когда возмущение f(t) = 0, а на входе имеется гармоническое воздействие х1 =X1Mсоs wt, где Х1M — амплитуда, а w — угловая частота этого воздействия.

На выходе линейного звена в установившемся режиме будет также гармоническая функция той же частоты, но в общем случае сдвинутая по фазе относительно входной величины на уголψ . Таким образом, для выходной величины можно записать

x2 = X 2M cos(wt +ψ ).

Воспользуемся формулой Эйлера и представим входную и выходную величины в виде суммы экспоненциальных функций:

достаточно рассмотреть прохождение только составляющейx1 ' , которая в выходной

Для нахождения соотношения между входной и выходной гармоническими величинами звена воспользуемся его дифференциальным уравнением в виде

дифференциальное уравнение, получим:

T22 (jw)2 X 2M e j(wt +ψ ) +T1 jwX 2M e j(wt+ψ ) + X 2M e j(wt+ψ ) = k1 X1M e jwt + k2 jwX1M e jwt ,

откуда после сокращения на общий множитель e jwt найдем:

Это выражение называется частотной передаточной функцией звена» Таким образом, частотная передаточная функция W(jw) представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной, а аргумент — сдвигу фаз выходной величины по отношению к входной:

modW ( jw) = W ( jw) = X 2M ,

X1M (4.13)

argW ( jw) =ϕ.

В более общей формулировке для входного сигнала любого вида частотную передаточную функцию можно представить как отношение изображений Фурье (частотных изображений) выходной и входной величин:

что непосредственно вытекает из формулы (4.1) при переходе от изображения Лапласа к изображению Фурье; следовательно, частотная передаточная функция легко получается из обычной передаточной функции подстановкой р = jw.

Частотная передаточная функция звена есть изображение Фурье его функции веса, т. е. имеет место интегральное преобразование

W ( jw) = ∞∫w(t)e− jwt dt. (4.15)

0

Частотная передаточная функция может быть представлена в следующем виде:

W ( jw) = A(w)e jψ =U (w) + jV (w), (4.16)

где А (w) — модуль частотной передаточной функции, ψ (w) — аргумент или фаза, U

(w) и V (w) — вещественная и мнимая составляющие частотной; передаточной функции. Модуль частотной передаточной функции находится как отношение модулей числителя и знаменателя. Для рассмотренного выше примера (4.12), аргумент или фаза частотной передаточной функции находится как разность аргументов числителя и

знаменателя. Для (4.12) имеем:

Для нахождения вещественной и мнимой частей частотной передаточной функции необходимо освободиться от мнимости в знаменателе путем умножения числителя и знаменателя на комплексную величину, сопряженную знаменателю, и затем произвести разделение на вещественную и мнимую части. Для (4.12)

Для наглядного представления частотных свойств звена используются так называемые частотные характеристики.

Амплитудно-фазовая частотная характеристика (а. ф. х.) строится на комплексной плоскости. Она представляет собой геометрическое место концов векторов (годограф), соответствующих частотной передаточной функции W ( jw) =U ( jw) + jV (w) при

изменении частоты от нуля до бесконечности (рис. 4.7). По оси абсцисс откладывается вещественная часть U (w) = ReW ( jw) и по оси ординат — мнимая часть V (w) = ImW ( jw) .

Для каждой частоты на комплексной плоскости наносится точка. Полученные точки