Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975

точность вообще не может быть достигнута при современном уровне техники. В цифровых вычислительных машинах принципиально может быть достигнута любая желаемая точность вычислений. Это связано лишь с увеличением числа используемых разрядов в изображении чисел, что вызывает умеренный рост стоимости вычислительных машин при росте их точности.

Цифровые вычислительные машины по своему принципу действия относятся к устройствам дискретного действия. Результаты вычислений выдаются этими машинами не непрерывно, а в виде последовательности дискретных чисел. Цифровые вычислительные машины могут применяться для различных целей. В той числе их можно использовать для решения линейных и нелинейных дифференциальных уравнений с постоянными и переменными коэффициентами, что нужно для исследования процессов в сложных системах управления и регулирования.

Любые вычисления, которые производит цифровая вычислительная машина, сводятся к последовательности арифметических и логических операций. Это означает, что решение дифференциальных уравнений исследуемой системы осуществляется методами численного интегрирования по шагам и точность получаемого решения будет зависеть от величины выбранного шага интегрирования.

Цифровая вычислительная машина имеет в своем составе три основные части (рис. 7.14). Арифметическое устройство предназначается для выполнения операций над числами. Запоминающее устройство осуществляет прием, хранение и выдачу чисел. Управляющее устройство автоматизирует процесс управления машиной в процессе выполнения вычислений.

Число операций, которые может делать машина, ограничено (сложение, вычитание, умножение, деление, перенос числа из одного места памяти в другое и т. п.). Поэтому решение на машине любой задачи должно быть предварительно представлено в виде последовательности таких простейших операций. Отдельные операции выполняются машиной под воздействием управляющих сигналов, которые носят название команд.

Последовательность всех команд, которые заложены в запоминающее устройство машины, образует программу ее работы. Команды вводятся в запоминающее устройство в виде некоторых закодированных чисел.

Программа работы машины составляется с учетом особенностей самой машины (принцип действия, число разрядов, объем памяти и т. п.) и существа используемого численного метода интегрирования дифференциальных уравнений. К численным методам, которые могут быть использованы в цифровых вычислительных машинах, предъявляются некоторые специфические требования. Желательны такие численные методы, которым свойственно циклическое решение задачи, характеризуемое многократным повторением

расчетов по одним и тем же формулам. Это упрощает составление и реализацию программы.

Используемый численный метод должен сводить решение к последовательности простейших арифметических действий. Кроме того, желательно-использовать такой метод, который дает возможность периодического контроля выполненных вычислений.

Как уже отмечалось выше, цифровые вычислительные машины могут дать значительно более высокую точность, чем машины непрерывного действия. Это является их преимуществом. Однако они имеют и недостатки по сравнению с машинами непрерывного действия. К ним относятся: 1) выдача решения не в виде осциллограмм или графиков, а в виде последовательности дискретных чисел, по которым затем необходимо строить графики, 2) трудность программирования задачи, 3) трудность сопряжения вычислительной машины с реальной аппаратурой и 4) во многих случаях большая замедленность в выдаче решения.ы

ГЛАВА 8 ОЦЕНКА КАЧЕСТВА РЕГУЛИРОВАНИЯ

§ 8.1. Общие соображения

Качество работы любой системы регулирования в конечном счете определяется величиной ошибки, равной разности между требуемым и действительным значениями регулируемой величины: х (t) = g (t)—у (t). В системах стабилизации при g (t)=0 ошибка х (t) = — у (t).

Знание мгновенного значения ошибки в течение всего времени работы регулируемого объекта позволяет наиболее полно судить о свойствах системы регулирования. Однако в действительности, вследствие случайности задающего и возмущающего воздействий, такой подход не может быть реализован. Поэтому приходится оценивать качество системы регулирования по некоторым ее свойствам, проявляющимся при различных типовых воздействиях. Для определения качественных показателей системы регулирования в этом случае используются так называемые критерии качества.

В настоящее время разработано большое число различных критериев качества систем регулирования. Все их можно разбить на четыре группы.

Кпервой группе относятся критерии, в той или иной степени использующие для оценки качества величину ошибки в различных типовых режимах. Эту группу назовем критериями точности систем регулирования.

Ко второй группе относятся критерий, определяющие величину запаса устойчивости, т. е. критерии, устанавливающие, насколько далеко от границы устойчивости находится система регулирования.

Почти всегда опасной для системы является колебательная граница устойчивости. Это определяется тем, что стремление повысить общий коэффициент усиления в системе, как правило, приводит к приближению системы именно к колебательной границе устойчивости и затем — к возникновению незатухающих автоколебаний.

Третья группа критериев качества определяет так называемое быстродействие систем регулирования. Под быстродействием понимается быстрота реагирования системы регулирования на появление управляющих и возмущающих воздействий. Наиболее просто быстродействие может оцениваться по времени затухания переходного процесса системы.

Кчетвертой группе критериев качества относятся комплексные критерии, дающие оценку некоторых обобщенных свойств, которые могут учитывать точность, запас устойчивости и быстродействие. Обычно это делается при помощи рассмотрения некоторых интегральных свойств кривой переходного процесса.

При рассмотрении понятий запаса устойчивости и быстродействия можно исходить из двух существующих в настоящее время точек зрения.

Во-первых, можно основываться на характере протекания процессов во времени и использовать для формирования критериев качества переходную или весовую функцию, расположение полюсов и нулей передаточной функции замкнутой системы и т. п.

Во-вторых, можно основываться на некоторых частотных свойствах рассматриваемой системы, характеризующих ее поведение в установившемся режиме при действии на входе гармонического сигнала. К ним относятся полоса пропускания, относительная высота резонансного пика и др.

Оба эти подхода имеют в настоящее время большое распространение и используются параллельно. И тот и другой подход требует изучения условий эксплуатации построенных систем автоматического регулирования, так как только на основании такого изучения можно правильно сформулировать количественные оценки, которые могут быть использованы в практике проектирования и расчета новых систем.

Связь между временными и частотными свойствами системы автоматического регулирования имеет сложный характер и может быть определена в общем виде только в простейших случаях, например для систем, описываемых дифференциальным уравнением второго порядка.

Однако отсутствие зависимостей, связывающих в общей форме свойства системы во временном и частотном представлениях, не может служить препятствием для развития и независимого использования критериев качества того или иного направления.

Использование того или иного подхода при формулировании критериев качества определяется в настоящее время удобствами его применения в системах конкретного вида, а также, в известной мере, сложившимися в данной области традициями.

§ 8.2. Точность в типовых режимах

Для оценки точности системы регулирования используется величина ошибки в различных типовых режимах. Ниже будут рассмотрены наиболее употребительные режимы.

1. Неподвижное состояние. В качестве типового режима рассматривается установившееся состояние при постоянных значениях задающего и возмущающего воздействий. Ошибка системы в этом случае называется статической Величина ошибки можёт бытъ найдена из общего выражения (5.2). Для этого необходимо положить g (t) = g0 — const. Далее необходимо учесть действующие на систему возмущения. В общем случае их может быть несколько: f1(t), f2(t) и т. д. Тогда в правой части (5.2) появится несколько слагаемых, определяемых имеющимися возмущениями. В неподвижном состоянии необходимо положить f1(t) = f10 = const,

f2(t) = f20 = const и т. д. Затем можно использовать изображения функций по Лапласу или Карсону

— Хевисайду. Используем, например, изображения Карсона — Хевисайда. Тогда изображение

постоянной величины равно ей самой, т. е. 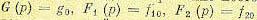Далее необходимо воспользоваться теоремой предельного перехода и получить установившееся значение ошибки (статическую ошибку):

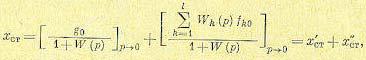(8.1)

где l — число действующих на систему возмущений, а Wk (р) = - Wf(р).

Это же выражение может быть получено из операторного уравнения (5.16), если

оператор дифференцирования положить равным нулю.

Первое слагаемое (8.1) представляет cобой составляющую статической ошибки, определяемую задающим воздействием. Эта составдяюшдя, в соответствии с изложенным в § 5.3, может быть отличной от нудя только в следящих системах при статическом регулировании.

В статических системах W(0) = К представляет собой общий коэффициент усиления по разомкнутой цепи. В этом случае первое слагаемое (8.1) может быть представлено в виде

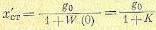(8.2)

Однако эта составляющая ошибки практически всегда может быть сведена к нулю посредством использования неединичной обратной связи или путем масштабирования задающего воздействия или регулируемой величины (см. § 9.3).

При астатическом регулировании W(0) → ∞. Поэтому первая составляющая (8.1) обращается в нуль.

В системах стабилизации g(t) = 0, что также обращает в нуль х'ст. В связи с этим практически во всех случаях первая составляющая статической ошибки может быть принята равной нулю.

Второе слагаемое (8.1) никогда не обращается в нуль, так как даже использование регулирования с астатизмом высокого порядка и использование принципа регулирования по возмущению (см. § 9.2) могут обратить в нуль лишь часть слагаемых, находящихся под знаком суммы (8.1).

При выводе выражения (8.1) предполагалось, что чувствительный элемент, определяющий разность между требуемым и действительным значениями регулируемой величины, является идеальным и определяет имеющуюся ошибку в соответствии с выражением х(t) = g(t)-у(t). В действительности чувствительному элементу как измерительному органу присущи свои ошибки.

Ошибку чувствительного элемента можно рассматривать также как некоторое возмущающее воздействие и считать, что она входит во второе слагаемое (8.1). Однако на практике удобнее эту ошибку учитывать отдельно и считать, что статическая ошибка равна (при х'ст = 0)

,

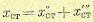где x’’ст представляет собой второе слагаемое в выражении (8.1) и определяется внешними возмущениями, х'’’ст является ошибкой чувствительного элемента.

Рассмотрим теперь ошибку регулирования х”ст. Примем для простоты, что на систему действует одно возмущающее воздействие f1. Тогда в статической системе получим

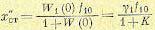(8.4)

Вэтом равенстве γ1 представдяетсдставляет собой – отношение установившейся ошибки

кпостоянному возмущению (коэффициент статизма) в системе с разомкнутой цепью регулирования. Эта же самая величина, деленная на 1+К, соответствует коэффициенту статизма в замкнутой системе регулирования.

Величина 1 + К, по сути дела, показывает эффективность регулирования с точки зрения уменьшения установившейся ошибки.

Вастатической системе W(0)→∞. Однако это еще не означает, что х'’ст= 0, так как возможен случай, когда W1(0)→-∞. Вследствие этого для каждого действующего на систему возмущения необходимо определить факт наличия или отсутствия установившейся ошибки посредством нахождения значения (8.4).

Для иллюстрации этого на рис. 8.1 изображена структурная схема системы автоматического регулирования. Она содержит объект с передаточной функцией W0(р) и астатический регулятор с

передаточной функцией 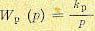. Пусть объект не имеет интегрирующих свойств

.

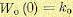На систему действуют два возмущения — f1 u f2. В разомкнутой системе (как показано на рис. 8.1)

и в замкнутой

Таким образом, первое возмущение дает статическую ошибку, а второе не дает. Из рассмотрения рис. 8.1 видно, что возмущение f1 приложено до интегрирующего звена, f2—после. Из этого и вытекает правило, по которому можно определить, устраняет ли астатический закон регулирования статическую ошибку от какого-либо возмущения. Для выполнения этого необходимо, чтобы интегрирующий элемент был включен в цепь регулирования до места приложения данного возмущения. Это объясняет, в частности, тот факт, что включение интегрирующих элементов и повышение степени астатизма не дает возможности устранить ошибку чувствительного элемента хуст, которую можно рассматривать как возмущение.

2. Движение с постоянной скоростью. В качестве второго типового режима используется режим движения системы с постоянной скоростью V=const, который будет наблюдаться в установившемся состоянии при задающем воздействии, изменяющемся по закону g(t)=V, где V = const, и при постоянных значениях возмущающих воздействий f1(t)= f10, f2(t)=f20 и т. д. Этот режим имеет смысл только в следящих системах и системах программного регулирования.

Используя изображения Карсона — Хевисайда, в этом случае получаем:

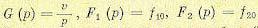и т.д.

Из общего выражения для ошибки (5.16) посредством теоремы о предельном переходе монсет быть найдена установившаяся ошибка в этом режиме:

(8.5)

Второе слагаемое этого выражения дает статическую ошибку (при условии, что возмущающие воздействия такие же, как в неподвижном положении системы), в которой может быть также учтена ошибка чувствительного элемента.

Первое слагаемое (8.5) имеет смысл только при астатизме первого порядка, т. е. в том случае, когда передаточная: функция разомкнутой системы может быть представлена в виде

(5.42)

Тогда выражение (8.5) приводится к виду

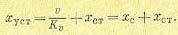(8.6)

Таким образом, в этом типовом режиме установившаяся ошибка будет слагаться из статической ошибки и добавочной скоростной ошибки, равной отношению скорости задания к добротности системы по скорости:

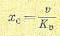(8.7)

Так как система может двигаться с различными скоростями, то качество ее удобнее характеризовать не самой скоростной ошибкой, которая является переменной величиной, а значением добротности по скорости

(8.8)

В статических системах первое слагаемое (8.6) стремится к бесконечности; при астатизме выше первого порядка это слагаемое стремится к нулю. Поэтому режим движения с постоянной скоростью используется для оценки точности только систем с астатизмом первого порядка, главным образом следящих систем для которых такой режим является характерным.

3. Движение с постоянным ускорением. В качестве третьего типового режима используется режим установившегося движения системы регулирования с постоянным ускорением ε=const;. В

этом случае задающее воздействие меняется по закону 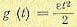. Возмущающие воздействия принимаются постоянными, как и во втором типовом режиме. Этот режим имеет смысл только в следящих системах и системах программного регулирования. Аналогично изложенному выше, установившееся значение ошибки в этом режиме может быть найдено из выражения

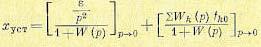(8.9)

Второе слагаемое (8.9), как и ранее, дает статическую ошибку. Первое слагаемое (8.9) имеет смысл только при астатизме второго порядка, когда передаточная функция разомкнутой системы может быть представлена в виде

Тогда выражение (8.9) приводится к виду

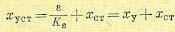(8.10)

Первое слагаемое (8.10) представляет собой Добавочную ошибку от постоянного ускорения. Как и в предыдущем случае, качество системы может быть оценено величиной добротности по ускорению

(8.11)

Этот типовой режим используется только для систем регулирования с астатизмом второго порядка, главным образом следящих систем.

4. Движение по гармоническому (синусоидальному) закону. Такой режим используется весьма часто, так как он позволяет наиболее полно оценить динамические свойства системы регулирования. Задающее воздействие принимается изменяющимся по закону

В зависимости от конкретного вида системы регулирования возмущающие воздействия в рассматриваемом режиме могут оставаться постоянными или меняться.

Случай постоянства возмущающих воздействий приводит, как и в рассмотренных выше втором и третьем типовых режимах, к появлению некоторой постоянной ошибки xст.

Более вероятным является случай, когда возмущающие воздействия при движении системы в этом режиме меняются во времени. Это объясняется тем, что при движении по гармоническому закону непрерывно будет меняться направление движения системы, а следовательно, одновременно будет меняться направление действующих в системе сил сухого трения. Этот случай является довольно сложным, и он может рассматриваться только в приложении к конкретным системам регулирования. Рассмотрим ошибку, определяемую только первым слагаемым выражения (5.16):

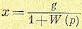(8.13)

В линеаризованной системе при гармоническом задающем воздействии (8.12) ошибка в установившемся режиме будет также меняться по гармоническому закону с частотой ωk:

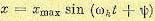(8.14)

Точность системы в этом режиме может быть оценена по амплитуде ошибки, которая может быть найдена из (8.13) на основании символического метода подстановкой :

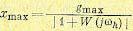(8.15)

Так как предполагается, что амплитуда ошибки значительно меньше амплитуды входного воздействия: то, следовательно, модуль знаменателя (8.15), значительно больше единицы. Это позволяет с большой точностью выражение (8.15) заменить приближенным

где A(ωk) — модуль частотной передаточной функции разомкнутой системы при ω=ωk.

Последняя формула позволяет легко вычислять амплитуду ошибки в установившемся режиме. Для этого необходимо располагать либо аналитическим выражением для передаточной функции разомкнутой системы, либо иметь экспериментально снятую амплитудную или амплитудно-фазовую частотную характеристику разомкнутой системы.

Формула (8.16) широко используется также при расчете системы методом логарифмических амплитудных частотных характеристик (л.а.х.). В этом случае модуль A(ωk) в децибелах, т. е. L(ωk) = 20lg A(ωk), равен ординате л.а.х. при частоте ω=ωk (рис. 8.2, а).

Простота выражения (8.16) позволяет легко решить обратную задачу, т. е. сформулировать требования к л.а.х., которые необходимо выполнить, чтобы амплитуда ошибки в установившемся режиме была не больше заданной. Для этого необходимо по заданному значению амплитуды задающего воздействия gmax и допустимой амплитуде ошибки xmax вычислить требуемое значение модуля частотной передаточной функции разомкнутой системы в децибелах:

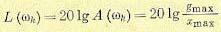(8.17)

Это значение модуля необходимо отложить на логарифмической сетке яри частоте управляющего воздействия ω=ωk. Полученная точка Аk (рис. 8.2, б) обычно называется контрольной точкой для л.а.х. Для того чтобы амплитуда ошибки в системе не превосходила допустимого значения xmax, л.а.х. должна проходить не ниже контрольной точки Аk. Если л.а.х. пройдет через эту точку, то амплитуда ошибки будет как раз равна допустимому значению. Если л.а.х. пройдет ниже точки Аk, то ошибка будет больше допустимого значения.

§ 8.3. Коэффициенты ошибок

Рассматриваемый метод может применяться как для задающего g(t), так и для возмущающего / (г) воздействий. Не снижая общности рассуждений, рассмотрим случай, когда имеется только задающее воздействие.

Если функция времени § (2) имеет произвольную форму, но достаточно плавную вдали от начальной точки процесса в том смысле, что через некоторое время существенное значение имеет только конечное число m производных

то ошибку системы можно определить следующим образом. Из формулы (5.20) можно найти изображение ошибки

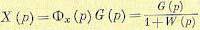(8.18)

где Фх (р) — передаточная функция замкнутой системы по ошибке, G (р) — изображение задающего воздействия.

Разложим передаточную функцию по ошибке в выражении (8.18) в ряд ло возрастающим степеням комплексной величины р:

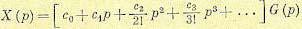(8.19)

сходящийся при малых значениях р, т. е. при достаточно больших значениях времени t, что соответствует установившемуся процессу изменения регулируемой величины при заданной форме управляющего воздействия. Переходя в выражении (8.19) к оригиналу, получаем формулу для установившейся ошибки

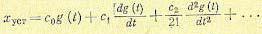(8.20)

Величины c0, c1, c2 ... называются коэффициентами ошибок. Они могут определяться согласно общему правилу разложения функции в ряд Тейлора по формулам

Так как передаточная функция по ошибке представляет собой дробно-рациональную функцию, то коэффициенты ошибок можно более просто получить делением числителя на знаменатель и сравнением получающегося ряда с выражением (8.19).

Коэффициент с0 может быть отличным от нуля только в статических системах и то только в тех случаях, когда не принимаются меры по устранению первой составляющей статической ошибки посредством масштабирования или использования неединичных обратных связей (см. § 9.3).

В системах с астатизмом первого порядка с0 = 0, а коэффициент с4 связан с добротностью по скорости соотношением

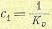(8.21)

В системах с астатизмом второго порядка с0 = 0 и с1 = 0,

а коэффициент с2 связан с добротностью по ускорению соотношением

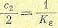(8.22)

При исследовании ошибки от возмущающего воздействия можно получить все коэффициенты не равными нулю при астатизме любого порядка, так как астатизму по задающему воздействию может соответствовать наличие статической ошибки по возмущению.

Если задающее воздействие g (t) имеет ограниченное число производных, то ряд (8.20) будет иметь ограниченное число членов. Предположение, что коэффициенты ошибок представляют-собой постоянные числа, обусловливает применение этого метода для сравнительно медленно меняющихся входных воздействий g(t) или f(t), когда можно пренебречь влиянием переходной составляющей процесса и рассматривать только вынужденное движение системы.

Пример. Определим первые три коэффициента ошибки по задающему воздействию, если передаточная функция разомкнутой системы имеет вид

Передаточная функция по ошибке 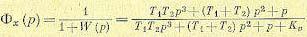Деля числитель на знаменатель, получаем ряд

Сравнение этого ряда с (8.19) дает

Так, например, если задающее воздействие в этой системе меняется по закону

то установившаяся ошибка будет

§ 8.4. Определение запаса устойчивости и быстродействия по переходной характеристике

Оценку запаса устойчивости и быстродействия можно произвести по виду кривой переходного процесса в системе автоматического регулирования прж некотором типовом входном воздействии, которым может быть как задающее, так и возмущающее воздействие. В качестве типового входного воздействия рассматривается обычно единичный скачок. В этом случае кривая переходного процесса для регулируемой величины будет представлять собой переходную характеристику системы (рис. 8.3). Она может строиться для регулируемой величины у (t) или для ошибки х (t).

Склонность системы к колебаниям, а следовательно, и запас-устойчивости могут быть охарактеризованы максимальным значением регулируемой величины г/тах или так называемым перерегулированием

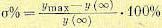где у (∞) ≠ 0 представляет собой установившееся значение регулируемой величины после завершения переходного процесса.

Допустимое значение перерегулирования для той или иной системы автоматического регулирования может быть установлено на основании опыта эксплуатации подобных систем. В большинстве случаев считается, что запас устойчивости является достаточным, если величина перерегулирования не превышает 10-30%. Однако в некоторых случаях требуется, чтобы переходный процесс протекал вообще без перерегулирования, т. е. был монотонным; в ряде других случаев может допускаться перерегулирование 50-70%.

Быстродействие системы может определяться по длительности переходного процесса tп. Длительность переходного процесса определяется как время, протекающее от момента приложения на вход единичного скачка до момента, после которого имеет место неравенство

(8.24}

где ∆ — заданная малая постоянная величина, представляющая собой обычно допустимую ошибку. Величина у (∞) в частном случае может равняться нулю.

Допустимое значение времени переходного процесса определяется на основании опыта эксплуатации систем регулирования. В следящих системах в качестве единичного скачка принимается мгновенное изменение управляющего воздействия g(t) = 1(t). В этом случае под величиной ∆ обычно понимают некоторую долю входного воздействия, составляющую, как правило, от 1 до 5% величины скачка на входе.

Иногда дополнительно к величине перерегулирования σ% (или к величине ymax) задается допустимое число колебаний, которое может наблюдаться в течение времени переходного процесса. Это число составляет обычно 1-2. В некоторых системах колебания могут вообще не допускаться, а иногда может допускаться до 3-4 колебаний.