
Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975
.pdf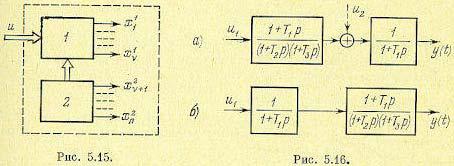
§ 5.6. Управляемость и наблюдаемость
Рассмотрим n-мерное пространство состояния X, в котором каждому состоянию системы соответствует некоторое положение изображающей точки, определяемое значениями фазовых координат xi (i = 1, . . ., n).
Пусть в пространстве состояния X заданы два множества  и
и 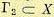 . Рассматриваемая система будет управляемой, если существует такое управление
. Рассматриваемая система будет управляемой, если существует такое управление
 , определенное на конечном интервале времени
, определенное на конечном интервале времени 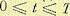 , которое переводит изображающую точку в пространстве X из подобласти Г1 в подобласть Г2.
, которое переводит изображающую точку в пространстве X из подобласти Г1 в подобласть Г2.
Можно сузить определение управляемости и понимать под ней возможность перевода изображающей точки из любой области пространства состояния X в начало координат. Система будет полностью управляемой, если каждое состояние управляемо в этом смысле.
От пространства состояния X перейдем к другому пространству 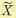 посредством неособого преобразования
посредством неособого преобразования  , причем
, причем 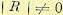 , где R — матрица коэффициентов n x n.
, где R — матрица коэффициентов n x n.
Тогда вместо (5.87) будем иметь
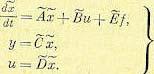 (5.91)
(5.91)
Здесь использованы преобразованные матрицы коэффициентов: 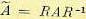 ,
,
 ,
,  .
.
Введение новых фазовых координат посредством неособого преобразования
 приводит к эквивалентным системам различной структуры.
приводит к эквивалентным системам различной структуры.
При некотором преобразовании может оказаться, что часть управляющих величин не входит в некоторые дифференциальные уравнения (5.91) или часть фазовых координат не участвует в формировании выхода у. В первом случае система будет не полностью управляемой, а во втором — не полностью наблюдаемой.
В случае не полностью управляемой системы ее исходные уравнения (5.87) могут быть представлены в виде
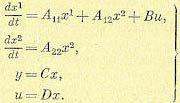 (5.92)
(5.92)
Ох.
Это иллюстрирует рис. 5.15. Набор фазовых координат х1 соответствует управляемой части фазовых координат, а набор ж2 — неуправляемой части.
Р. Калманом [50] был доказан критерий управляемости, который гласит, что размерность V управляемой части системы, то есть порядок первой группы уравнений (5.91), совпадает с рангом матрицы
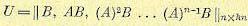 (5.93)
(5.93)
При v = n система полностью управляема, при 0 < v < n не полностью управляема и при v = 0 полностью неуправляема.
На рис. 5.16, а изображен простейший пример. Если рассматривать выходную величину у (t) при ненулевых начальных условиях, то можно записать
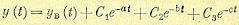 (5.94)
(5.94)
где 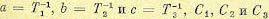 определяются начальными условиями до приложения входного сигнала u1 (t), а ув (t) — вынужденная составляющая. Система устойчива при а>0, b>0 и с>0.
определяются начальными условиями до приложения входного сигнала u1 (t), а ув (t) — вынужденная составляющая. Система устойчива при а>0, b>0 и с>0.
Если начальные условия до приложения u1 (t) были нулевыми, то поведение системы может быть рассчитано по передаточной функции
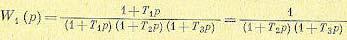 (5.95)
(5.95)
В этом случае по интегралу Дюамеля — Карсона
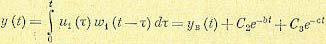 (5.96)
(5.96)
Как следует из выражений (5.95) и (5.96), система во втором случае-описывается дифференциальным уравнением не третьего, а второго порядка. Система будет устойчивой даже при а. < 0.
Рассмотренная система будет не полностью управляемой. В ней оказывается, что n = 3, а v = 2.
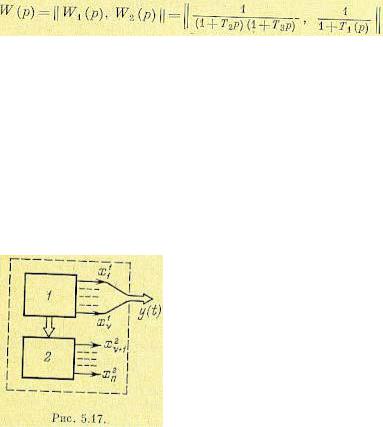
При введении второй составляющей управления u2 (t) система оказывается полностью управляемой, и ей будет соответствовать матрица-строка передаточных функций по управлению
В случае не полностью наблюдаемой системы ее уравнения могут быть, представлены в виде
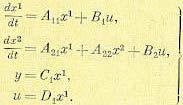 (5.97),
(5.97),
Эти уравнения отличаются от (5.87) тем, что фазовые координаты группы x2 не входят ни в выражения для у и u, ни в первое уравнение, куда входят только фазовые координаты группы x1. Группа фазовых координат x2 относится к ненаблюдаемым. Это иллюстрирует рис. 5.17.
Р. Калманом [50] показано, что порядок первой группы уравнений v совпадает с рангом: матрицы
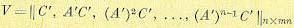 (5.98)
(5.98)
При v = n система полностью наблюдаема, при 0 < v <n — не полностью наблюдаема ж при v = 0 полностью ненаблюдаема.
На рис. 5.16, б изображен простейший пример. Для него легко показать, что в формировании выхода участвуют только две фазовые координаты из трех.
В общем случае система может содержать четыре группы фазовых координат: управляемую, но ненаблюдаемую часть x1, управляемую и наблюдаемую часть x2, неуправляемую и ненаблюдаемую часть x3 и неуправляемую, но наблюдаемую часть x4.
Исходные уравнения системы (5.87) в этом случае можно для самого, общего случая записать следующим образом:
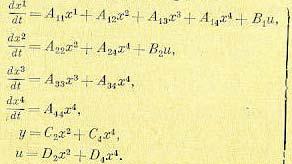 (5.99)
(5.99)
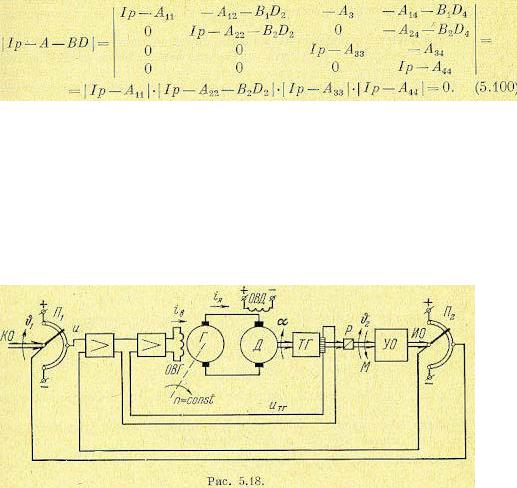
Левая часть характеристического уравнения системы в этом случае содержит четыре сомножителя:
Управляемость и наблюдаемость системы в изложенном смысле не всегда совпадает с практическими представлениями. Даже если какая-либо фазовая координата и может быть вычислена по доступным для измерения выходным величинам, обработка измеренных величин может быть, во-первых, сложной и, во-вторых, она может быть затруднена наличием помех. Поэтому практически наблюдаемыми координатами обычно считаются те из них, которые могут быть непосредственно измерены датчиками различных типов.
§ 5.7. Уравнения следящей системы
Рассмотрим следящую систему, принципиальная схема которой изображена на рис. 5.18. Задающим устройством является командная ось КО, вращаемая извне по
произвольному закону 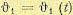 . Этот угол должен повторяться на управляемом объекте УО, ось которого является исполнительной осью ИО. Мощность, требуемая для вращения командной оси ничтожна, так как с командной осью сцеплен только движок потенциометра П1. Мощность, которую может потреблять для своего вращения управляемый" объект, значительно выше и обеспечивается установкой двигателя Д соответствующей номинальной мощности. В этом, а также в дистанционности управления заключается смысл использования подобной следящей системы воспроизведения угла поворота.
. Этот угол должен повторяться на управляемом объекте УО, ось которого является исполнительной осью ИО. Мощность, требуемая для вращения командной оси ничтожна, так как с командной осью сцеплен только движок потенциометра П1. Мощность, которую может потреблять для своего вращения управляемый" объект, значительно выше и обеспечивается установкой двигателя Д соответствующей номинальной мощности. В этом, а также в дистанционности управления заключается смысл использования подобной следящей системы воспроизведения угла поворота.
Сравнение углов поворота командной и исполнительной осей осуществляется при помощи двух потенциометров П1 и П2. Если углы поворота командной и исполнительной осей не равны, 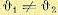 , то возникает напряжение рассогласования u, которое поступает на вход первого электронного усилителя. Далее усиленный сигнал после прохождения через два электронных усилителя подводится к обмотке возбуждения генератора ОВГ, привод, которого не показан на схеме. Якорь генератора Г соединен с якорем двигателя Д, обмотка которого (ОВД) подключена к постоянному напряжению. 128
, то возникает напряжение рассогласования u, которое поступает на вход первого электронного усилителя. Далее усиленный сигнал после прохождения через два электронных усилителя подводится к обмотке возбуждения генератора ОВГ, привод, которого не показан на схеме. Якорь генератора Г соединен с якорем двигателя Д, обмотка которого (ОВД) подключена к постоянному напряжению. 128
В результате при появлении рассогласования 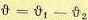 двигатель начинает вращаться в сторону уменьшения ошибки до согласования двух осей. Задающим воздействием здесь является угол поворота
двигатель начинает вращаться в сторону уменьшения ошибки до согласования двух осей. Задающим воздействием здесь является угол поворота  . В качестве возмущающего воздействия рассмотрим момент нагрузки М (t) на оси управляемого объекта.
. В качестве возмущающего воздействия рассмотрим момент нагрузки М (t) на оси управляемого объекта.
Для улучшения динамических качеств следящей системы в ней предусмотрена отрицательная обратная связь по напряжению тахогенератора (ТГ).
Будем считать, что все звенья системы линейны, за исключением электромашинного усилителя (генератора), у которого электродвижущая сила е связана с током возбуждения 1В нелинейной кривой намагничивания генератора. Однако и здесь при сравнительно небольших напряжениях якоря (примерно до половины номинального) можно зависимость между е и iв считать также линейной.
Таким образом, в рассматриваемой системе отпадает необходимость линеаризации и можно сразу приступить к составлению уравнений. Для этой цели разобьем систему на динамические звенья и найдем их передаточные функции.
Чувствительный элемент. Напряжение на выходе первого потенциометра будет
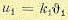 и на выходе второго
и на выходе второго 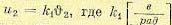 - крутизна, или коэффициент передачи потенциометра. Напряжение на выходе чувствительного
- крутизна, или коэффициент передачи потенциометра. Напряжение на выходе чувствительного
элемента равно разности
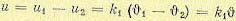 (5.101)
(5.101)
Это дает передаточную функцию чувствительного элемента
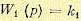 (5.102)
(5.102)
Электронные усилители. Считая усилители безынерционными, можно записать их передаточные функции в виде
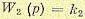 (5.103)
(5.103)
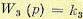 (5.104)
(5.104)
где k2 и k3 — коэффициенты усиления по напряжению первого и второго усилителей. Обмотка возбуждения генератора. Дифференциальное уравнение можно записать на
основе второго закона Кирхгофа:
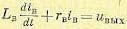 (5.105)
(5.105)
где rв и Lв — суммарные сопротивление и индуктивность цепи возбуждения с учетом выходного каскада усилителя.
Приведем это уравнение к стандартному виду:
 (5.106)
(5.106)
где 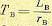 — постоянная времени цепи возбуждения.
— постоянная времени цепи возбуждения.
Отсюда находим передаточную функцию обмотки возбуждения:
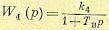 (5.107)
(5.107)
Генератор. Для прямолинейной части характеристики намагничивания можно положить
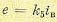 (5.108)
(5.108)
где k5 — коэффициент пропорциональности между э.д.с. генератора и током возбуждения в линейной части характеристики. Отсюда получаем передаточ- , ную функцию генератора:
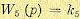 (5.109)
(5.109)
Двигатель. Так как при фиксированном возбуждении двигатель имеет две степени свободы, то необходимо иметь для него два исходных дифференциальных уравнения. Первое уравнение может быть получено, если записать второй закон Кирхгофа для цепи якоря:
 (5.110)
(5.110)
Второе уравнение представляет собой закон равновесия моментов на валу двигателя:
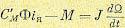 (5.111)
(5.111)
В этих уравнениях Lя и rя — индуктивность и сопротивление цепи якоря
(суммарные), 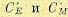 — коэффициенты пропорциональности, J — приведенный к оси двигателя суммарный момент инерции,
— коэффициенты пропорциональности, J — приведенный к оси двигателя суммарный момент инерции,  — угловая скорость двигателя, Ф — поток возбуждения, М — момент нагрузки, приведенный к валу двигателя.
— угловая скорость двигателя, Ф — поток возбуждения, М — момент нагрузки, приведенный к валу двигателя.
Так как поток возбуждения двигателя Ф = const, то можно положить
 .
.
Вводя оператор дифференцирования и решая уравнения (5.110) и (5.111) совместно, получаем
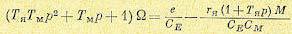 (5.112)
(5.112)
Здесь введены две постоянные времени двигателя: электромеханическая постоянная времени
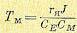 (5.113)
(5.113)
и постоянная времени якорной цепи
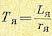 (5.114)
(5.114)
Коэффициенты пропорциональности СЕ и СМ могут быть найдены из соотношений
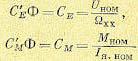 (5.114)
(5.114)
где Uном и Iяном — номинальные значения напряжения и якорного тока двигателя,
MНОМ и 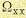 — номинальный вращающий момент и скорость идеального холостого хода двигателя.
— номинальный вращающий момент и скорость идеального холостого хода двигателя.
Учитывая эти соотношения, электромеханическую постоянную времени можно представить в другом виде:
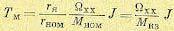 (5.115)
(5.115)
где 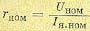 — номинальное сопротивление якоря двигателя, Мкз - момент короткого замыкания двигателя (вращающий момент заторможенного двигателя).
— номинальное сопротивление якоря двигателя, Мкз - момент короткого замыкания двигателя (вращающий момент заторможенного двигателя).
В формуле (5.155) перейдем к углу поворота двигателя а, который связан с угловой скоростью 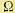 зависимостью
зависимостью  .
.
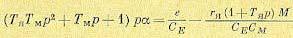 (5.116)
(5.116)
Из последнего выражения, сравнивая его с формулой (5.9), можно получить передаточную функцию двигателя, связывающую его угол поворота а с э. д. с. генератора:
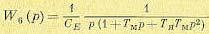 (5.117)
(5.117)
и передаточную функцию по возмущению, связывающую угол поворота а с моментом M, приложенным к его оси:
 (5.118)
(5.118)
Редуктор. Считая редуктор линейным безынерционным звеном, запишем его передаточную функцию в виде
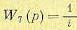 (5.119)
(5.119)
где i > 1 — передаточное отношение редуктора.
Тахогенератор. Передаточная функция тахогенератора, в соответствии с § 4.7, еоответствует идеальному дифференцирующему звену:
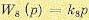 (5.120)
(5.120)
где ks — коэффициент пропорциональности между э.д.с. генератора и ско- \ ростью его вращения.
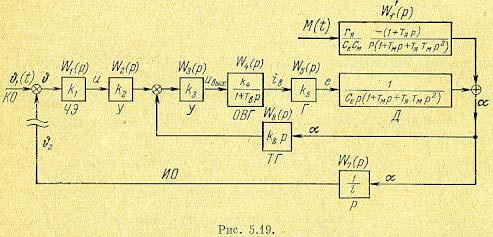
Все звенья рассматриваемой системы, кроме тахогенератора, включены последовательно. Это отображено на структурной схеме рис, 5.19. Тахо-генератор включен в цепь местной обратной связи.
Размыкая главную цепь системы, как показано на рис. 5.16 (так, чтобы не нарушать включения местной обратной связи), получаем передаточную функцию разомкнутой системы
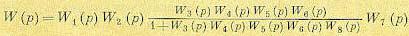 (5.121)
(5.121)
После подстановки выражений для передаточных функций звеньев получаем
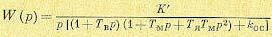 (5.121)
(5.121)
Здесь введен общий коэффициент усиления цепи регулирования без учета действия местной обратной связи

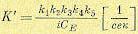 (5.123)
(5.123)
и коэффициент усиления по цепи местной обратной связи
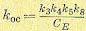 (5.124)
(5.124)
Выражение (5.122) можно переписать в ином виде:
 (5.125)
(5.125)
где
 (5.126)
(5.126)
Результирующий коэффициент усиления основной цепи с учетом действия местной обратной связи, называемый также добротностью по скорости, будет
Найдем операторные выражения для регулируемой величины 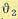 и ошибки
и ошибки 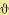 по общим формулам (5.15) и (5.16). Для этого необходимо найти передаточную функцию по
по общим формулам (5.15) и (5.16). Для этого необходимо найти передаточную функцию по
возмущению Wf (р), связывающую угол поворота 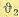 с возмущением М при разомкнутой главной цепи, но замкнутой цепи местной обратной связи. Из структурной схемы (рис. 5.19) при разомкнутой главной обратной связи и при разомкнутой местной обратной связи будет
с возмущением М при разомкнутой главной цепи, но замкнутой цепи местной обратной связи. Из структурной схемы (рис. 5.19) при разомкнутой главной обратной связи и при разомкнутой местной обратной связи будет
 (5.128)
(5.128)
где i — передаточное отношение редуктора.
При замыкании местной обратной связи в соответствии с формулой (5.59) получаем
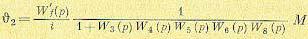 (5.129)
(5.129)
откуда искомая передаточная функция по возмущению
где kос, а, b и с определяются формулами (5.124) и (5.126). 132
Имея теперь значения передаточных функций 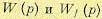 , по общим формулам (5.15) и (5.16) находим операторное выражение для регулируемой величины
, по общим формулам (5.15) и (5.16) находим операторное выражение для регулируемой величины
Из (5.132) можно, в частности, получить установившуюся ошибку в неподвижном
положении при 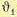 (t) = const и М (t) = М0 = const. Для этого необходимо в (5.175) положить р = 0:
(t) = const и М (t) = М0 = const. Для этого необходимо в (5.175) положить р = 0:
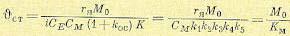 (5.133)
(5.133)
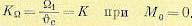
Здесь введено понятие так называемой добротности по моменту (или крутизны по моменту), которая равна отношению приведенного к оси двигателя момента нагрузки к возникающей при этом статической (моментной) ошибке:
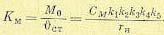 (5.134)
(5.134)
Из формулы (5.133) видно, что в неподвижном положении ошибка определяется только моментом нагрузки (возмущающим воздействием). Это означает, что рассматриваемая система обладает астатизмом относительно управляющего воздействия
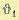 и статизмом относительно возмущающего воздействия М.
и статизмом относительно возмущающего воздействия М.
Заметим, что в формулу (5.133) входит момент нагрузки, приведенный к валу двигателя. Поэтому в эту формулу не вошло передаточное отношение редуктора. Если перейти к моменту нагрузки оси управляемого объекта, то в знаменателе последнего выражения (5.133) появится в качестве множителя i. В соответствии с этим можно сформулировать другое понятие добротности по моменту, как отношение момента нагрузки на оси управляемого объекта к установившейся ошибке.
При движении с постоянной скоростью  = const и М = М0 = const из (5.132) получается установившаяся ошибка
= const и М = М0 = const из (5.132) получается установившаяся ошибка
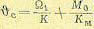 (5.135)
(5.135)
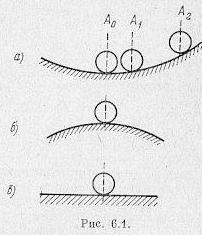
Здесь можно ввести понятие добротности по скорости, которая является коэффициентом пропорциональности между скоростью движения следящей системы и возникающей при этом установившейся ошибкой (при отсутствии возмущения). В данном случае она равна общему коэффициенту усиления по разомкнутой цепи:
ГЛАВА 6. КРИТЕРИИ УСТОЙЧИВОСТИ.
§ 6.1. Понятие об устойчивости систем регулирования
Понятие устойчивости системы регулирования связано со способностью возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния. Наглядно устойчивость равновесия иллюстрируется рис. 6.1, а, на котором изображен шар, лежащий в некотором углублении. При всяком отклонении его от положения равновесия он будет стремиться возвратиться к нему точно (при отсутствии сил трения) или к некоторой конечной области, окружающей предшествующее положение равновесия (при наличии сил трения). Такое положение шара будет устойчивым.
На рис. 6.1, б изображен другой случай, когда положение шара оказывается неустойчивым. Рис. 6.1, в соответствует случаю безразличного положения равновесия.
Можно ввести понятия о невозмущенном состоянии равновесия, соответствующем точке А0 на рис. 6.1, а, и возмущенном состоянии равновесия (точка А2). После прекращения действия внешних сил шар возвратится в точку А0 или А1. Условие устойчивости здесь можно сформулировать так: система называется устойчивой, если из возмущенного состояния равновесия она перейдет в некоторую конечную область, окружающую невозмущенное состояние равновесия.
Понятие устойчивости можно распространить и на случай движения некоторой системы. Пусть ее состояние определяется независимыми координатами x1 (t), х2 (t), ..., хn(t). Заданное движение системы определяется некоторым законом изменения координат:
х10 (t), х20 (t), . . ., хn0 (t).
Аналогично случаю равновесия положения заданное движение можно назвать невозмущенным движением. Приложение внешних сил к рассматриваемой системе вызовет отклонение действительного движения от заданного: x1(t) ≠ x10(t), х2(t) ≠ х20(t) и т. д. Это движение будет возмущенным.
Заданное невозмущенное движение будет устойчивым, если в результате приложения внешних сил, которые затем снимаются, возмущенное движение по истечении некоторого времени войдет в заданную область:
 .
.
Рассмотрим вопрос устойчивости более подробно. Пусть система регулирования описывается нелинейными дифференциальными уравнениями в форме Коши
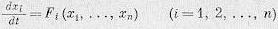 (6.1)
(6.1)
Если при t = t0 заданы начальные значения хi0 (i = 1, 2, . . ., n), ( то решение может быть представлено в виде 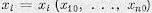 ), где i = 1, 2, . . ., n.
), где i = 1, 2, . . ., n.

Пусть установившиеся процессы в системе характеризуются координатами
 . Введем также отклонения координат
. Введем также отклонения координат 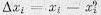 (i = 1, . . ., n), характеризующие отклонения процесса от установившегося.
(i = 1, . . ., n), характеризующие отклонения процесса от установившегося.
Систему уравнений (6.1) перепишем для отклонений:
где fi — некоторые нелинейные функции. Эти уравнения называются уравнениями
возмущенного движения. Их тривиальные решения 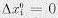 соответствуют невозмущенному движению, так как при этом
соответствуют невозмущенному движению, так как при этом  .
.
Начальные значения отклонений 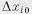 носят название возмущений. Решение системы (6.2) для некоторых начальных отклонений
носят название возмущений. Решение системы (6.2) для некоторых начальных отклонений  представляет собой возмущенное движение.
представляет собой возмущенное движение.
А. М. Ляпунов [82] дал следующее определение устойчивости.
Невозмущенное движение (при 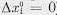 ) называется устойчивым по отношению к переменным жг, если при всяком заданном положительном числе А2, как бы мало оно ни было, можно выбрать другое положительное число
) называется устойчивым по отношению к переменным жг, если при всяком заданном положительном числе А2, как бы мало оно ни было, можно выбрать другое положительное число 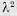 (А2) так, что для всех возмущений
(А2) так, что для всех возмущений 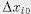 , удовлетворяющих условию
, удовлетворяющих условию
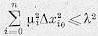 (6.3)
(6.3)
возмущенное движение (6.2) будет для времени 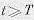 удовлетворять неравенству
удовлетворять неравенству
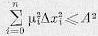 (6.4)
(6.4)
Здесь 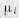 , — некоторые весовые коэффициенты, необходимые для уравнивания физических размерностей величин
, — некоторые весовые коэффициенты, необходимые для уравнивания физических размерностей величин 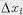 .
.
Геометрическая интерпретация этого условия заключается в следующем. В пространстве координат 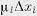 ; достроим две сферы с радиусами
; достроим две сферы с радиусами  и А. Система будет устойчивой, если при возмущениях, не выведших изображающую точку М (
и А. Система будет устойчивой, если при возмущениях, не выведших изображающую точку М ( ) из пределов сферы
) из пределов сферы 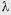 , возмущенное движение будет таково, что, начиная
, возмущенное движение будет таково, что, начиная
с некоторого времени  , изображающая точка М (
, изображающая точка М ( ) будет в пределах сферы А.
) будет в пределах сферы А.
Если с течением времени изображающая точка стремится к началу координат, т. е.
то система асимптотически устойчива.
Несколько другое изложение этой теоремы будет дано ниже в § 16.1. Перейдем теперь к вопросу устойчивости линейных, а точнее, линеаризованных
систем регулирования.
Рассмотрим дифференциальное уравнение движения линеаризованной системы автоматического регулирования, записанное для регулируемой величины у (t) при наличии управляющего воздействия g (t) и при равенстве нулю возмущающих воздействий:
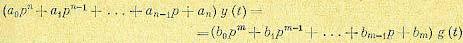 (6.5)
(6.5)
Коэффициенты а0, . . ., аn и b0, . . ., bm представляют собой постоянные величины, а
оператор  .
.
Дифференциальное уравнение движения системы регулирования можно записать и для возмущающего воздействия. В этом случае левая часть (6.5) останется без изменения, а правая часть будет иметь иной вид. В общем виде дифференциальное уравнение, определяющее изменение регулируемой величины, может быть записано так, что в правой его части будет находиться некоторая функция времени f (t).
