Теория систем автоматического управления. В.А. Бесекерский, Е.П. Попов, 1975

передаточной функции W(z) амплитудно-фазовая характеристика становится

периодической функцией с периодом2πT −1 .

Пусть, например, дискретная передаточная функция разомкнутой системы имеет вид

(15.167)

Получим частотную передаточную функцию подстановкой z= еjwT:

(15.168)

В координатах u= ReW и v = ImW амплитудно-фазовая характеристика будет представлять собой вертикальную прямую линию, отстоящую влево от начала координат на величину 0,5 КТ. Граница устойчивости будет при прохождении этой прямой через точку (—1, j0). Отсюда можно получить условие устойчивости КТ < 2.

Получим теперь частотную передаточную функцию на основе w-преобразования. Для этого в формуле (15.167) применим подстановку (15.162). В результате получим передаточную функцию разомкнутой системы как функцию комплексной величины w:

(15.169)

Частотная передаточная функция разомкнутой системы при подстановке w = j T2 λ ,

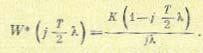(15.170)

Нетрудно видеть, что частотная передаточная функция (15.170) в зависимости от псевдочастоты имеет более простой вид по сравнению с (15.169). По выражению (15.170) может быть, в частности, просто построена асимптотическая л. а. х.

Подобным же образом могут быть получены дискретные передаточные функции Ф*(w) и Ф*x (w), а также частотные передаточные функции Ф*( j T2 λ ).

Оценка качества импульсной системы регулирования может делаться построением кривой переходного процесса, что при использовании z-преобразования осуществляется сравнительно легко (§ 15.2), а также посредством различных критериев качества. Наиболее простым является использование показателя колебательности, который может характеризовать запас устойчивости системы. Как и в случае непрерывных систем, получение заданного показателя колебательности сводится к требованию, чтобы амплитудно-фазовая характеристика системы не заходила в запретную зону, окружающую точку (—1, j0) в соответствии с рис. 8.27.

Установившаяся точность импульсной системы может оцениваться по коэффициентам ошибок. Аналогично непрерывным системам, начиная с некоторого момента времени ошибку импульсной системы регулирования можно представить в виде ряда

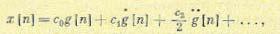(15.171)

где коэффициенты ошибок с0, с1, с2 и т. д. представляют собой коэффициенты разложения передаточной функции по ошибке Фх (z) в ряд Маклорена

по степеням р, т. е.

(15.172)

Величины, обратные множителям при производных выражения (15.171), по аналогии с непрерывными системами могут называться соответствующими добротностями. Например, добротность по скорости

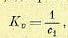(15.173)

добротность по ускорению

(15.174)

и т. д.

Вычислим, например, два первых коэффициента ошибок для системы с передаточной функцией разомкнутой цепи

где d = e−T / T1

Эта функция соответствует импульсному фильтру с передаточной функцией непрерывной части

и с приведенной передаточной функцией (15.136)

Находим передаточную функцию по ошибке:

Подстановка в это выражение р = 0 или г = 1 дает коэффициент с0 = О, Для получения коэффициента с1 находим первую производную:

Подстановка z = 1 дает коэффициент

а также добротность по скорости

Периодические режимы. Если на входе замкнутой импульсной системы (рис. 15.11) действует синусоидальная последовательность

то расчет синусоидальных последовательностей у [n] и х [n] может быть «делан на основе формул (15.152) и (15.154) при использовании передаточных функций замкнутой системы. Так, например, амплитуда ошибки (точнее, верхнее граничное значение синусоидальной последовательности для ошибки)

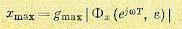(15.175)

и сдвиг по фазе

(15.176)

В общем случае негармонической периодической последовательности с периодом М (см. § 15.2) она может быть представлена в виде суммы конечного числа гармоник:

где N — целая часть M/2, а коэффициенты разложения

Для каждой гармоники в установившемся режиме может быть сделан расчет в соответствии с изложенным выше для синусоидальной последовательности. Поэтому в установившемся режиме для ошибки можно записать

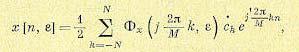(15.177)

где Фx ( j 2Mπ k,ε ) — значение частотной передаточной функции, полученное

j 2π k

из Фx (z, ε ) подстановкой z = e M .

Аналогичным образом по передаточной функции Ф (z, ε ) может быть получена для установившегося режима выходная величина у [n, ε ].

Более простой метод заключается в следующем. Рассмотрим, например, задающее воздействие g[n], представляющее собой периодическую последовательность, изображение которой (15.113)

где G0(z) — изображение g[n] на интервале 0 - М. Пусть рассматриваемая последовательность действует на входе системы с передаточной функцией Ф(z). Тогда изображение выходной величины

можно представить в виде суммы изображений переходной составляющей У° (z) и установившегося периодического режима У* (z). Первая составляющая определяется полюсами функции Ф (z) и с течением времени затухает, так как система предполагается устойчивой.

Периодическая составляющая на выходе может быть представлена в виде

где У*0 (z) — изображение у [n] на интервале 0 - М в установившемся режиме, которое и является искомой величиной, коэффициенты а0, . . ., аM-1 должны быть определены при разложении на сумму дробно-рациональных функций Y0 (z) и У* (z). Для этой цели могут использоваться известные методы, например теорема разложения. Так, если степень У1 (z) равна степени У2 (z) и У1 (z) = zУ3 (z), то

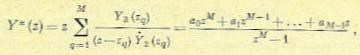(15.178)

где zq (q =1,..., M ) — корни уравнения zм -1 = 0.

Однако пользоваться этой формулой при М > 2 практически неудобно. При М >1 удобнее найти переходную составляющую У* (z), а затем периодическую: У* (z) = У (z) — У° (z). Далее можно найти

(15.179)

Так как полюсы Ф (z) известны, то отыскание переходной составляющей не представляет труда. Так, например, если степень числителя У (z) меньше степени знаменателя и полюсы Ф (z) не кратные, то

где zi (i =1,2, ...,l) — полюсы Ф(z).

Если степень числителя У (z) одинакова со степенью знаменателя, но числитель имеет общий множитель г, то можно записать

Тогда

Другие возможные случаи — см. § 15.2, п. 13.

Если входное воздействие представляет собой симметричную периодическую последовательность с полупериодом N, изображение которой дается формулой (15.114), то аналогичная зависимость для изображения периодической последовательности выходной величины на интервале 0 - N будет

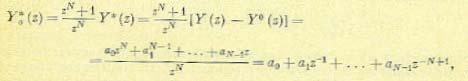(15.180)

где У° (z) — переходная составляющая, определяемая полюсами Ф (z).

Пример. Рассмотрим входную последовательность в виде прямоугольной волны (рис. 15.10, в), но с полупериодом N = 3 и систему с передаточной функцией

Изображение периодической последовательности на входе (15.114)

Найдем периодический режим на выходе. В соответствии с (15.180), учитывая, что Ф (z) имеет единственный полюс z1 = 0, имеем

Отсюда следует, что в установившемся периодическом режиме на выходе, если совместить начало положительного полупериода с началом отсчета, будет у [0] = 1 + а, у [1] = у [2] = 1 - а. В следующем полупериоде будет у [3] = -у [0] = - (1 + а), у [4] = у [5] = -у [1] = -(1 - а) и т. д.

§ 15.5. Случайные процессы в импульсных системах

Введем понятие случайной решетчатой функции f[n], которую можно образовать из непрерывной случайной функции f(z) ее дискретизацией. В этом случае она будет определена в дискретные моменты времени t= nТ. Будем рассматривать стационарные процессы, когда вероятностные характеристики не зависят от времени.

Среднее значение решетчатого случайного стационарного процесса

(15.181)

или на основании эргодического свойства

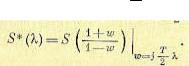
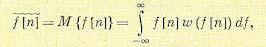(15.182)

где w(f[n]) — одномерная плотность вероятности.

Для центрированных процессов среднее значение равно нулю. Введем понятие

корреляционной функции

(15.183)

Аналогично главе 11 можно сформулировать основные свойства корреляционной функции.

1. Для случая m = 0

(15.184)

2. При m = 0 корреляционная функция достигает наибольшего значения:

(15.185)

3. Корреляционная функция является четной:

(15.186)

При наличии двух случайных процессов f1 [n] и f2 [n] можно ввести понятие взаимной корреляционной функции

(10.187)

Свойства ее схожи со свойствами взаимной корреляционной функции для непрерывных процессов.

Введем понятие спектральной плотности случайного стационарного решетчатого процесса как двустороннего z-преобразования корреляционной функции

(15.188)

где Т — нормирующий множитель, равный периоду дискретности, а F(z) представляет собой z-преобразование корреляционной функции R[m]. Нормирующий множитель Т введен в (15.188) для того, чтобы сделать физическую размерность спектральной плотности дискретного случайного процесса равной размерности спектральной плотности непрерывного процесса и сохранить ее физический смысл.

Аналогично непрерывному случаю можно ввести понятие спектральной плотности как функции круговой частоты

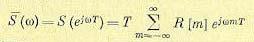(15.189)

или при учете четности

(15.190)

Наконец, можно определить спектральную плотность как функцию абсолютной псевдочастоты. Для этого в формуле (15.188) необходимо перейти к w-преобразованию, используя подстановку (15.163), а затем перейти к псевдочастоте посредством

подстановки w = j T2 k . В результате получим

(15.191)

Аналогичным образом может быть определена взаимная спектральная плотность двух процессов.

Заметим, что все приведенные формулы могут быть записаны и для случая ε ≠ 0 , тогда рассматривается случайная решетчатая функция f[n,ε ], корреляционная функция R[m, ε ],

спектральные плотности S (z, ε ), S (w, ε ) и S* ( λ Я, ε ).

Основное свойство спектральной плотности, как и в непрерывном случае, заключается в том, что интеграл от нее по всем частотам дает средний квадрат случайной величины. Можно показать [136], что в дискретном случае соответствующая формула имеет вид

(15.192)

Так как имеют место равенства

то формула (15.192) может быть записана в виде

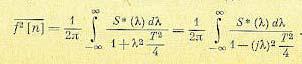(15.193)

Выражение (15.193) обычно является более удобным для расчетов по сравнению с (15.192), так как позволяет использовать таблицы интегралов-(см. приложение 2).

Типовые случайные стационарные процессы. Если для функции f(z), представляющей собой центрированную помеху, эффективное время корреляции

(15.194)

меньше периода дискретности, ∆τ <T , то такой процесс может быть представлен как дискретный белый шум с корреляционной функцией

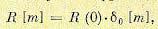(15.195)

где R[0] = D — дисперсия, а δ 0 [m] — единичная решетчатая импульсная функция (15.32), равная единице при m = 0 и равная нулю при m ≠ 0 . Этому белому шуму соответствует спектральная плотность

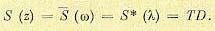(15.196)

Если эффективное время корреляции ∆τ >T , то корреляционная функция R [m] может быть получена из соответствующей корреляционной функции непрерывного процесса R(τ ) заменой τ = mT . Спектральная плотность может быть получена использованием формул (15.188) — (15491).

В табл. 15.2 приведены некоторые типовые дискретные стационарные случайные процессы.

Прохождение сигнала через линейную систему. Пусть на входе линейного звена с известной дискретной передаточной функцией W(z) действует случайная функция х1 [n],

для которой известны корреляционная функция R1 [m] и спектральная плотность S1 (w)

или S*( λ ). Тогда для выходной, величины х2[n], аналогично непрерывному случаю, можно найти спектральную плотность умножением спектральной плотности входного сигнала на квадрат модуля частотной передаточной функции:

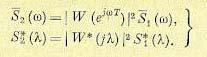(15.197)

Интегрирование спектральной плотности по всем частотам в соответствии с (15.192) и

(15.193) позволяет найти средний квадрат выходной величины x22 [n] . Это позволяет для

замкнутой импульсной системы производить расчеты, аналогичные изложенным в § 11.8. Так, например, пусть в схеме, изображенной на рис. 15.11, на входе действуют полезный сигнал g(t) и помеха n(t), не коррелированные между собой. Обозначим их спектральные

плотности S g* (λ) и Sn* (λ) . Тогда спектральная плотность ошибки

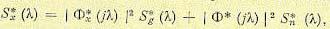(15.198)

где Ф*(j λ ) и Ф*x (j λ ) — частотные передаточные функции замкнутой системы и замкнутой системы по ошибке.

Интегрирование (15.198) по всем частотам в соответствии с (15.193) дает средний квадрат ошибки

(15.199)

Подобным же образом могут быть найдены расчетные формулы и для других возможных случаев (см. § 11.8).

РАЗДЕЛ IV

НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

ГЛАВА 16

СОСТАВЛЕНИЕ УРАВНЕНИЙ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

§ 16.1. Общие понятия

Нелинейной системой автоматического регулирования называется такая система, которая содержит хотя бы одно звено, описываемое нелинейным уравнением. Перечислим виды нелинейных звеньев;

1)звено релейного типа (рис. 1.12);

2)звено с кусочно-линейной характеристикой (рис. 1.10, д и др.);

3)звено с криволинейной характеристикой любого очертания;

4)звено, уравнение которого содержит произведение переменных или их производных и другие их комбинации;

5)нелинейное звено с запаздыванием, причем запаздывание понимается в смысле § 14,1, а нелинейность может иметь любой вид;

6)нелинейное импульсное звено;

7)логическое звено;

8)звенья, описываемые кусочно-линейными дифференциальными уравнениями, в том числе переменная структура.

Различают статические и динамические нелинейности. Первые представляются в виде нелинейных статических характеристик, а вторые — в виде нелинейных дифференциальных уравнений.

Общий метод составления уравнений для нелинейных систем состоит в следующем. Сначала по правилам § 3.1,-как делалось в главе 5, производится линеаризация уравнений всех звеньев системы, для которых это допустимо, кроме существенно нелинейных звеньев (чаще всего одного-двух). Затем составляются уравнения этих последних звеньев со всеми допустимыми упрощениями их характеристик.

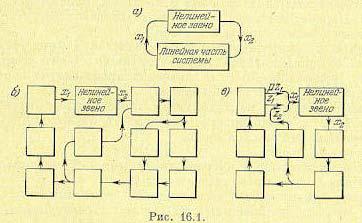
В результате получается система обыкновенных линейных уравнений, к которым добавляется одно-два (иногда более) нелинейных. В соответствии с этим обобщенную структурную схему любой нелинейной системы автоматического регулирования в случае одного нелинейного звена можно представить в виде рис. 16.1, а, где линейная часть может иметь структуру любой сложности (с обратными связями и т. п., как, например, на рис. 16,1, б или в). В случае двух нелинейных звеньев могут быть разные комбинации, в зависимости от того, в какие цепи системы они входят (см., например, рис. 16.2).

Часто при исследовании нелинейных систем автоматического регулирования удается выделить нелинейность так, чтобы она описывалась непосредственно зависимостью между выходной и входной величинами

(16.1)

которая может иметь любую форму (релейного типа, кусочно-линейного или криволинейного). Но иногда, как будет показано в следующих параграфах, не удается этого сделать и приходится исследовать нелинейные дифференциальные зависимости вида

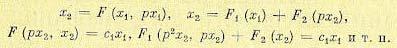(16.3)

Встречаются и более сложные случаи, когда обе величины (входная и выходная) оказываются под знаком нелинейной функции раздельно;

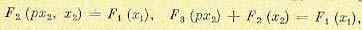(16.4)

или же вместе:

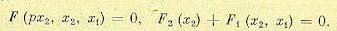(16.5)

Разделим все нелинейные системы регулирования на два больших класса.

1. К первому классу нелинейных систем отнесем такие, в которых уравнение нелинейного звена приводится к любому из видов (16.1) — (16.3), т. е. когда под знаком нелинейной функции стоит только входная величина (и ее производные) либо только выходная величина (и ее производные).При этом имеется в виду, что схема системы в целом может быть приведена к виду рис. 16.1 с одним нелинейным звеном. К этому классу сводится, например, также случай с двумя нелинейными звеньями, указанный на рис. 16.2, в, так как там они могут быть объединены в одно нелинейное звено. Сюда же относится и случай, показанный на рис. 16.2, г, где имеются два нелинейных звена (если их уравнения содержат под знаком нелинейности только входную величину х, например, вида (16.1) или

(16.2)).

2. Второй класс нелинейных систем включает системы с любым числом нелинейных звеньев, когда под знаки нелинейных функций входят различные переменные, связанные между собой линейной передаточной функцией. Так будет в случае системы с одним нелинейным звеном вида (16.4) или (16.5), а также в системе с двумя нелинейными звеньями (рис. 16.2, а или г), если в первом из них под знак нелинейности входит входная величина, а во втором — выходная. Система же рис. 16.2, б относится ко второму классу, если под знаки нелинейностей входят в обоих звеньях либо только входные, либо только выходные величины нелинейных звеньев.

Ко второму классу нелинейных систем относятся также системы с двумя и более нелинейностями, в уравнениях которых под знаки нелинейных функций входят разные переменные, связанные между собой нелинейными дифференциальными уравнениями (т. е. связанные через линейные части и нелинейные звенья). К таким системам относятся, например, система на рис. 16.2, а, если в ее уравнениях под знаками нелинейных функций находятся входные (или выходные) величины обоих нелинейных звеньев, и многие другие системы.

Системы с логическими устройствами относятся обычно к нелинейным системам второго класса.

Заметим, что во всех случаях, когда под знак нелинейной функции входит какая-либо линейная комбинация разных переменных, их следует обозначать одной буквой, а данную линейную комбинацию учесть при составлении общего уравнения линейной части системы. Это бывает, например, в тех случаях, когда на вход нелинейного звена подаются производные или включается обратная связь. Так, если для рис. 16.1, б

то, обозначая

можно привести уравнение нелинейного звена к виду (16.1).

Из всех уравнений линейных звеньев, а также добавочных линейных выражений типа (16.6), получаемых при выделении нелинейности, составляется общее уравнение линейной части системы

(16.7)

(где Q (р) и R(р) — операторные многочлены) или передаточная функция линейной части системы

(16.8)

Составление уравнений будет проиллюстрировано ниже на примерах. Процессы в нелинейных системах автоматического регулирования имеют целый ряд весьма существенных особенностей, которые не встречаются в линейных системах. Благодаря этим существенным особенностям даже вопрос об устойчивости системы

становится здесь более сложным. Кроме структуры системы и значений ее параметров для устойчивости того или иного установившегося процесса имеют значение здесь, в отличие от линейных систем, также и начальные условия. Возможен новый вид установившегося процесса _ автоколебания, т. е. устойчивые собственные колебания с постоянной амплитудой при отсутствии внешних колебательных воздействий. Когда в системе возникают автоколебания, то установившееся состояние, соответствующее постоянному значению регулируемой величины, часто становится невозможным.

Следовательно, в общем случае на плоскости параметров системы могут быть не два вида областей (устойчивости и неустойчивости), как в линейных системах, а больше: 1) область устойчивости равновесного состояния с постоянным значением регулируемой величины; 2) область устойчивых автоколебаний; 3) область неустойчивости системы; 4) области, соответствующие другим, более сложным случаям.