2.5.Потенциал заданного распределения заряда

Напряженность электростатического поля, создаваемого точечным зарядом q в некоторой точке, отстоящей от этого тела на расстоянии r определяется выражением (из закона Кулона):

.

Определим потенциал поля точечного заряда. Подставляя напряженность поля точечного заряда в (2.2), получим

,

.

Пусть фиксированная точка находится на бесконечности, т. е.

,

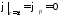тогда постоянная интегрирования в выражении равна нулю:

.

В этом случае формула для потенциала произвольной точки поля точечного заряда примет вид

.

Для потенциалов, как и для напряженностей, справедлив принцип наложения (суперпозиции):

Потенциал поля n неподвижных точечных зарядов равен:

.

В случае непрерывного распределения заряда с учетом имеем:

–для объемного распределения заряда,

–для поверхностного распределения,

–для линейного распределения заряда.

При решении задач электростатики обычно рассчитывается потенциал в точках поля, а затем определяется напряженность в этих точках.

2.5.1.Потенциал и напряженность электрического поля диполя

Рассмотрим систему из двух разноименных, но равных по абсолютной величине точечных зарядов, находящихся на расстоянии l. Ее электрическим моментом является вектор

где q – абсолютная величина каждого заряда,

–вектор с абсолютным значением l и направленный от положительного заряда к отрицательному.

Поле этой системы будем исследовать на расстояниях r, значительно превышающих ее размер

r >> l.

Потенциал диполя в произвольной точке М равен

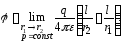
Полагая в соответствии с рисунком,

r₁r₂→r² и r₁ – r₂ → l∙cos(θ),

находим:

Теперь по формуле можно определить поле диполя. Это проще всего сделать, пользуясь сферической системой координат

получаем

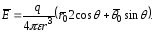
Как и следовало ожидать, поле диполя симметрично относительно его оси. Силовые линии поля в меридиональной плоскости изображены на рисунке.

2.6.Уравнение Пуассона и Лапласа

Расчет электростатических полей с использованием уравнений ивозможен только в простейших случаях. Наиболее общим методом является расчет электро­статических полей на основе решения уравнений Пуассона и Лапласа относительно потенциала. Выве­дем эти уравне­ния.

Ранее было получено 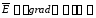. Тогда:

, откуда следует:

или

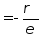. (2.5)

Уравнение (2.5) называется уравнением Пуассона. – Лапласиан.

В декартовой системе координат может быть представлено в форме

.

Уравнение Пуассона справедливо для тех точек среды, где существуют объемные за­ряды .

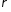Решение уравнения Пуассона в общем виде можно найти следующим образом. Положим, что в объеме V есть объемные  заряды. Эти заряды представим в виде совокупности точечных зарядов: dV, где dV – элемент объема. Составляющая потенциала d электрического поля от элементарного заряда dV равен

.

Значение  определяется как сумма (интеграл) их потенциала от всех зарядов поля:

Предполагается, что потенциал на бесконечности равен нулю и заряды, создающие поля распределены в ограниченной области (иначе интеграл может оказаться расходящимся).

В реальных условиях свободные заряды располагаются на поверхности проводников бесконечно тонким слоем.

В диэлектриках, которыми разделены заряженные проводники, объемные заряды от­сутствуют , уравнение Пуассона в диэлектрике превращается в уравнение Лапласа:

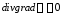
или

.