Вопросы для самопроверки

1. Как определяют векторный магнитный потенциал?

2.Везде ли можно определить скалярный магнитный потенциал?

3. Как изменяется напряженность магнитного поля при переходе из одной среды в другую?

4. В чем различие картин электрического поля заряженного проводника и магнитного поля проводника с постоянным током в нем?

5. Переменное электромагнитное поле

Под переменным электромагнитным полем понимают совокупность изменяющихся во времени и взаимно связанных друг с другом электрического и магнитного полей.

При исследовании процессов в переменном электромагнитном поле пользуются уравнениями, которые принято называть уравнениями Максвелла. Ниже получены уравнения электромагнитного поля, изменяющегося по гармоническому закону.

5.1. Уравнения Максвелла в комплексной форме

Если векторы поля иизменяются во времени по синусоидальному закону, то синусоидальные функции времени могут быть представлены комлексными числами и, со­ответственно, сами векторы будут комплексными:

В записанных выражениях черта снизу символа означает «комплекс», а черта сверху – «вектор», соответственно читается «комплекс-вектор».

Учитывая, что операции дифференцирования в комплексной форме соответствует умножение комплексного изображения на множитель 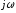, то в урав­нениях Максвелла в комплексной форме время, как координата, в явной форме отсутствует.

С учетом принятых обозначений система основных уравнений Максвелла в ком­плексной форме получит вид:

Комплексный вектор Пойтинга можно представить по аналогии с комплексной мощ­ностью:

.

Теорема Умова-Пойтинга в комплексной форме (без вывода):

.

Здесь 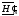- сопряженный комплекс амплитуды вектора напряженности магнитного поля.

5.2 Плоская гармоническая волна в диэлектрике

Плоской называется электромагнитная волна с плоским фронтом, у кото­рой векторы поля 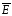ивзаимно перпендикулярны и при соответствую­щем выборе направления осей координат будут зависеть только от одной про­стран­ственной координатыz и времени t.

Волна называется гармонической, если век­торы поля иизменяются во времени по синусоидальному за­кону.

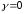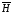Волна распространяется в однородном диэлектрике (ε), прово­димость которого равна нулю ().Выберем направления осей координатx, y, z так, чтобы вектор совпа­дал с осьюx , векторсовпадал с осьюy , тогда вектор Пой­тинга будет направлен вдоль осиz.

Система уравнений Максвелла в комплексной форме:

Раскроем операцию rot в декартовой системе координат и учтем, что

векторы поля содержат только по одной пространственной составляющей: ,:

.

.

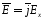Таким образом, система уравнений Максвелла получит вид:

Решим данную систему дифференциальных уравнений относительно одной из пере­менных, например, . Для этой цели продифференцируем уравнение (2) по пе­ременнойz и выполним в него подстановку из уравне­ния (1):

,

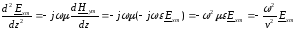где  фазовая скорость волны.

Таким образом,

Решение для искомой функции:

где  корни характеристического уравнения.

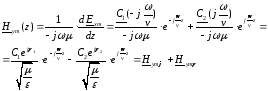
- волновое сопротивление.

Решение содержит электромагнитные волны:

прямую - H_ymφ; E_xmψ=Z_B H_ymφ; обратную - H_ymψ; E_xmψ=Z_B H_ymψ;

В неограниченной однородной среде отраженные волны отсутствуют, поэтому при­мем С₂=0, С₁=Сe^j, тогда решение для искомой функции получит окончательный вид:

где .

Решение для переменной получим из уравнения (2) путем подстановки в него найденного решения для переменной: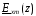

,

где - волновое сопротивление среды;

для пустоты Ом.

Перейдем от комплексного изображения функций к их оригиналам:

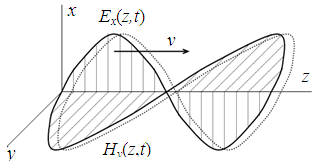
Таким образом, электромагнитное поле в диэлектрике распространяется в виде незату­хающих взаимно перпендикулярных в пространстве волн исо скоростью.

Отношение мгновенных значений волн 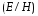в любой точке простран­ства и в любой момент времени постоянно и равно волновому сопротивлению.

Длиной волны λ называют расстояние, на котором фаза волны изменяется на 2π:

откуда следует, что

Каждая из волн переносит энергию в направлении своего движения, при этом объемные плотности энергий электрического и магнитного полей равны между собой.