2.14.1. Поле уединенной равномерно заряженной оси

Под заряженной осью понимают весьма тонкий, теоретически бесконечно длинный металлический проводник, на котором равномерно распределен заряд с линейной плотностью .

Пусть заряженная ось находится в среде с относительной диэлектрической проницаемостью 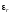. Заряд, приходящийся на единицу ее длины известен и равен. Требуется определить напряженность поля и потенциал в любой его точке, удаленной на расстояниеот оси.

Pасчитаем поле в произвольной точке M с помощью теоремы Гаусса в интегральной форме. Ось c линейным зарядом плотностью окружим цилиндрической поверхностью произволь­нного радиуса r и длиной обра­зующей l =1 так, чтобы ось цилиндра совпала с заряженной осью. Вектор электрического смещения 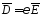в силу симметрии во всех точках на боковой поверхности цилиндра (r=const) имеет одно и то же значение и направление по ра­диусу, т.е. нормально к этой поверхности.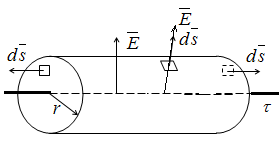

По теореме Гаусса .

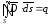Поток вектора через торцевые поверхности цилиндра равен нулю, так как линии вектора здесь направлены по касательной к поверхности. Тогда

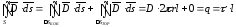
Откуда следует, что .

.

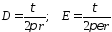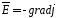В цилиндрической системе координат потенциал поля зависиь только от ра­диус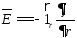а.:, откуда

.

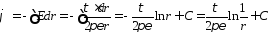Если принять на некоторой поверхности радиуса 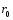значение потенциала равным нулю, то 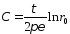и значение потенциала на поверхности произвольного радиуса бу­дет равна:

.

2.14.2. Метод наложения. Поле двух параллельных разноименно заряженных осей

Две разно­именно заряженные оси 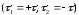расположены параллельно на расстоянии 2b в ди­электрическом пространстве.

Результирующий вектор напряженности поля равен геометрической сумме составляющих, а результирующий потенциал – ал­гебраической сумме составляющих от каж­дого провода:

.

Если принять 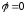в точках равноудалённых от обеих осей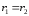, то постоянная интегрирования будет равна нулю (С=0).

Тогда получим: .

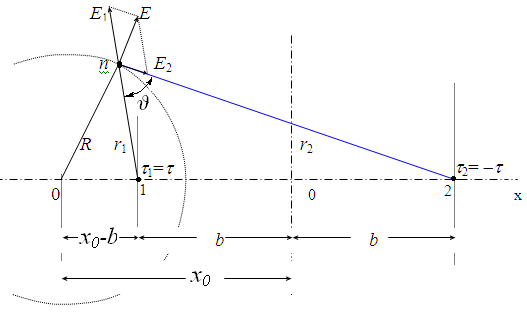
Рис.2.6

Эквипотенциальные поверхности должны удовлетворять условию .

Теорема Аполония гласит, что гео­метрическим местом точек, отношение расстояний от которых до заданной пары точек по­стоянно, является окружность, центр которой лежит на линии, соединяющей заданную пару точек.

Анализ геометрии (рис.2.6) показывает, что треугольник 20n подобен тре­угольнику n01 (общий угол с вершиной 0 и прилежащие к углу стороны про­порциональны). Из подобия треугольников следует:

.

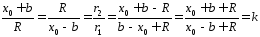При перемещении точки n вдоль окружности изменяются расстояния и 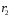так, что их отношение остается постоянным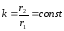. При изменении отношенияцентр окружности перемещается вдоль линии, соединяющуй заданную пару точек 1 и 2.

Координаты центра окружности равны: y₀=0.

Радиус окружности - .

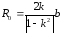Силовые линии - линии вектора напряженности поля 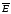являются ортогональными линиям равного потенциала. Поэтому силовые линии являются дугами окружно­сти, но с цен­трами, расположенными на вертикальной оси симметрии. Уравнением дуги окружности являетсяυ=const (рис.2.6).

Координаты центра окружности: x₀=0;;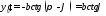

Радиус окружности: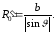

Рис.2.7

Картиной поля называется совокупность сле­дов эквипотенциальных поверхностей с заданными значениями потенциалов, построенная совместно с силовыми линиями (рис.2.7).