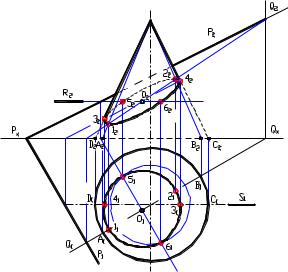
Рисунок 8.24

Промежуточные точки определятся во вспомогательных плоскостях (Ri) перпендикулярных оси вращения.

Сопряженная "малая" ось эллипса 56 может быть получена в плоскости R проходящей через точку О

середину отрезка 12 (большая ось эллипса).

В общем случае промежуточные точки могут быть найдены и другим способом.

Подводя итог рассмотренным решениям, можно отметить, что линии пересечения строятся по точкам, которые на поверхности можно зафиксировать, введя дополнительные плоскости. Этот подход и определяет общую методику построения линии пересечения поверхностей.

8.4.2 Способ секущих плоскостей

Этот способ применяют для построения линии пересечения поверхностей, позволяющих получать (одновременно) во вводимых секущих плоскостях, графически простые линии (прямые или окружности). Это утверждение может быть проиллюстрировано на примере

пересечения цилиндра и конуса Ф рисунок 8.25.

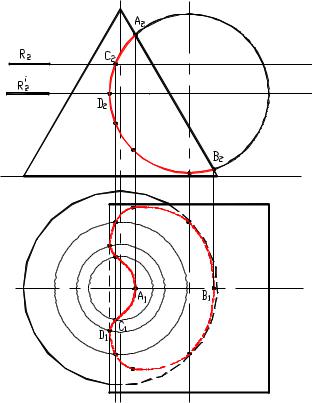
Рисунок 8.25

Здесь в качестве вспомогательных секущих плоскостей выступают горизонтальные плоскости уровня

Ri. На поверхности конуса (в силу того, что они

перпендикулярны оси вращения) эти плоскости выделяют окружности, а на поверхности цилиндра параллельные прямые (образующие).

Экстремальные (высшая и низшая) точки А, В линии пересечения определяют в пересечении фронтальных очерков. Граница видимости определится меридианом конуса вращения.

Текущие точки линии пересечения определятся, как результат пересечения соответствующих окружностей и

прямых в секущих плоскостях Ri.

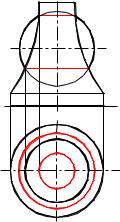
8.4.3 Способ секущих сфер

Рисунок 8.26

Этот способ базируется на том, что две соосные поверхности вращения пересекаются по окружности, лежащей в плоскости перпендикулярной общей оси вращения.

Сфера будет соосна с любой поверхностью вращения, если ее центр лежит на оси вращения этой поверхности (рисунок 8.26). Это и определяет возможность использовать сферу в качестве вспомогательной секущей поверхности.

Условием применения сферы в этом качестве является следующее: рассматриваются поверхности вращения, их оси должны пересекаться в одной точке центре секущих сфер.

При этом желательно, чтобы плоскость, образованная пересечением осей была бы параллельна одной из плоскостей проекции.

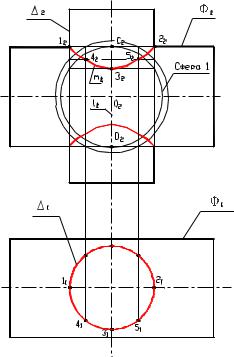
Рисунок 8.27

Линия пересечения двух цилиндров Ф и (RФ>R )

может быть определена с помощью метода секущих сфер. Это определяется тем, что выполняются все поставленные выше условия.

Линия пересечения распадается на две ветви, нижнюю и верхнюю, построение которых аналогично (рисунок 8.27).

Фронтальные проекции характерные точек линии пересечения 12 и 22 определятся, в результате

пересечения фронтальных очерков Ф2 и 2 ,а горизонтальные определятся по принадлежности этих точек цилиндру Ф.

Низшая точка линии пересечения определяется введением сферы RФ, которая пересечет цилиндр Ф по окружности l (фронтальная проекция этой окружности совпадет с фронтальной проекцией оси вращения

пересечения окружностей l и m.

Промежуточные точки определятся аналогично, как пересечение окружностей, получающихся в пересечении