
- •Предисловие
- •Введение
- •1 Конструктивное отображение пространства
- •1.1 Проецирование
- •1.2 Моделирование трехмерного пространства
- •1.3 Комплексный чертеж (Эпюр Монжа)
- •2 Чертежи точки, отрезка прямой
- •2.1 Комплексные чертежи точки
- •2.2 Комплексные чертежи прямых
- •2.3 Следы прямой
- •2.4 Взаимное расположение прямых
- •3 Чертежи плоскости
- •4 Позиционные задачи
- •4.1 Принадлежность точки и прямой
- •4.2 Пересечение плоскостей
- •4.3 Пересечение прямой и плоскости
- •4.4 Параллельность
- •5 Метрические задачи
- •5.1 Определение длины отрезка
- •5.2 Определение площади треугольника
- •5.3 Проецирование прямого угла
- •5.4 Перпендикулярность прямых и плоскостей
- •5.4.1 Перпендикулярность прямой и плоскости
- •5.4.2 Перпендикулярность плоскостей
- •6 Преобразование чертежа
- •6.1 Перемена плоскостей проекции
- •6.2 Преобразование прямой
- •6.3 Преобразование плоскости
- •6.4 Вращение вокруг следа плоскости
- •6.5 Применение преобразования плоскости
- •7 Кривые линии
- •7.1 Дифференциальные характеристики кривой
- •7.2 Особые точки кривых
- •7.3 Алгебраические кривые
- •7.4 Конические сечения
- •7.5 Плоские обводы
- •7.6 Пространственные кривые
- •8 Поверхности
- •8.1 Задание поверхности на чертеже
- •8.2 Точка и линия на поверхности
- •8.3 Конструирование поверхностей
- •8.3.1 Конструирование поверхностей вращения
- •8.3.3 Конструирование линейчатых поверхностей
- •8.3.4 Многогранники
- •8.4 Поверхности и позиционные задачи
- •8.4.1 Сечение поверхности плоскостью
- •8.4.2 Способ секущих плоскостей
- •8.4.3 Способ секущих сфер
- •8.4.4 Пересечения многогранников
- •8.5 Пересечение линии и поверхности
- •9 Аксонометрические проекции
- •9.1 Прямоугольная аксонометрия
- •9.2 Практические аксонометрии
- •10 Развертки поверхностей
- •10.1 Развертки гранных поверхностей
- •10.2 Приближенное построение разверток
- •10.3 Условные развертки поверхностей
- •11 Решение задач в Начертательной геометрии
- •11.1 Точки и прямые
- •11.2 Плоскости
- •11.3 Поверхности
- •11.4 Аксонометрические проекции
- •Список использованных источников
- •Приложение А
По этой схеме могут быть получены такие поверхности, как цилиндр общего вида (рисунок 8.10, плоскость (образующая и направляющая прямые линии), параболический параболоид (рисунок 8.11) и другие.
8.3.3Конструирование линейчатых поверхностей
Линейчатые поверхность образуются при движении
прямой линии (образующей) по заданному закону. Закон движения обычно задается направляющими. В качестве направляющих обычно рассматривают линии. Хотя направляющими могут быть и поверхности (образующая перемещается, касаясь этой поверхности) и другие геометрические элементы.
Например, коническая поверхность образуется при движении прямолинейной образующей, проходящей через фиксированную точку (вершину) и пересекающей направляющую кривую. Коническая поверхность с несобственной вершиной называют цилиндрической поверхностью.
Из определения линейчатой поверхности следует, что ее образующая в каждый момент времени должна занимать строго определенное положение. Такое возможно только при наличии трех направляющих. Поэтому линейчатые поверхности называются еще поверхностями с тремя направляющими.
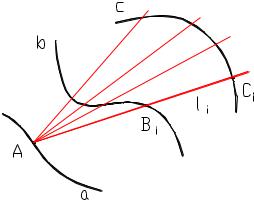
Рисунок 8.12
Действительно, взяв на направляющей a произвольную точку А, мы можем провести через нее, по крайней мере, одну образующую l, пересекающую другие две направляющие Ь, с. Точка А и направляющая Ь
определяют коническую поверхность (рисунок 8.12),которую направляющая с пересекает в нескольких точках Сi. Прямые AСi, очевидно, пересекают направляющую Ь. Таким образом, при перемещении точки А по кривой а прямые AСi опишут линейчатую поверхность.
Эти направляющие: а, Ь, с и входят в определитель линейчатой поверхности с тремя направляющими, что символически записывается так:
Ф(а,Ь,с).
Среди линейчатых поверхностей выделяют поверхности с плоскостью параллелизма. Их также
называют поверхностями Каталана. Образующие l этих поверхностей пересекают направляющие кривые а, b и параллельны плоскости параллелизма Г - собственному
представителю несобственной направляющей прямой с∞.
В зависимости от вида направляющих а, b поверхность с плоскостью параллелизма называется цилиндроидом, коноидом или косой плоскостью.
Цилиндроидом называется линейчатая поверхность с плоскостью параллелизма, у которой направляющие - кривые линии.
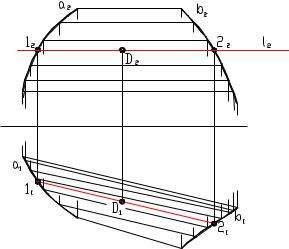
Рисунок 8.13 |
Каркас образующих цилиндроида на комплексном чертеже строится весьма просто, если в качестве
плоскости параллелизма принята одна из плоскостей проекций или проецирующая плоскость. На рисунке 8.13 построен каркас образующих цилиндроида с
направляющими а, b и параллельными плоскости параллелизма П1 . Образующие являются горизонталями.
Коноидом называется линейчатая поверхность с плоскостью параллелизма, имеющая одну криволинейную и вторую прямолинейную направляющие.
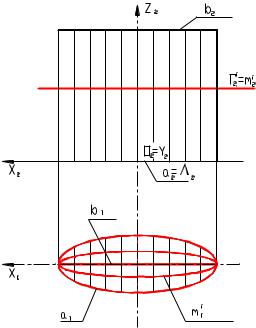
Рисунок 8.14 |
На чертеже коноид задается аналогично цилиндроиду. Построение каркаса образующих не отличается от цилиндроида.
На рисунке 8.14 приведен чертеж коноида, получившего в инженерной практике название "прямой клин".
Направляющими коноида являются эллипс а и прямая Ь, плоскость параллелизма zOy. Эта поверхность несет на себе каркас эллипсов в плоскостях параллельных П1.
Косой плоскостью называется линейчатая поверхность с плоскостью параллелизма и прямолинейными направляющими рисунок 8.15.
Она больше известна под названием гиперболического параболоида, так как несет на себе каркас не только прямых, но и гипербол и парабол. Из аналитической геометрии известно, что гиперболический
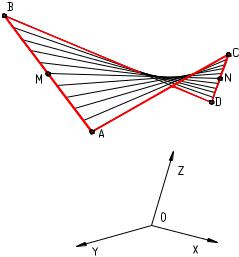
параболоид содержит два семейства прямолинейных образующих, параллельных двум плоскостям параллелизма.
Рисунок 8.15
Линейчатая поверхность, образованная множеством касательных к пространственной кривой, получила называние торсовой или поверхностью с ребром
возврата. Направляющая кривая t поверхности
называется ребром возврата t. Примером торсовой поверхности может служить хорошо известная коническая поверхность, у которой ребро возврата выродилось в точку (вершину конуса).
8.3.4 Многогранники
Многогранником называется тело, ограниченное плоскими многоугольниками. Поверхность, ограничивающая многогранник - составная. Элементами этой поверхности являются вершины, ребра и грани; совокупность всех ребер многогранника называют его сеткой. Многогранник называется выпуклым, если весь он лежит по одну сторону от плоскости любой его грани; тогда грани его - тоже выпуклые многоугольники.
Построение ограничивающей поверхности многогранника сводится к построению проекций ее сетки.
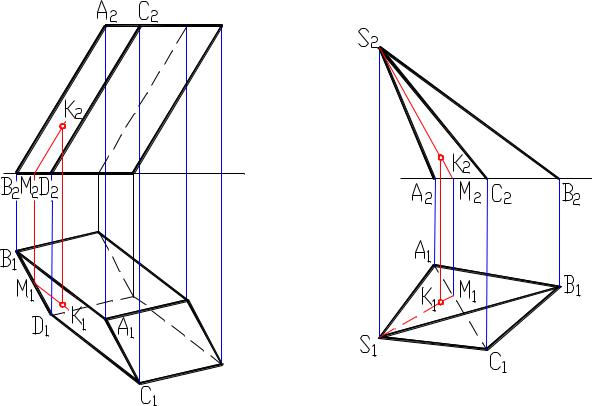
Рисунок 8.16 |
Рисунок 8.17 |
Среди всего многообразия многогранников наибольший практический интерес представляют призмы, пирамиды, призматоиды, а также правильные выпуклые многогранники.
Чертеж призмы приведен на рисунке 8.16. Гранями призмы служат четырехугольные отсеки плоскостей. Все ребра призмы параллельны между собой. Вопрос о принадлежности точки и линии ограничивающей поверхности сводится к определению принадлежности этих элементов плоским граням.
Пирамида (рисунок 8.17) ограничена составной поверхностью, у которой грани представлены треугольниками.
Все ребра пирамиды пересекаются в одной точке S, которую называют вершиной пирамиды.
Вопрос о принадлежности точки и линии ограничивающей поверхности, также сводится к определению принадлежности этих элементов плоским
граням.
Поверхность призмы можно рассматривать, как поверхность пирамиды, у которой вершина -
несобственная точка S∞.
8.3.5 Циклические и непрерывно-топографические
поверхности
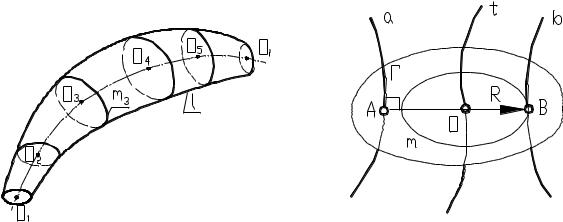
Циклической поверхностью называется поверхность, образованная непрерывным каркасом круговых сечений (рисунок 8.18). Циклическая поверхность несет на себе, по крайней мере, одно семейство круговых образующих. Циклическая поверхность является частным видом поверхностей подобных сечений.
Поверхностью подобных сечений принято называть поверхность, образованную непрерывным однопараметрическим множеством (каркасом) подобных плоских сечений.
Рисунок 8.18 - Поверхность подобных сечений Для однозначного определения поверхности подобных
сечений должны быть заданы три линии а, l и b, где, а - линия определяющая параметрическое семейство плоскостей перпендикулярных этой линии; l - линия
центров окружностей; b - линия,определяющая величины радиусов окружностей.
Примером таких поверхностей, имеющих круговые сечения, т. е. представляющим собой разновидность циклических поверхностей, могут служить эллиптический цилиндр, конус вращения, эллипсоид, однополостной и двуполостной гиперболоиды и др.
Кинематические поверхности сложной формы
традиционно называют поверхностями зависимых линий. Типичным представителем поверхностей зависимых линий являются топографические поверхности.
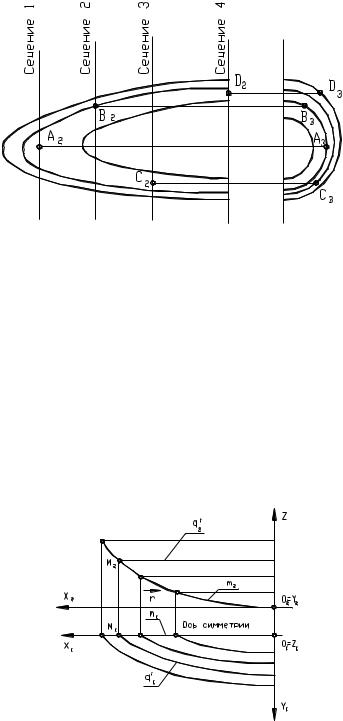
Рисунок 8.19 - Топографическая поверхность
Топографическими называют поверхности, заданные дискретным множеством линий уровня (рисунок 8.19). Такое представление поверхностей широко распространено в топографии, строительстве, военном деле и др. На ранних этапах развития авиации, автомобилестроения и судостроения сложные поверхности самолетов, автомобилей и судов задавались также в виде дискретного множества линий уровня. Получали сетчатый каркас поверхности, состоящий из трех семейств линий уровня: батоксов (вертикальных линий), горизонталей и поперечных сечений (шпангоутов).
Рисунок 8.20
Вопросы о принадлежности точки пространства для таких поверхностей решаются однозначно только на
