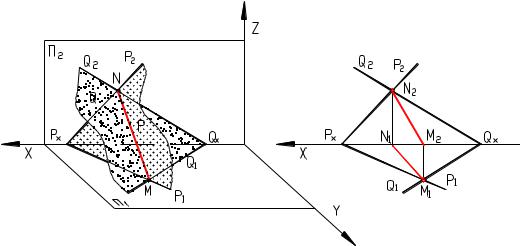
чтобы точка лежала на одной из прямых плоскости. |
Точка лежит С на прямой АВ (ее проекции, в |
соответствии с рисунком 4.2, лежат на одноименных |
проекциях прямой С1 А1В1, С2 А2В2). Прямая АВ Р, |
т.к. две ее точки принадлежат плоскости M Р, N Р. |
Последнее утверждение очевидно, вследствие того, что |
эти точки лежат на следах плоскости. Следовательно |
можно утверждать что С Р (рисунок 4.6). |
4.2 Пересечение плоскостей |
Рисунок 4.7 - Пересечение плоскостей |
В соответствии с p=2+2-3=1 пересечении двух плоскостей должно привести к появлению одномерного объекта, т.е. прямой линии. Для построения линии
пересечения двух плоскостей общего положения P и Q достаточно найти две точки, одновременно принадлежащие этим плоскостям. В случае задания плоскостей следами
(в соответствие с рисунком 4.7) решение очевидно. Пересечение горизонтальных следов P1 и Q1 дает
возможность определить положение одной общей точки N, а пересечение фронтальных следов P2 и Q2 другой общей
точки М. Линия NМ по определению лежит одновременно в двух плоскостях и следовательно она является линией пересечения.
Если одна из плоскостей проецирующая, (например, горизонтально проецирующая, в соответствии с рисунком
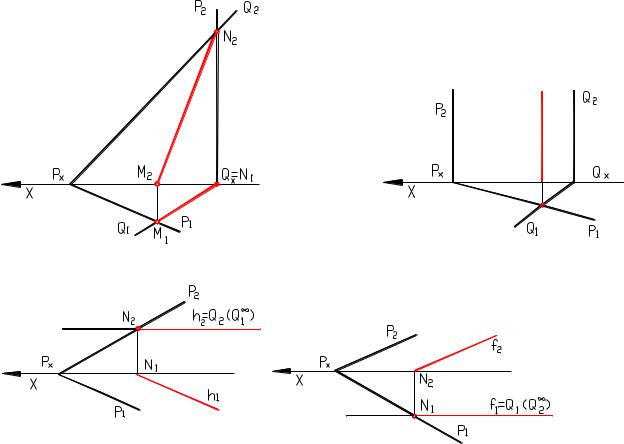
4.8), то линия пересечения может быть найдена из тех же самых соображений. Характерным здесь является то, что одна из проекций линии пересечения попадает на след проецирующей плоскости. Если обе плоскости - проецирующие, то и линия их пересечения - проецирующая.
Рисунок 4.8
Рисунок 4.9
При пересечении плоскости общего положения плоскостью уровня в сечении получается соответствующая линия уровня (рисунок 4.9). Определение линии пересечения двух плоскостей для других случаев, например, при задании плоскостей треугольником(симплексом) и параллельными прямыми, базируется на следующей идее. Три плоскости всегда пересекаются в одной точке. Следовательно, введение дополнительной плоскости к двум, уже имеющимся, позволит определить точку, одновременно принадлежащую заданным плоскостям. Проиллюстрируем это.
Две плоскости, заданные параллельными и
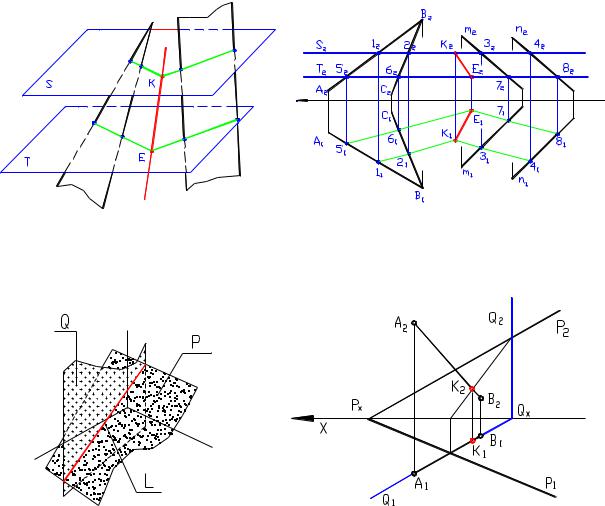
пересекающимися прямыми, пересекаются по прямой ЕК, найденной с помощью секущих плоскостей уровня S и Т.
Плоскость S пересекает (АВÇВС) по прямой 12, а плоскость (m//n) по прямой 34. На пересечении прямых 12 и 34 отмечается точка К. Аналогично строится точка Е, полученная с помощью секущей плоскости Т.
Рисунок 4.10
4.3 Пересечение прямой и плоскости
Рисунок 4.11 - Пересечение прямой с плоскостью
Пересечением прямой и плоскости в пространстве является точка, что подтверждается и вычислением
выражения для размерности пересечения p=1+2-3=0.
Прямая L в пространстве (в соответствии с рисунком 4.11) может рассматриваться как результат пересечения проецирующих плоскостей Q и Р. При этом проекции прямой нужно рассматривать как соответствующие следы этих плоскостей Q и Р.
Восстановление одной из проецирующих плоскостей,
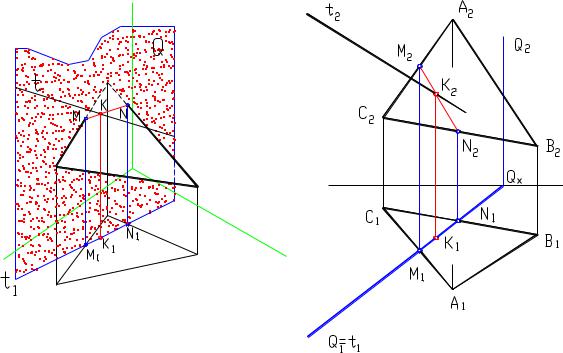
например, Q, в соответствии с рисунком 4.11 приведет к тому, что линия МN будет линией пересечения Q и Р. В силу этой особенности линия МN оказывается в одной плоскости с линией L. В пересечении этих прямых и будет лежать искомая точка К. Ее проекции лежат на проекциях линии L и, следовательно, она лежит на этой линии. С другой стороны, эта точка лежит на линии МN, принадлежащей плоскости Р , следовательно, искомая
точка пересечения - К.
Аналогичное решение этой задачи и в случае задания плоскости Р треугольником (симплексом). Восстановление одной из проецирующих плоскостей, например, Q, в соответствии с рисунком 4.12 приведет к тому, что линия МN будет линией пересечения Q и Р. В силу вышесказанного в пересечении прямых МN и t будет лежать искомая точка К. Она одновременно
принадлежит и плоскости АВС и t и, следовательно, К - искомая точка пересечения.
Рисунок 4.12 - Точка встречи прямой с плоскостью