3.Операції над подіями

Додавання. Сумою двох подій А і В називається така подія С=АВ (С=А + В), яка внаслідок експерименту настає з настаннямхоча б однієї з подій А або В. Подію АВ схематично зображено на рис. 1 заштрихованою областю.

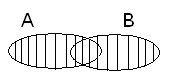
Рис. 1 Операція об 'єднання подій А і В.

Множення. Добутком двох подій А і В називається така подія С = АВ (С = АВ), яка внаслідок експерименту настає з одночасним настанням подій А і В.

Операція АВ називається перерізом цих подій (рис. 2).

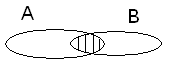
Рис. 2. Переріз подій А і В.

Приклад. Перерізом подій А = {2, 4, 6, 8, 10, 12} і В = {3, 6, 9, 12} є подія С₁ = {6}, а сумою є подія С₂ = {2, 3, 4, 6, 8, 9, 10, 12}.

Якщо , то випадкові події А і В називаютьнесумісними. Якщо , то такі випадкові події А і В називаютьсумісними.

Повна група подій. Якщо , то такі випадкові події утворюютьповну групу, а саме: внаслідок експерименту якась із подій {А_i} обов'язково настане.

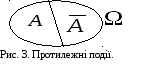
Протилежні події. Дві несумісні випадкові події, що утворюють повну групу, називають протилежними.

Подія, яка протилежна А, позначається . Протилежні події у просторі елементарних подій ілюструє рис. 3.

Елементарні випадкові події задовольняють такі твердження: 1) між собою несумісні; 2) утворюють повну групу; 3) є рівноможливими, а саме: усі елементарні події мають однакові можливості відбутися внаслідок проведення одного експерименту.

Питання для самоконтролю

1. Що називається вірогідною; неможливою подією? Навести приклади.

2. Яка подія називається випадковою? Навести приклади.

3. Яка подія називається елементарною; складеною випадковою подією? Навести приклади.

4. Що називається простором елементарних подій? Навести приклади.

5. Що називається сумою, добутком, різницею двох випадкових подій А і В?

Література

Обов’язкова: [1]. Додаткова:[1], [4], [7].

Тема 2. Основні теореми теорії ймовірностей, їх економічна інтерпретація

Мета роботи: вивчити поняття ймовірності події, залежних, незалежних, сумісних, несумісних подій; теореми додавання і множення ймовірностей, формули повної ймовірності, Байєса, умови їх застосування.

План вивчення теми

1. Класичне означення ймовірності.

2. Елементи комбінаторики.

3. Геометрична ймовірність.

4. Статистична ймовірність.

5. Умовна ймовірність.

6. Формули ймовірностей добутку та суми випадкових подій.

7. Імовірність появи хоча б однієї випадкової події.

8. Формула повної ймовірності.

9. Формула Байєса.

Методичні рекомендації до самостійної роботи

1. Класичне означення ймовірності

Для кількісного вимірювання появи випадкових подій і їх комбінацій вводиться поняття ймовірності події, що є числом такої ж природи, як відстань у геометрії або маса в теоретичній механіці.

Імовірністю випадкової події А називається невід'ємне число Р(А) що дорівнює відношенню числа елементарних подій які сприяють появі А до кількості всіх елементарних подій простору :

(2.1)

Для неможливої події (). Для вірогідної події. Отже, для довільної випадкової події(оскільки 0 <m < n).

Приклад. У ящику міститься 15 однотипних деталей, із яких 6 бракованих, а решта — стандартні. Навмання з ящика береться одна деталь. Яка ймовірність того, що вона буде стандартною?

Розв'язання. Число всіх рівноможливих елементарних подій для цього експерименту: =15.

Нехай А — подія, що полягає в появі стандартної деталі. Число елементарних подій, що сприяють появі випадкової події А, дорівнює дев'яти (= 9). Згідно з (2.1) маємо:.