4. Елементи теорії масового обслуговування
Як у сфері виробництва, так і в побуті часто трапляються такі неприємні явища, як черга, що являє собою скупчення (яке буває численним) об'єктів (вимог), які чекають свого обслуговування. Під обслуговуванням об'єкта (вимоги) розуміють виконання стосовно нього (неї) певного комплексу операцій.
Черга може мати місце у повсякденному житті: у магазинах до кас чи до продавця, у поліклініці до лікаря. У виробничій практиці вона виникає під час виробничих процесів, коли накопичуються деталі, вузли, агрегати, які потребують обслуговування робітником, верстатом-автоматом. У більш складних системах обслуговування черги виникають під час навантажування чи розвантажування вагонів, річних та морських суден у портах, обслуговування літаків в аеропортах тощо. Причини, які призводять до черг як у сфері виробництва, так і в сфері обслуговування, мають випадковий характер і виникають тоді, коли:
пропускна здатність «приладу» обслуговування (робітник, касир, верстат-автомат) не задовольняє число вимог, що надходять;
об'єкти (вимоги) надходять нерегулярно, тобто у випадкові моменти часу, утворюючи при цьому пуассонівський потік;
час обслуговування об'єкта (вимоги) не є сталою величиною, а випадковою, і припускається, що вона має експоненціальний закон розподілу ймовірностей.
Математичною моделлю для найпростішої системи масового обслуговування з одним пуассонівським потоком і одним каналом обслуговування (одноканальний прилад), час якого має експоненціальний закон розподілу ймовірностей, є система рівнянь (9.1).
Розв’язуючи систему (9.1) послідовно, отримаємо:
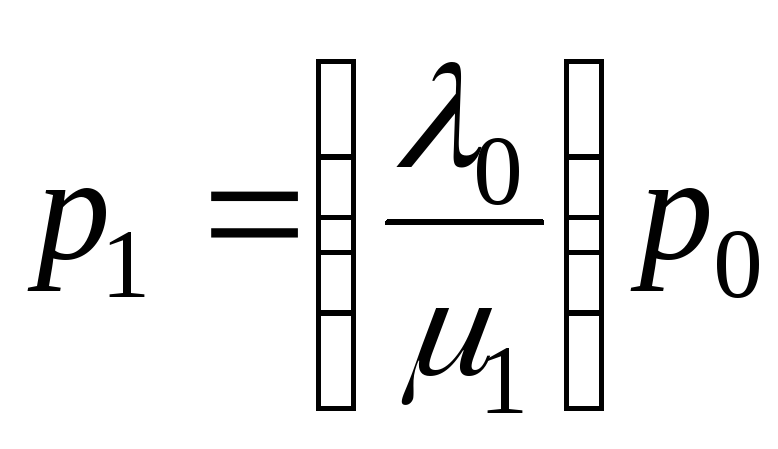, (9.2)
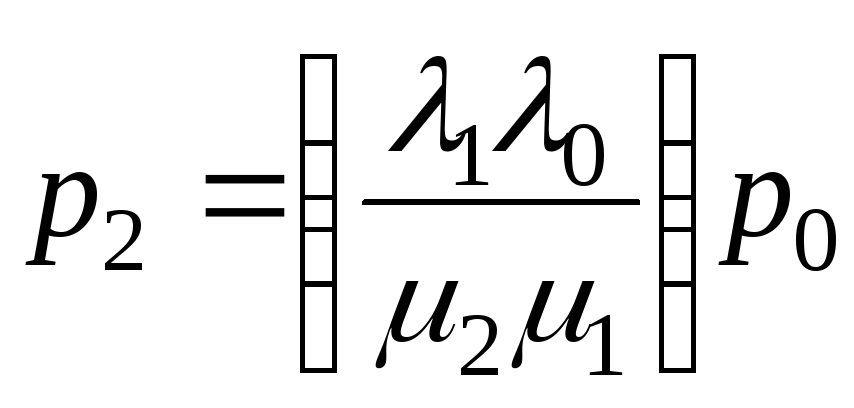, (9.3)
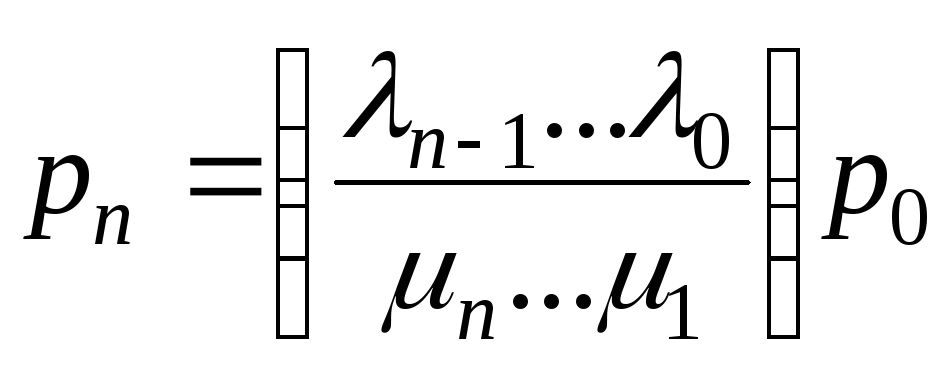. (9.4)
Значення
знаходиться з рівняння: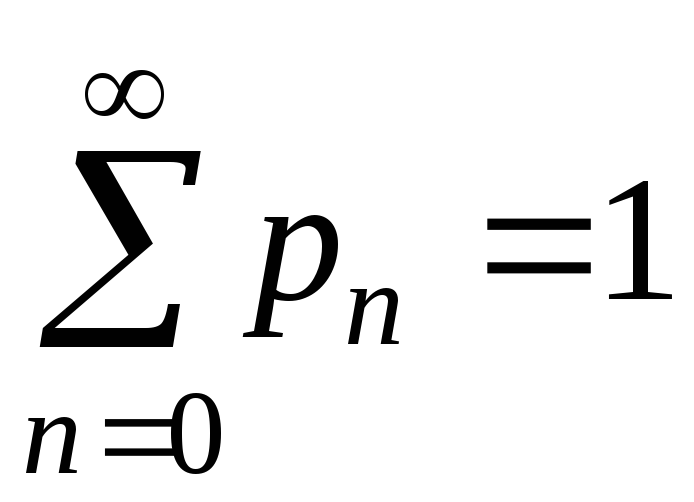
.
Питання для самоконтролю
Що називають випадковим процесом? Їх класифікація.
Що називають реалізацією, випадкового процесу?
Що називають випадкового процесу?
Що називають функцією розподілу перерізу?
Функція розподілу двох перерізів.
Математичне сподівання перерізу випадкового процесу.
Література
Обов’язкова: [1]. Додаткова:[1], [4], [7].
Змістовий модуль 2. Математична статистика
Тема 10. Первинне опрацювання статистичних даних
Мета роботи: з’ясувати основні задачі математичної статистики, її методи, поняття вибіркової сукупності.
План вивчення теми
Предмет математичної статистики.
Генеральна та вибіркова сукупності.
Методичні рекомендації до самостійної роботи
1. Предмет математичної статистики
Мета кожного наукового дослідження - виявлення закономірностей явищ, які спостерігають, та використання цих закономірностей у повсякденній практичній діяльності. Для встановлення цих закономірностей проводять спеціальні досліди та спостерігають одиничні явища. Далі роблять узагальнений висновок у вигляді закону.
У тих випадках, коли явище знаходиться під дією багатьох факторів і неможливо виявити вплив усіх цих факторів, застосовують інший метод вивчення - статистичний, тобто систематизація та обробка статистичних даних однорідних дослідів.
Звичайним є використання статистичних методів в економіці, соціології, політології.
Нехай, наприклад, темп приросту промислового виробництва за певний період часу дорівнює 5%. Це означає, що в середньому для усієї сукупності підприємств показник 5% є статистичною закономірністю зростання промислового виробництва. Цей середній показник не виключає, а, навпаки, припускає, що на окремих підприємствах темп приросту може бути більше або менше 5%.
Предмет математичної статистики полягає в розробці методів збору та обробки статистичних даних для одержання наукових та практичних висновків.
Вкажемо основні задачі, які розв'язує математична статистика:
вказати способи збору та групування (якщо даних дуже багато) статистичних відомостей;
визначити закон розподілу випадкової величини або системи випадкових величин за статистичними даними;
визначити невідомі параметри розподілу;
перевірити правдоподібність припущень про закон розподілу випадкової величини, про форму зв'язку між випадковими величинами або про значення параметра, який оцінюють.
Можна сказати, що основна задача математичної статистики– розробка методів аналізу статистичних даних в залежності від мети дослідження.
Методи математичної статистики ефективно використовують при розв'язанні багатьох задач науки, організації технологічного процесу, планування, управління та ціноутворення.