Задачі для розв’язання

1. Закон розподілу дискретної випадкової величини Х задано таблицею:

Хі	-4	-2	-1	1	2	4
Рі	0,1	0,2	0,1	0,1	0,2	0,3

Побудувати закон розподілу ймовірностей для Y=3Х².

2. За заданим законом розподілу:

Хі	-π/3	-π/4	-π/6	0	π/6	π/4	Π/3
Рі	0,1	0,2	0,1	0,1	0,2	0,1	0,2

Обчислити M(Y), D(Y), ( Y ), якщо Y=cos² Х.

3. Випадкова величина Х рівномірно розподілена в інтервалі (-1, 1). Знайти щільність імовірності випадкової величини Y=Х².

4. Задані розподіли незалежних випадкових величин Х та Y:

Х	-1	0	1
Р(Х)	0,3	0,5	0,2

Y	0	1
Р(Y)	0,4	0,6

Знайти математичне сподівання та дисперсію випадкової величини Z=X²·Y³.

5. Випадкова величина Х розподілена рівномірно в інтервалі (0, 2). Знайти дисперсію випадкової величини Y=3-2Х.

6. Задані розподіли випадкових величин Х та Y:

Х	3	5	7
Р(Х)	0,3	0,5	0,2

Y	2	6
Р(Y)	0,6	0,4

Скласти розподіл величини Z=X+Y та знайти її математичне сподівання .

7. Незалежні випадкові величини Х та Y мають щільності ймовірностей:

f(x) f(y)

-2 x 2 y

Визначити 1) M(2X+3Y-2), D(2X+3Y-2),

2) M(XY), D(XY).

Т е с т и

Варіант №1

Дискретна випадкова величина задана законом розподілу

Х	1	3	5
Р	0,2	0,5	0,3

Нехай Y=X²+1, тоді

1. М( Х ) дорівнює: а) 2,02; б) -1,3; в) 3,2 г) 0.

2. М(Y) дорівнює: а) 11; б) -1,4; в) 4,5 г) 13,2.

3. М(Y²) дорівнює: а) 0,55; б) 123; в) 253,6; г) 134.

4. D(Y) дорівнює: а) 4,5; б) 79,36; в) 2,3; г) 0,14.

Варіант №2

Випадкова величина Х рівномірно розподілена в інтервалі (-1; 1). Для випадкової величини Y=Х² знайти:

1. щільність імовірності;

2. М(Y). а) 1/3; б) -1; в) 1/6 г) 0.

3. М(Y²). а) 45; б) 8,19; в) 5; г) 0,1.

4. D(Y). а) 13/180; б) 14/180; в) 1,1 г) 7,35.

Література

Обов’язкова: [1]. Додаткова:[1], [4], [7].

Практичне заняття №10

Тема 8. Граничні теореми теорії ймовірностей

Мета заняття: Закріпити теоретичні знання і набути практичні навички використання закону великих чисел та граничних теорем в ході розв’язання практичних задач.

Обладнання: 1. Методичні рекомендації і завдання до практичних занять; 2. Мікрокалькулятори.

План заняття

1. Основні теоретичні відомості з теми заняття.

2. Розв’язування задач.

3. Підведення підсумків заняття.

Методичні рекомендації

Нерівність Чебишова. Якщо випадкова величина має обмежені математичне сподівання і дисперсію, то для довільногоε>0 має місце нерівність

.

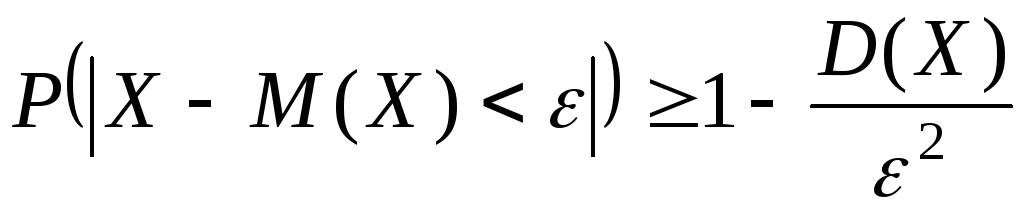Теорема Чебишова. Нехай задано попарно незалежних випадкових величин(, які задовольняють умовам

1) =a_i, 2) D(X_i) ≤C, (C – деяка стала, C>0) ∀ і=1,2,...,n.

Тоді

.

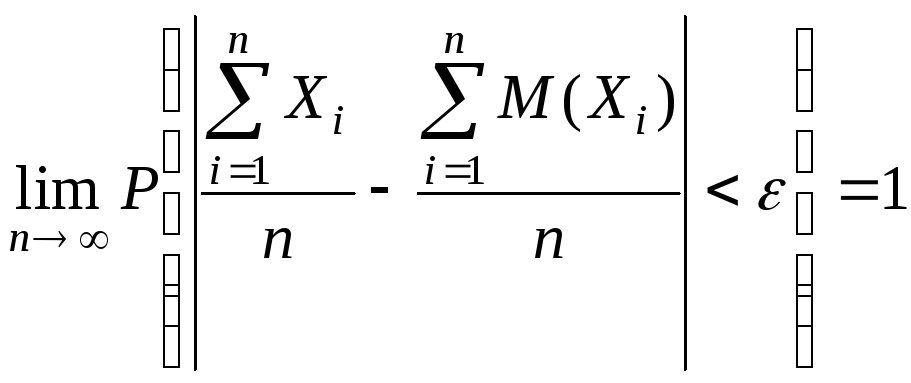Центральна гранична теорема. Нехай задано незалежних випадкових величин(, кожна із яких має один і той самий закон розподілу ймовірностей із,і при цьому існує за абсолютною величиною початковий момент третього порядку, тоді зі зростанням числазакон розподілунаближається до нормального.

Задачі для розв’язання

1. Дисперсія випадкової величини Х дорівнює 0,001. Яка ймовірність того, що випадкова величина Х відрізняється від її математичного сподівання більше ніж на 0,1?

2. Випадкова величина Х має закон розподілу N(-2;4). Скориставшись нерівністю Чебишова, оцінити ймовірність , якщоε=4σ.

3. Випадкова величина Х має такий закон розподілу:

Х	1	5
Р(Х)	0,7	0,3

Використовуючи нерівність Чебишова оцінити ймовірність того, що .

4. Дисперсія кожної із 4500 незалежних випадкових величин, що мають один і той самий закон розподілу ймовірностей, дорівнює 5. Оцінити ймовірність того, що відхилення середнього арифметичного їх математичних сподівань, взяте за абсолютною величиною, не перевищить 0,4.

5. Імовірність виготовити стандартну деталь робітником дорівнює 0,95. Контролю підлягає 400 деталей. Оцінити ймовірність відхилення відносної частоти появи стандартної деталі W(A) від імовірності 0,95 не більше ніж на величину 0,02.

6. Кожна із 100 незалежних випадкових величин має рівномірний закон розподілу на проміжку [0; 0,12]. Записати наближено закон розподілу для випадкової величини .

7. Із якою надійністю середнє арифметичне вимірів певної величини відповідає істинному виміру цієї величини, якщо було здійснено 500 вимірювань із точністю 0,1 і при цьому дисперсії випадкових величин – результатів вимірювання – не перевищують 0,3.

8. Скільки необхідно провести вимірів діаметра втулки, щоб середнє арифметичне цих вимірів відрізнялося від істинного розміру діаметра втулки не більше як 0,05 із надійністю 90%, якщо дисперсії випадкових величин (результатів вимірів) не перевищують 0,2.

9. Випадкова величина – середнє арифметичне 10000 незалежних випадкових величин , що мають один і той самий закон розподілу, і середнє квадратичне відхилення кожної із них дорівнює 2. Яке максимальне відхилення величинивід його математичного сподівання можна очікувати з імовірністю 0,9544?

10. Верстат із програмним управлінням виготовляє за робочу зміну 900 виробів, із яких в середньому 1% складає брак. Знайти наближено ймовірність того, що за зміну буде виготовлено не менше 810 доброякісних виробів, якщо вони виявляються доброякісними незалежно один від одного.