5. Умовна ймовірність

5.1. Залежні та незалежні випадкові події

Випадкові події А і В називають залежними, якщо поява однієї з них (А або В) впливає на ймовірність появи іншої. У противному разі випадкові події А і В називаються незалежними.

Приклад 1. В урні міститься 10 однакових кульок, із них 6 чорних і 4 білих. З урни навмання беруть дві кульки по одній без повернення. З'ясувати, чи будуть залежними такі події: перша кулька виявиться чорною і друга також.

Розв'язання. Позначимо через А появу чорної кульки при першому вийманні, а через В — при другому. Випадкові події А і В будуть залежними, оскільки поява чорної кульки при першому її вийманні з урни (випадкова подія А) впливатиме на ймовірність появи чорної кульки (випадкова подія В) при другому вийманні.

Приклад 2. З урни, де шість білих і чотири чорні кульки, вийняли дві кульки по одній, при цьому перша кулька в урну повертається.

З'ясувати, чи будуть залежними такі події: перша виявиться чорною, друга також.

Розв'язання. Нехай А — поява чорної кульки при першому вийманні, а В — при другому. Поява чорної кульки при першому вийманні (здійснилась подія А) не впливатиме на ймовірність появи чорної кульки (подія В) при другому вийманні, оскільки співвідношення між чорними та білими кульками в цьому разі не змінюється.

5.2. Обчислення умовної ймовірності

Якщо ймовірність випадкової події А обчислюється за умови, що подія В відбулася, то така ймовірність називається умовною. Ця ймовірність обчислюється за формулою

. (2.7)

6. Формули ймовірностей добутку та суми випадкових подій

Згідно із (2.7) маємо:

. (2.8)

Формула (2.8) має місце в загальному випадку. Якщо події А і В є незалежними то, за означенням, . Для незалежних подій з (2.8) випливає:

. (2.9)

Імовірність суми двох несумісних поді А і В є:

. (2.10)

Імовірність суми двох сумісних поді А і В є:

. (2.11)

7. Імовірність появи хоча б однієї випадкової події

Нехай є n сумісних випадкових подій ,,...,. Позначимо черезподію, яка полягає в тому, що з'явиться хоча б одна з цих подій. Тоді подіяце подія за якої жодна з подій не відбудеться. Подіявизначається як. Подіїтаутворюють повну групу подій, тому

.

Звідси одержуємо

(2.12)

За цією формулою треба обчислювати імовірність появи хоча б однієї випадкової події з n сумісних подій.

1320 11

8. Формула повної ймовірності

У разі, коли випадкова подія А може відбутися лише за умови, що відбудеться одна з несумісних випадкових подій ,, ..., які утворюють повну групу і між собою є попарно несумісними, імовірність події А обчислюється за формулою:

. (2.13)

Яка називається формулою повної ймовірності.

Випадкові події ,, ...називаютьгіпотезами.

9. Формула Байєса

Нехай в умовах задачі, що відноситься до формули повної ймовірності, провели одну спробу експерименту, в результаті якої відбулася подія А. Запитується: як змінилися (у зв'язку з тим, що подія А уже відбулася) імовірності гіпотез, тобто величини , k = 1,....,n ?

Знайдемо умовну імовірність . За теоремою добутку ймовірностеймаємо:

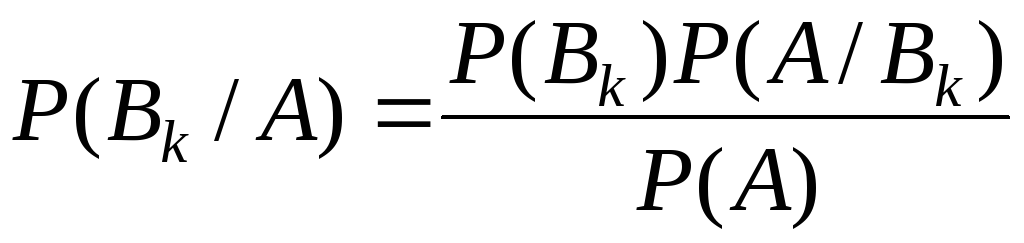, (2.14)

де обчислюється за формулою (2.13).

Формула (2.14) називається формулою Байєса (Томас Байєс, чи Бейєс (1702 – 1761), - англійський математик).

Питання для самоконтролю

1. В якому разі P(A/B) = 1?

2. Формула добутку ймовірностей для двох залежних випадкових подій А і В.

3. Чому дорівнює P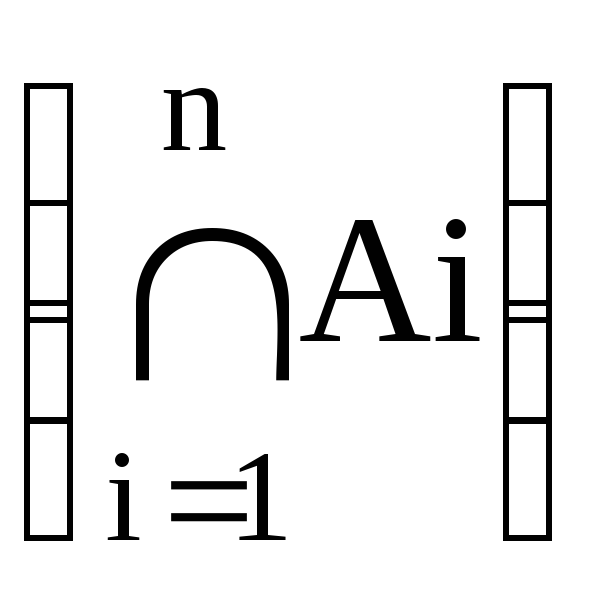, якщо випадкові подіїА_i є залежними?

4. Чому дорівнює Р (A∩B) , якщо А і В є незалежними?

5. В якому разі P(A/B) = P(A), P(B/A) = P(B)?

6. Формула для обчислення появи випадкової події хоча б один раз при n незалежних експериментах має вигляд...

7. Гіпотези у формулі повної ймовірності та їх властивості.

8. Формула повної ймовірності випадкової події А за наявності n гіпотез B_i.

9. В якому разі використовується формула Байєса?

10. В якому разі обирається гіпотеза B_i для прийняття рішення при проведенні експерименту?