Задачі для розв’язання
1. За заданим законом розподілу ймовірностей
1
0,9
0,8
0,7
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
xi
0
F
0,6
0,55
0,4
0,3
0,2
0,1
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
xi
0
ni
0,149
0,069
0,046
0,023
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
0
ni
6
5
4 3
2
1
xi f(x) F(x) 1 x
8 1
x
1
Хі
-6
-4
1
3
5
8
Рі
0,1
0,2
0,1
0,2
0,2
0,2
F(x)
1
обчислити M(X), D(X), (X).
2. Нехай Х – число гербів, що випали при підкиданні двох симетричних монет. Записати закон розподілу випадкової величини Х. Обчислити M(X), D(X)
3. Задано функцію розподілу ймовірностей випадкової величини Х:
.
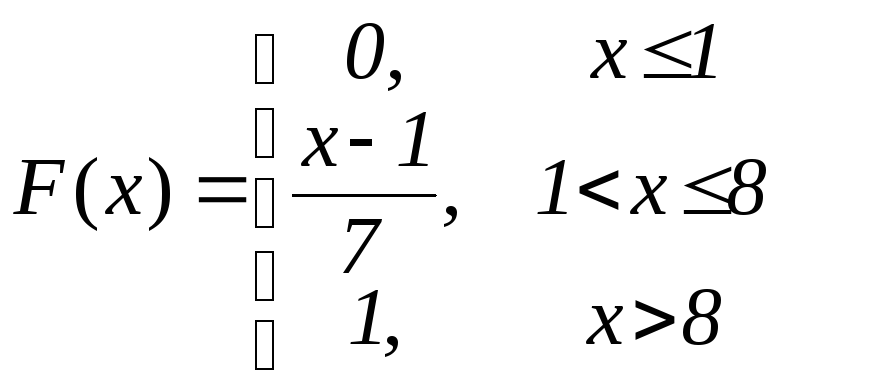Знайти M(x). Обчислити Р(2<Х<3,5).
4. Знайти математичне сподівання і дисперсію кількості очок, що з’являться в результаті одного підкидання грального кубика.
5. За заданою щільністю ймовірностей
f(x)=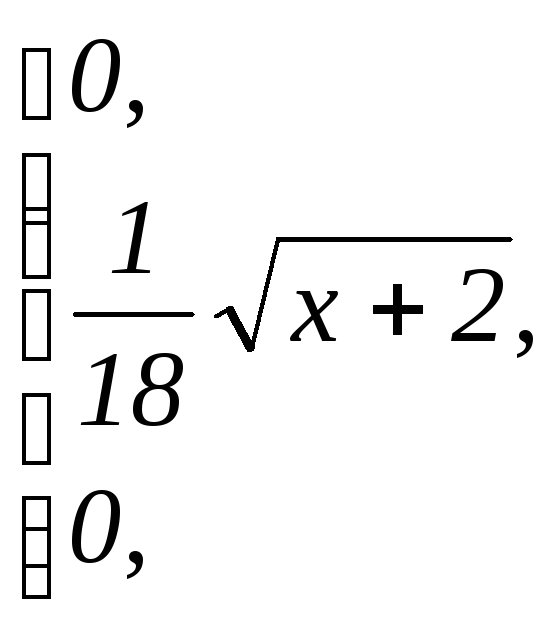
обчислити M(x).
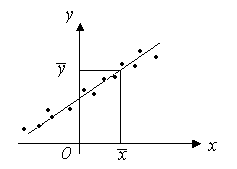
6. Графік щільності розподілу імовірності зображено на рисунку.
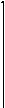f(x)
1/3
-2
-1 1 2 3 4
Знайти аналітичний вираз щільності розподілу. Обчислити D(X), (X), Мо, Ме.
7. Знайти математичне сподівання випадкової величини з а) біноміальним розподілом, б) розподілом Пуассона, в) рівномірним розподілом.
8. По мішені проведено 9 пострілів. Імовірність влучення у мішень при кожному пострілі дорівнює 0,7. Знайти математичне сподівання і дисперсію числа влучень.
9. Випадкова величина Х розподілена за нормальним законом з математичним сподіванням 40 і дисперсією 200. Обчислити ймовірність влучення Х в інтервал (30,80).
10. Випадкова величина Т – час роботи приладу має показниковий розподіл. Визначити ймовірність того, що час роботи приладу буде не менше 600 годин, якщо середній час роботи становить 400 годин.
Т е с т и
Варіант №1
1. Знайти математичне сподівання числа очок, які можуть з’явитися при підкиданні грального кубика.
а) 3; б) 1/2; в) 7/2; г) 5/2.
2. Випадкова величина Х задана щільністю імовірності:
Визначити дисперсію величини Х.
а) 1/2; б) 2/3; в) 2/9; г) -2/3
3. Випадкова величина розподілена за показниковим законом з параметром 5. Знайти М( Х ) і D( Х ).
а) М( Х )=5 D( Х )=25; б) М( Х )=0,2 D( Х )=0,2;
в) М( Х )=0,2 D( Х )=0,04; г) М( Х )=0,5 D( Х )=0,5.
4. Який з наступних законів розподілу не відноситься до розподілу дискретних випадкових величин?
а) рівномірний;
б) пуассонівський;
в) геометричний;
г) біноміальний.
5.
Випадкова величина Х розподілена за
законом
.
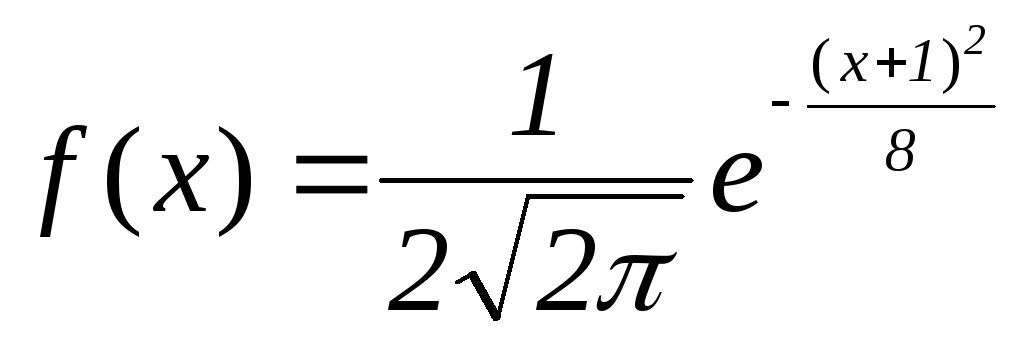Знайти М( Х
) і (
Х
).
а) М( Х )=2 ( Х )=2; б) М( Х )=-1 ( Х )=2;
в) М( Х )=8 ( Х )=4; г) М( Х )=-2 ( Х )=1.
Варіант №2
1. Знайти дисперсію випадкової величини Х, що задана законом
|
Х |
-5 |
0 |
4 |
5 |
|
Р |
1/8 |
1/2 |
1/4 |
1/8 |
а) 86/8; б) –74/8; в) 1; г) 74/8.
2. Задана інтегральна функція
F(x)=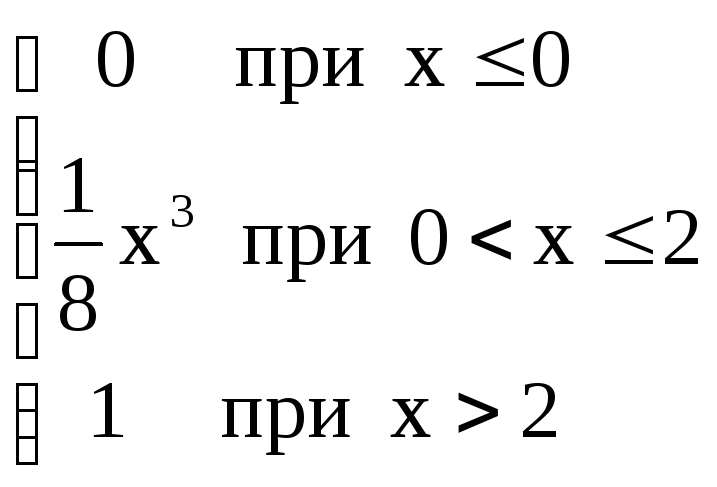
;
M(X) дорівнює: а) 1/2; б) 7/8; в) 7/8; г) 3/2.
3. Випадкова величина розподілена рівномірно в інтервалі (-2;2).
Знайти М( Х ) і D( Х ).
а) М( Х )=0 D( Х )=1,33; б) немає вірної відповіді;
в) М( Х )=0 D( Х )=4; г) М( Х )=0,5 D( Х )=1,25.
4.
За яких умов ймовірність влучення
випадкової величини Х
в інтервал (c, d) знаходять за формулою:
.
а) Х має рівномірний розподіл;
б) Х має показниковий розподіл;
в) Х має нормальний розподіл;
г) Х має біноміальний розподіл.
5. Випадкова величина Х має показників розподіл з параметром 3. Знайти імовірність того, що Х потрапить в інтервал (0,13; 0,7).
а) 0,555; б) 1; в) 0,34 г) 0,445.