Т е с т и

Варіант №1

1.Умовою нормування для неперервних випадкових величин є:

а) ; б); в); г).

2. В яких межах лежить коефіцієнт кореляції?

а) від 0 до 1; б) від - до ; в) від - до ; г) від –1 до 1.

3. Закон розподілу системи двох випадкових величин Х і Y має вигляд:

Y Х	0	1
0	0,2	0,15
1	0,15	0,15
2	0,1	0,25

Знайти D(Y).

а) 0,2; б) 1; в) –1; г) 0,7.

4. Задано двовимірний закон розподілу:

Y X	1	2	3
-1	0,2	0,1	0,3
0	0,15	0,15	0,1

Обчислити М(X /Y =-1).

а) 13/6; б) 12/6; в) 2/3 г) 0.

5. По мішені проводиться один постріл. Ймовірність влучення дорівнює p. Розглядається Х – кількість влучень, Y – кількість промахів. Побудувати розподіл ймовірностей системи випадкових величин (Х, Y).

Варіант №2

1. Яке з наведених тверджень невірне?

а) 0F(x)1; б) якщо r_xy=0, то Х і Y незалежні; в)r_xy1; г) всі вірні.

2. Якщо К_xy=0, то чому дорівнює r_xy?

а) -2; б) ; в) 1; г) 0.

3. Закон розподілу системи двох випадкових величин Х і Y має вигляд:

Y X	0	1
0	0,2	0,15
1	0,15	0,15
2	0,1	0,25

Знайти М( Х ) і М(Y).

а) М( Х )=1,2 М(Y)=4,3; б) М( Х )=2,6 М(Y)=0,4;

в) М( Х )=0,55 М(Y)=1; г) М( Х )=1 М(Y)=1.

4. Задано двовимірний закон розподілу:

Y X	1	2	3
-1	0,2	0,1	0,3
0	0,15	0,15	0,1

Обчислити D(Y/X =3).

а) 3/6; б) 3/16; в) 2/4 г) 9/4.

5. Ймовірність того, що при перевірці деталь виявиться стандартною, дорівнює 0,7. Перевірці підлягають 2 деталі. Побудувати закон розподілу системи двох дискретних випадкових величин Х – появи числа бракованих деталей і Y – появи числа стандартних деталей.

Література

Обов’язкова: [1]. Додаткова:[1], [4], [7].

Практичне заняття №9

Тема 7. Функції випадкового аргументу

Мета заняття: Закріпити теоретичні знання і набути практичні навички розрахунку числових характеристик функції дискретного та неперервного випадкових аргументів в ході розв’язання практичних задач.

Обладнання: 1. Методичні рекомендації і завдання до практичних занять; 2. Мікрокалькулятори.

План заняття

1. Основні теоретичні відомості з теми заняття.

2. Розв’язування задач.

3. Підведення підсумків заняття.

Методичні рекомендації

Якщо вказано закон, за яким кожному можливому значенню випадкової величини X відповідає певне значення випадкової величини Y, то Y звуть функцією X і позначають .

Нехай – функція випадкового аргументу. Якщо X - дискретна випадкова величина, то Y також дискретна випадкова величина із відповідними значеннями.

Математичне сподівання, дисперсію та середнє квадратичне відхилення функції Y обчислюють за формулами:

,

,

.

Коли X — неперервна випадкова величина, закон розподілу якої заданий щільністю ймовірностей, і – диференційовна функція, монотонна на усьому проміжку можливих значень X, то щільність розподілу функції визначають так

.

де - функція, обернена по відношенню до функції .

Числові характеристики функцій неперервного випадкового аргументу визначаються за формулами:

; ;

.
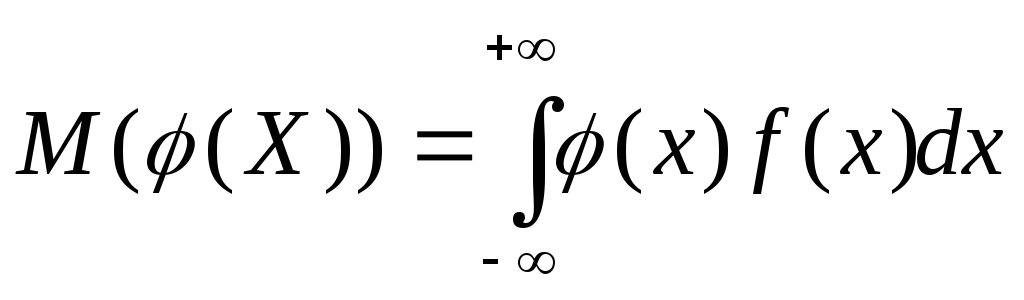
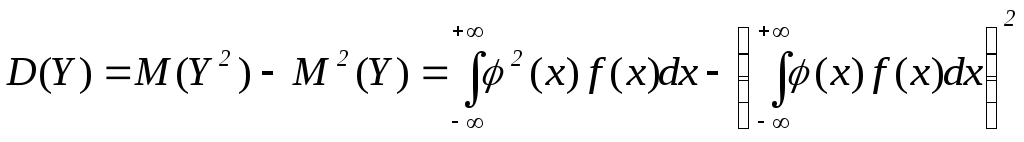