
Кобрунов А_Мат методы модел в прикл геоф 2
.pdf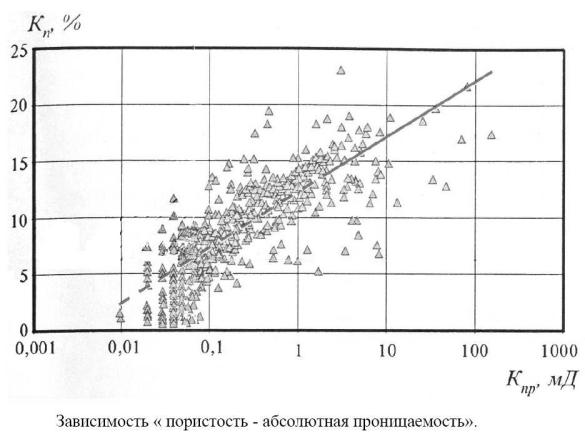
Рисунок 1.25 – Характер распределения исходных данных
Поскольку нечеткие отношения представляют собой также нечеткое множество, но с большей размерностью универсума, между ними может быть определены правила оперирования
отношениями как нечеткими множествами. |
|
|
|
|
|
|
|
|
||||||
Пусть |
имеется |
два |
нечетких |
отношения |
A и M , |
определенные на N мерном |
||||||||
универсуме |
X Xi , i 1,..N |
|
с |
функциями |
принадлежности |
A x1 , x2 ,...xN и |
||||||||
M x1 , x2 ,...xN соответственно. |
|
|
|
|
|
|
|
|
|
|
|
|||
Пересечением нечетких отношений A и M A M |
называется новое отношение S с |
|||||||||||||
функцией принадлежности |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
S x1 , x2 ,...xN min{ A x1 , x2 ,...xN , M x1 , x2 ,...xN } |
|||||||||||||
|
S 1 |
2 |
N |
|
A 1 2 |
|
N |
|
M |
1 |
2 |
N |
. |
|
|
|
x , x ,...x |
|
|
x , x ,...x |
|
|
|
x , x ,...x |
|
} |
|||
Объединением нечетких отношений A и M A M |
называется новое отношение S с |
|||||||||||||
функцией принадлежности |
|
|
|
|
|
|
|
|
|
|
|
|
||
191




