
Кобрунов А_Мат методы модел в прикл геоф 2
.pdf
1.2.5 Принцип оптимальности Беллмана
Приведем некоторые типичные задачи, возникающих в геофизических методах и
имеющих смысл нахождения наилучшей траектории, выходящей из заданной точки x0 и
заканчивающейся в точке xend .
Первая задача это корреляция границы между системой скважинами с использованием фрагментов отражений на временном разрезе. Надо найти такой путь, чтобы он имел наименьшее число изгибов, проходя через фиксированные реперы, и имел, например,
минимальную длину захватывая как можно больше участков регулярных компонент волнового поля. Это задача нахождения корреляции разрезов сведенная к нахождению оптимальной
траектории. Траектория описывается кривой s параметр. Имеется критерий
который оценивает оптимальность участка траектории соответствующего значению параметра s
от 0 до величины равной s . Траектория заканчивается при значении параметра s send . Строго говоря, необходимо решить задачу:
J x send min, x 0 x0 .
Если критерий оптимальности допускает аналитическое представление в виде
дифференцируемого функционала, то ее решение сводится к построению уравнения Эйлера для этой задачи и последующего его анализа и решения. Но уже в простейших случаях построение уравнения Эйлера оказывается не самым эффективным приемом.
Другой пример это движение точки вдоль траектории в поле скоростей V x, y, z
подчиняющееся принципу Ферма – время движения из начальной в конечную точку должно быть минимальным. Это приводит к задаче:
end
dl
0 V x s min ,
где dl – дифференциал длинны дуги кривой x s . Последнее выражение переписывается:
|
|
dx s 2 |
|
||
s |
1 |
|
|
|
|
ds |
|
||||
end |
|
|
|
|
|
|
|
|
|
|
min . |
|
V x s |
|
|||
0 |
|
|
|
||
121
По сути это задача расчета траектории луча в задачах сейсморазведки и сейсмологии.
В практически значимых ситуациях функция скорости достаточно сложна и уравнение Эйлера для нее достаточно сложно разрешимо. Дело становиться почти безнадежным, если функция скорости – клеточно задана своими значениями. Здесь прямые вычисления на основе уравнения Эйлера или перебор значений с целью сравнения вариантов и поиска наилучшего приводят к грандиозным размерам вычислений.
Еще один типичный пример – это задача корреляции временных разрезов в сейсморазведке, которая моделирует более общую задачу корреляции приведенную в первом примере
Приведенные примеры иллюстрируют общую задачу динамического программирования,
состоящую в нахождении оптимальной траектории, каждый фрагмент которой сам по себе есть оптимальная траектория.
Общий алгоритм ее решения, называемый принципом Беллмана, проиллюстрируем на примере решения частной задачи.
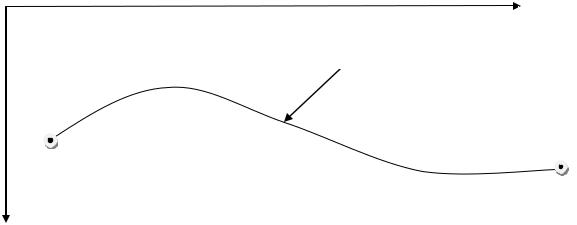
Рассматривается алгоритм решения двухточечной задачи оптимизации, состоящей в нахождении траектории, минимизирующей заданный функционал (рис. 1.1):
|
|
l d |
|
|
|
|
||
min |
|
|
|
r r |
. |
|||
3к |
||||||||
L r0,r |
|
|
0, |
|
||||
L r0,r |
|
|
|
|
|
|
||
L x0 , x
x0
Y
Рисунок 1.9 – Двухточечная задача оптимизации
(1.2.35)
X
x
Двухточечной она называется, потому что две точки – начало и конец траектории,
закреплены и известны. Это точки x0 и x ,
Задача (1.2.35) выражает аналог принципа Ферма, записанного с использованием минимизации интеграла, играющего роль интеграла Ферма для движения точки перегиба кривой
122

изменения давления во времени. Отличительной чертой (1.2.35) от стандартной, записанной выше двухточечной задачи поиска оптимальной траектории, обеспечивающей минимальное время движения, служит вхождение самой этой траектории под интеграл или, что то же самое,
зависимость «скорости движения луча» V 3к от длинны пройденного пути. Скорость
l
убывает пропорционально длине пройденного «лучом» пути и это приводит к существенным изменениям кинематики движения. Таких модификаций и аналогов минимизируемого функционала может быть много. Конкретно задача (1.2.35) более общая, чем стандартная модель поиска траектории с минимальным временем с заранее заданной скоростью движения. Именно на этом примере и рассмотрим основные принципы Беллмановского алгоритма для решения задачи.
Переходим к дискретной сети: направив ось индекса i вправо, как дискретного аналога переменной X , ось индекса j вниз, как дискретного аналога переменной Y (рис. 1.10)
X
L x0 , x 


 x
x
x0
Y 
Рисунок 1.10 – Дискретная модель задачи оптимизации
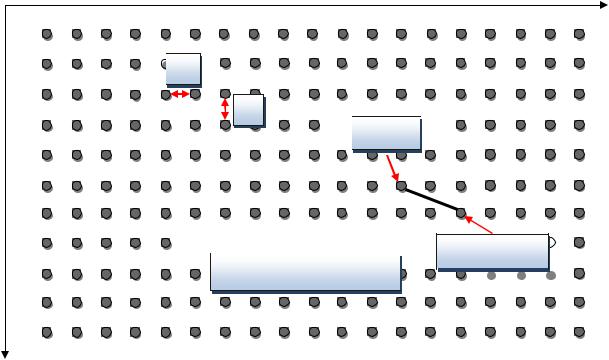
Для простоты можно считать, что сеть прямоугольная с размером N M и интервал между точками равен x и y соответственно. Сети соответствует дискретный набор точек –
узлов сети имеющих координатное x, y и двух индексное i, j представление i, j .
Начальная пара индексов 1, n характеризует начальную точку x0 1, n . Конечная точка
x N, m .
123
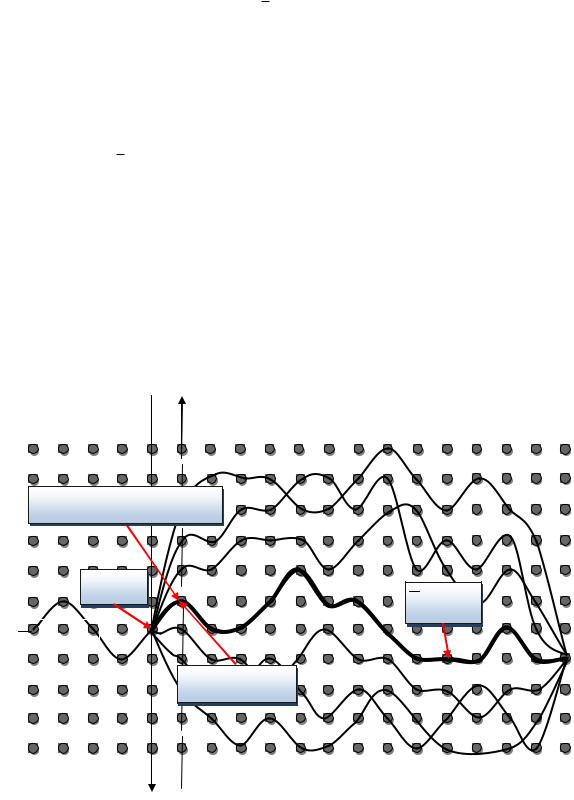
Пусть искомая траектория L x0 , x в своем дискретном представлении (обведено
жирным) имеет вид последовательности 1, n , которая имеет последовательность индексов
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
. Каждый ее фрагмент это интервал |
i, j |
i |
, |
i 1, j |
, соединяющий узлы |
|||||||||||
i, j |
|
|
|
|
|
|
|
i 1 |
|||||||||
i, j i |
и i 1, j i 1 (рис. 1.11). |
|
|
|
|
|
|
|
|
|
|
|
|||||
Пусть i, j произвольный узел сети (рис. 1.12), фиксирующий точку i, j .
Обозначим i, j последовательность, реализующую на задачи:
|
|
l d |
i, j , x . |
||
min |
|
|
|||
3к |
|||||
L i, j ,x |
|
|
|
||
L i, j ,x |
|
|
|
||
дискретной сети решение
(1.2.36)
Это оптимальная последовательность, начатая из точки (i, j) и завершенная в
x m, N .
i, j i , i 1, j i 1
j i 1
i, j i |
i, j i |
|
|
1, n |
|
|
i 1, j i 1 |
Рисунок 1.11 – Дискретная модель
124
 X
X
 Y
Y

 i, j i
i, j i 



 i 1, j i 1
i 1, j i 1  i, j i , i 1, j i 1
i, j i , i 1, j i 1 

Рисунок 1.12 – Пояснение к обозначениям
Задача (1.2.36) существенно отличается от (1.2.35) тем, что в (1.2.36) используется лишь часть общей длинны пройденного пути в то время как при расчете вклада того же сегмента в
(1.2.35) учитывается весь путь пройденный в том числе и до точки i, j . Таким образом,
каждый узел l, k имеет продолжение по оптимальности до конечной точки x m, N
начало l, k может быть произвольным из диапазона допустимых индексов. Для каждой точки
i, j |
имеется |
ее |
|
продолжение |
на |
|
i 1,...N -образующее. |
|
|
Так |
|
что |
в предположении |
||||||||||||||||||||||||||
единственности решения задачи (1.2.36) из каждой |
|
точки |
i, j |
исходит |
ровно |
одна |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
i, j , |
соединяющая i, |
j |
|
и r s N, m . |
|
|||||||||||||||||||||||||||||
оптимальная траектория |
|
При фиксированном i |
|||||||||||||||||||||||||||||||||||||
таких траекторий ровно M по числу значений индекса |
|
j . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
i, j |
|
|
|
индексами i, j i |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
Линия |
|
|
|
определенная |
|
состоит |
|
из |
суммы |
фрагментов: |
||||||||||||||||||||||||||
|
|
|
|
|
i 1, j i 1 : |
|
|
i 1, |
|
j i 1 |
|
||||||||||||||||||||||||||||
последовательности, |
исходящей |
из |
узла |
|
|
и элемента, |
|||||||||||||||||||||||||||||||||
соединяющего |
i, j |
|
i |
и |
i 1, j |
|
i 1 |
|
|
|
i, j |
|
i |
|
, i 1, j |
|
i 1 |
. |
Считая, |
что |
|||||||||||||||||||
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
i 1, j |
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, i 1, j |
|
i 1 |
|
|
|
|
||||||||||||
|
задано, оптимальный участок |
|
i, j |
i |
|
соединяющий точки |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
125
|
|
|
|
|
|
|
|
i 1, j i 1 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
i, j i и i 1, j i 1 и наращивающий |
до i, j обеспечивает решение |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
задачи (рис. 1.11): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
J |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
min J |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. (1.2.37) |
||||||||||||||||
|
i, j |
|
i |
, i 1, j |
|
|
i 1 |
|
|
|
|
i 1, j |
|
i |
1 |
|
|
i, j |
|
|
i |
, |
|
i |
1, k |
|
|
|
i 1, k |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сумма фрагментов понимается в смысле их композиции – продолжения одного фрагмента |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
другим так, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
i, j |
|
i |
, |
|
i 1, j |
|
i |
1 |
|
|
|
|
|
|
i |
1, j |
|
|
i 1 |
|
|
|
|
i, j |
|
i |
|
. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вид функционала J |
|
определен в (1.2.36): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J i, |
j |
|
|
|
|
|
i, j ,x |
3к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.2.38) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
i, |
j численно совпадает с временем движения точки перегиба из узла |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Величина J |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
i, |
j |
в |
r , |
которое в соответствии с (1.2.36) |
|
|
обозначается i, j , r . В условиях задания |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
дискретной сети алгоритм вычисления интеграла (1.2.38) почти очевиден и состоит в следующем.
Пусть i, j i последовательность узлов сетки, определяющую L i, j , r l i, j i , N, m и
l i длина интервала, между точками i, j |
и i 1, j i 1 . Тогда |
|
||||||||||||||
|
|
l |
d |
|
|
|
|
2 l i x |
|
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3к |
|
|
|
3 |
|
|
|
|
|
|
|||||
L i, j , i 1,k |
|
|
|
|
|
|
||||||||||
|
|
|
|
к i, j к i 1, j i 1 |
(1.2.39) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
|
|
|
|
y |
|
|
j i 1 j i |
|
|
|
||||||
l i |
|
|
2 |
|
2 |
|
2 |
|
|
|||||||
x |
|
|
|
. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В соотношении (1.2.39) значение коэффициента |
пьезопроводности к i, j |
на линии |
|
соединяющей узлы i, j i |
и i 1, j i 1 |
принят постоянным и |
равным |
среднеарифметическому между значениями в крайних узлах сетки. |
|
||
Для интеграла (1.2.38) теперь легко построить конструкцию |
|
||
|
|
|
|
|
|
|
l d |
|
N 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
i, j , x J i, j |
|
|
|
|
|
|
|
||
|
|
i, j ,x |
3к |
i |
|||||
|
|
|
|
L |
|
||||
|
|
2 l i x |
|
|
|
|
. |
3 |
|
|
|
к i, j к i 1, j i 1 |
|||
Обозначим:
126

|
|
|
|
|
|
|
|
|
|
|
J |
i, j J |
i, j |
|
; |
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
l d |
|
|
|
|
|
|
|
|
|||
J i, j , i 1, k |
|
i, j , i 1,k |
3к |
||||||
|
|
|
|
|
|
|
|||
Здесь, как и ранее, i, |
j , i 1, k линия, соединяющая между собой точки i, j и |
||||||||
i 1, k .
Справедливо следующее из (1.2.37) утверждение:
|
|
|
|
|
|
|
i, j min J i, |
j , i 1, k |
|
i 1, k . |
|
|
|
|
|
|
|
|
|
(1.2.40) |
|||||||||||||||||||||||||||
|
|
|
|
|
J |
J |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Теперь можно определить следующий численный алгоритм решения задачи (1.2.35). |
|||||||||||||||||||||||||||||||||||||||||||||||
Область S в пространстве |
X Y разбивается сеткой |
N M так, |
что начальная точка |
||||||||||||||||||||||||||||||||||||||||||||
x0 1, n , конечная r N, m . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Шаг 1. Рассчитывается M значений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i, j |
|
i, j |
, |
N, m |
|||||||||||||||
J N 1, j J N 1, j , N, m , j 1 M. i |
N |
1. |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Шаг 2. Для каждого j 1 M решается задача: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
i, j |
min J |
|
i 1, j , i, k |
i, k |
. |
|
|||||||||||||||||||||||||||||||||
|
|
J i 1, j , (i, j |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||
|
|
|
|
i 1, j |
i |
|
|
i 1, j |
i |
, (i, j |
i |
|
|
|
|
|
|
|
i, j |
|
i |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Шаг 3. Рассчитывается M значений
Ji 1, j J i 1, j
;
Шаг 4. i i 1; Если i 1 перейти к 2. В противном случае:
Шаг 5. Рассчитываем M значений
J |
|
|
|
2, j |
|
. |
||
|
||||||||
1, n , (2, j |
|
|||||||
|
|
|
|
|||||
|
j значение |
|
1, j , |
|
||||
Находим минимальное по |
J |
соответствующее значению индекса j . |
||||||
Величина интервального времени распространения возмущения между точками 1, n и N, m
равна
127

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J 1, j . |
(1.2.41) |
|||||||
J 1, n , (2, j |
|
|
|
|
2, j |
|
|
||||
Оптимальная траектория соединяющая 1, n и N, m есть: |
|
||||||||||
|
|
2, j L x0 , x |
|
||||||||
1, n , 2, j |
(1.2.42) |
||||||||||
1.2.6 Основные понятия о нейронных сетях [2]
Нейронные сети – условное название способа нахождения выходных значений некоторой
произвольной системы по входным и настраиваемым параметрам системы. Основной теоретической предпосылкой, лежащей в основе того, что принято называть нейронной сетью служит следующая теорема Фунахаши (Funahashi).
Теорема. Пусть g x x xi ,i 1 n |
непрерывное |
отображение |
замкнутого |
||||||||||||
ограниченного подмножества K из Rn в R . Пусть |
далее |
x строго возрастающая |
|||||||||||||
непрерывная функция из R в R . Тогда, |
для |
любого |
0 , |
найдется целое |
число N и |
||||||||||
вещественные числа i ,i 1 N и ij ,i 1 N, j 1 n такие что: |
|
||||||||||||||
|
g x |
N |
|
|
|
|
|
|
n |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||||
sup |
i f |
|
ij xj |
|
. |
|
|
||||||||
x K |
|
|
i 1 |
|
|
|
|
|
|
j 1 |
|
|
|
(1.2.43) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Последнее условие можно переписать и в эквивалентной форме, если обозначить |
|||||||||||||||
|
g x |
N |
|
|
|
|
|
|
n |
|
|
|
|||
|
i f |
|
ij x j |
: |
|
|
|||||||||
|
|
|
i 1 |
|
|
|
|
|
|
j 1 |
|
|
|
||
|
|
g x g x |
|
|
|
C K . |
|
|
|
(1.2.44) |
|||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Смысл этой теоремы состоит в том, что в области |
K любую непрерывную функцию с |
||||||||||||||
любой наперед заданной точностью можно аппроксимировать выражением: |
|
||||||||||||||
|
|
N |
|
n |
|
|
|
|
|
|
|||||
|
|
i |
|
ij xj . |
|
|
|
(1.2.45) |
|||||||
|
|
i 1 |
|
j 1 |
|
|
|
|
|
|
|||||
Для этого необходимо определить число N и веса i ,i 1 N и ij ,i 1 N, j 1 n .
Процесс такого нахождения называется обучением. Это тоже условное название как и геометрическая интерпретация аппроксимационного соотношения (1.2.45) как некоего
«нейрона». Если внимательно посмотреть на соотношение (1.2.45), то нетрудно заметить, что речь
128
идет об обычной аппроксимации функции f x линейной комбинацией интервальных
n
значений функции f x . Требуемый интервал рассчитывается в члене ij x j . Матричные
j 1
элементы ij ,i 1 N, j 1 n это и есть коэффициенты для расчета новых значений
n |
|
yi ij xj |
для обычной кусочной аппроксимации g x линейной комбинацией функций |
j 1 |
|
yi . Число этих переменных N может быть (и есть на самом деле) меньше чем число
переменных n участвующих в аппроксимируемой функции. Однако удобной оказалась образная интерпретация процесса, моделируемого правилом (1.2.45) как процесса, происходящего в реальных элементах мозга живых существ. Эта же образная интерпретация облегчает манипулирование с рассматриваемыми элементами. Приведем ее.
|
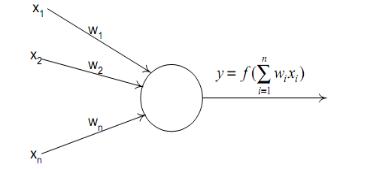
Элементарный нейрон это система, преобразующая вектор x xi ,i 1 n в скаляр y |
||
по правилу: |
|
|
|
1. |
Вычисление скалярного произведения вектора x xi ,i 1 n с вектором (ковектором) |
||
|
весовых коэффициентов W wi ,i 1 n (расчет уровня активации); |
||
2. |
К рассчитанному скалярному произведению применение передаточной функции f . В |
||
|
|
n |
|
|
результате получается скаляр y f |
wi |
xi . |
|
i 1 |
|
|
Рисунок 1.13 – Искусственный нейрон
В качестве функций активации выбираются, например:
|
1 |
|
|
||
|
f |
|
; |
|
|
1 e |
|
||||
|
f |
e e |
; |
||
|
|||||
|
|
|
e e |
|
|
|
f arctg . |
||||
129
Соотношение |
(1.2.45) |
||||
несколько |
|
отличается |
от |
||
|
n |
|
|
|
|
y f wi xi |
|
присутствием |
|||
i 1 |
|
|
|
|
|
еще одного «перемешивающего» |
|||||
|
n |
|
|
|
|
члена |
ij x j |
. Его |
действие |
||
|
j 1 |
|
|
|
|
можно графически представить как |
|||||
последовательность |
|
из |
|||
элементарных |
|
|
нейронов, |
||
образующих слой так, что каждый |
|||||
элемент |
этого |
|
внутреннего |
слоя |
|
принимает последовательность из |
|||||
n значений и образует на выходе
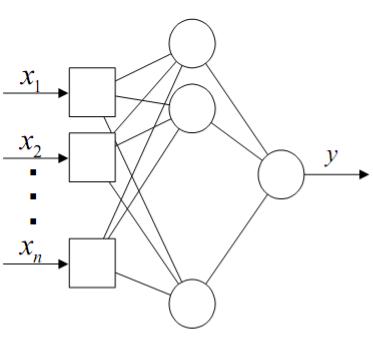
Рисунок 1.14 – Фрагмент нейронной сети
число сигналов (значений) равное
числу нейронов в слое, которые (значения) передаются окончательному выходному нейрону.
Условно это изображено на рис. 1.14 .
Эта последовательность из слоев может быть продолжена и сформирована система из M
слоев. Нейроны каждого слоя получают сигналы с предыдущего и образуют вход для следующего слоя. Так устроены нейронные сети, которые называются сеть прямого распространения
состоящей из M в числе которых M 1 скрытых, и каждый слой содержит Nm , m 1, 2,...M
нейронов. Тогда аналитическим описанием действия нейрона в такой сети служит:
|
f m,i (m,i) |
Nm 1 |
|
|
|
ym,i |
f m,i |
wj m,i ymj |
1,i . |
(1.2.46) |
|
|
|
|
j 1 |
|
|
Соотношение вход – выход слоя запишется так:
ym f m (Wm ym 1 ) ,
где Wm – матрица весов слоя с номером m и ym 1 – вектор значений выхода слоя с номером
m 1. Вся система в целом работает по правилу: |
|
yM lim ym , |
(1.2.47) |
m M |
|
которое обозначим:
130
