
Кобрунов А_Мат методы модел в прикл геоф 2
.pdfГлава 1. Математический конспект
1.1Анализ
1.1.1Базовые математические понятия
Для описания многообразия природных объектов, процессов и связей между ними необходимо использовать некоторые базовые понятия. Поскольку природных объектов,
которыми приходится заниматься в науках о Земле очень много, то для того, чтобы не вводить каждый раз новые сущности, следует позаботиться о том, чтобы введенные базовые понятия были достаточно универсальными и подходить для описания совершенно различных предметов.
Для того чтобы исключить двусмысленности, разночтения и неопределенности эти понятия должны быть строго определены и использоваться только в том смысле, в котором они определены. Единственно подходящими, на эту роль служат математические понятия, которые собственно и возникли для таких нужд – описания некоторых общих свойств окружающего мира с
целью изучения его свойств в конкретных проявлениях.
Первым таким понятием служит переменная.
Переменная – это объект, характеризующийся диапазоном своих возможных значений.
Например – это координата точек, в которых находится измерительный прибор в выбранной системе координат. Координат может включать в себя и время, в которое осуществляется регистрация природного явления. Это пример, когда переменная, в зависимости от ситуации,
может состоять из одного, двух, трех и даже четырех значений. Другой пример переменной это плотность горной породы. Здесь переменная имеет в качестве своего значения одно число. Для образца горной породы можно ввести переменную, характеризующуюся системой из многих чисел. Например, переменная первая компонента, которой есть плотность, вторая – скорость распространения упругих волн, третья – коэффициент температуропроводности. Возможные значения, которые могут принять компоненты переменной, образуют область ее определения.
Это может быть диапазон допустимых значений для одного числа, например как в случае с плотностью, системы чисел, как в случае с координатами или более сложные многокомпонентные
объекты. Наиболее употребительным символом, которым обозначаем переменную, служат x
или y . Обозначения, в зависимости от ситуации могут быть разными. Какой буквой какого алфавита какая переменная обозначается, за редким исключением, которые оговариваются, не имеет никакого значения. Важно лишь то, что определенный символ связывается с переменной и оговаривается, что он обозначает и какова область его допустимых значений. Когда переменная
многокомпонентна – |
например, |
состоит из |
N компонент под символом x понимается |
мультисимвол x {xi |
,i 1, 2,...N} |
или y {yi |
,i 1, 2,...N} Особую роль играет переменная – |
время. |
Оно |
обозначается |
x0 |
или |
t . Множество всех допустимых |
значений |
переменной |
|||||||
x {x ,i 1, 2,...N} |
обозначаем |
D x . Для |
двух переменных |
x1 {x1 |
, x1 |
,...x1 } и |
||||||||
i |
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
N |
x2 {x2 |
, x2 ,...x2 } |
из |
D x |
|
расстояние одной |
от другой обозначим |
d x1, x2 . |
Например, |
||||||
1 |
2 |
N |
|
|
|
|
|
|
|
|
|
|
|
|
d2 x1, x2 |
N |
|
|
2 |
1/ 2 |
|
|
|
|
|
|
|
||
xi1 xi2 |
|
|
. Это обычное Евклидово расстояние. Однако, понятие расстояния |
|||||||||||
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
может |
быть |
определено |
и |
другими |
равноправными |
способами. |
|
Например, |
||||||
d p x1 |
N |
, x2 xi1 |
|
|
i 1 |
x2 p 1/ p
,1 p либо dC x1, x2 max |
|
x1 |
x2 |
|
. |
|
|
||||
i |
|
i |
i |
|
|
|
|
|
|
|
Другое базовое понятие – это функция, синонимом которого служит отображение.
Функция это правило, которое ставит в соответствие одной переменной, например x другую – например y . Функция – это связь между двумя переменными. Собственно изучение этих связей и составляет само содержание – предмет наук об окружающем нас мире, в частности наук о Земле.
Например, функцией устанавливается взаимосвязь между координатами на поверхности Земли и величиной напряженности магнитного поля. Другой пример: функция – это закон, по которому в каждой точке пространства (нижнего полупространства – под поверхностью земли) ставится в соответствие плотность горных пород в этой точке. Функция – это связь которая устанавливает способ расчета скорости распространения упругих волн в зависимости от упругих констант и плотности горных пород. То, что функция, которую обозначаем некоторым символом, например f , ставит в соответствие переменной x , переменную y записывается так: y f x . Та область определения переменной, для которой такая связь определена, называется областью определения функции и обозначается D f . Возможные значения, которые принимает функция f , называется образом D f или множеством значений f и обозначается Im f . Способ, с
помощью которого это правило задано или, синоним – функция определена, может быть различен: табличный, алгоритмический (реализованный на ЭВМ), аналитический в виде математических функций. Это не имеет значение. Важно, лишь то, что для каждого элемента x D f имеется один или несколько элементов y Im f таких, что y f x . Столь общее
определение понятия функции почти не пригодно к практическому употреблению. Следует уточнить такие ее интуитивно понимаемые свойства, как однозначность и взаимо-однозначность,
непрерывность и взаимо-непрерывность. Казалось бы, они подразумеваемы во всех «разумных» приложениях. Однако на самом деле это не так. Если функция f устанавливает связь между скоростью распространения упругих волн v и плотностью горных пород : v f то эта связь вовсе не однозначна – могут существовать образцы пород с различной плотностью, но
42
одинаковой скоростью и для одной и той же плотности могут найтись образцы пород с различной скоростью. Это пример как неоднозначности самой функции, так и ее не однозначности ее обратной. Свойство непрерывности требует для своего определения введения иных – новых понятий, которые, вообще говоря, не связаны с однозначностью. Определить понятие непрерывности для однозначных функций можно следующим образом. Однозначная функция
y f x называется непрерывной, если существует не зависящее от D x и D y , |
конечное |
вещественное число R , такое, что: d f x2 f x1 R d x2 x1 . Разнообразие ситуаций |
|
возникает за счет возможности введения различных мер уклонения переменных на |
D f и |
Im f .
Третье базовое понятие – это оператор. Оператор это закон – закон, по которому одной функции ставится в соответствие другая. Например, это закон, который каждому распределению масс (плотности) как функции координат ставит в соответствие распределение силы тяжести,
создаваемого этими массами. В данном случае этот закон называется законом тяготения.
Оператор может быть и «рукотворным» это например, правило по которому одна функция – наблюдаемые данные преобразуется в другую – результат обработки данных. Оператор обозначаем заглавной буквой алфавита (как и выше не имеет значения какой) и тот факт, что оператор A преобразует функцию g x в функцию u s и записывается в виде
A g x u s . Здесь x и |
s – должным образом определенные переменные для функций g и |
u соответственно. По сути |
своей оператор можно считать отображением одного множества |
функций, называемого областью определения оператора – |
D A в другое, называемого |
областью значений или образом D A при отображении A , |
которое обозначаем, как и ранее |
Im A . Операторы определены законами природы, которые отвечают за преобразование одних закономерностей в другие и определенными алгоритмами преобразования одних наблюдаемых зависимостей в другие. Изучение и конструирование операторов это собственно есть один из важнейших компонентов познания и изучения окружающего мира. Конструирование этих операторов и выявление их свойств путем математического анализа либо компьютерного моделирования это и есть одна из задач математического моделирования. Также как функция в сравнении с переменной имеет более богатый спектр свойств, так как устанавливает законы преобразования одних переменных в другие, а эти законы сами зависят от свойств переменных и взаимной комбинации этих свойств, так и оператор требует введения и изучения гораздо более богатого спектра свойств, чем функция. Следует также, как и для понятия функции установить свойства однозначности и взаимно-однозначности, непрерывности и взаимно-непрерывности операторов. Но уже требование непрерывности для оператора вынуждает как-то определить
43
понятие меры близости двух функций. Дальнейшая схема такова же, как и для определения непрерывности функций. Непрерывным назовем такой оператор, который для каждой ограниченной подобласти в области значений имеет ограниченный прообраз в области определения. Мера близости функций может быть определена многими различными способами.
Причем различными как на области определения оператора, так и на области его значений.
Отсюда и многообразие определений непрерывности оператора и многообразие понятий
непрерывности. |
Например, для двух функций f 1 x |
и f 2 x |
из D A |
уклонение одной от |
|||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
1/ 2 |
|
|
|
другой может быть задано условием: d |
f 2 x f |
1 x |
|
|
|
2 dx |
, а в |
||||||||
|
|
|
f 2 x |
f 1 x |
|||||||||||
|
|
|
|
|
|
D x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
области Im A |
уклонение функции q2 y |
от q1 y |
dC q2 |
y q1 y max |
|
q2 y q1 |
y |
|
. |
||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
y D y |
|
|
|
|
|
|
Тогда непрерывность однозначного оператора может пониматься в том смысле, что существует
некоторая конечная константа R , |
не зависящая ни от элементов из D A , |
ни от |
Im A и |
dC A f 2 x A f 1 x R d 2 |
f 2 x f 1 x . «Степеней свободы» |
в |
понятии |
непрерывности оператора очень много и здесь богатое поле для анализа, результаты которого,
впрочем в большинстве случаев выходят за рамки вопросов моделирования процессов и явлений в науках о Земле.
Следующее базовое понятие – это функционал.
Функционал представляет собой отображение функции в число – скалярное, либо комплексное в зависимости от специфики рассматриваемого вопроса. Для него также используются заглавная буква алфавита, например запись f , означает, что функции f x
ставиться в соответствие число, равное значению f . Например, функционалом служит полная масса некоторого распределения плотности или энергия прошедшего через среду сигнала.
Функционалом является полная энергия сложной системы и по отдельности ее кинетическая и потенциальная энергия. Функционалом служит объем добытого полезного ископаемого в зависимости от функции распределений добычи по координатам и во времени. Функционалом служит величина потерь и риска как функции стратегии поведения. Однако в не меньшей степени понятие функционала необходимо как объект, с помощью которого анализируются и конструируются необходимые для вычислений объекты. Область определения функционала
обозначается D , а область значений – скалярные либо комплексные числа. Для того чтобы определить понятие непрерывности функционала, также как и в случае с оператором надо определить понятие уклонения одной функции от другой на области его определения. Если такое понятие определено, то функционал непрерывен, если модуль разности его значений для любых
44
двух функций из области определения мажорируется мерой уклонения этих функций друг от друга.
Следующий класс базовых объектов связан с понятием случайности и основан на понятии о случайной величине.
Случайная величина это переменная, каждому значению которой в соответствие поставлена вероятностная мера P x , определенная следующим образом. Для любой окрестности x точки x определена функция 0 P x 1 такая, что:
для пустого множества , P 0 ;
P D x 1;
для любой системы непересекающихся множеств xi : P xi P xi .
|
|
|
|
|
|
|
i |
Тогда |
P x |
lim |
P x . |
|
|
|
|
|
|
|
x x |
|
|
|
|
Мера P x это ни что иное, как хорошо известная плотность распределения вероятности, |
|||||||
с которой связан интегральный закон |
x |
P d ; |
распределение вероятностей для |
||||
|
|
|
x |
|
|
|
|
величины |
x , от которого операцией |
дифференцирования |
|
x |
P x легко перейти к |
||
|
|
||||||
|
|
|
|
|
|
x |
|
распределению плотности вероятностей. Введенное определение не строго так как следовало бы уточнить то, что объединение и пересечение счетного числа окрестностей снова принадлежат
D x и, кроме того понятие меры может быть определено на совершенно ином множестве элементам которого поставлены в соответствие значения переменных x . Осреднение случайной величины y f x это операция:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
M f x |
|
|
|
f |
x d x |
|
f x P x dx . |
|||||
|
|
|
|
|
|
|
D x |
|
D x |
|||||
Например, в случае |
f x x |
|
это |
обычная операция вычисления математического |
||||||||||
ожидания. В случае, когда f x |
|
|
|
|
|
|
2 |
|
|
|
|
|||
|
x |
|
|
|||||||||||
|
x |
|
, величина M f |
x есть дисперсия. Таким образом, |
||||||||||
случайная величина это пара [D x , P x ].
45
Если |
для каждого x D x |
определить случайную |
величину y x с областью |
определения |
D y и вероятностной |
мерой y , то это |
отображение следует назвать |
случайной функцией. Обозначать ее будем. [ y x , y x ] . Таким образом, случайная функция
– это параметрически зависящая от x случайная величина с распределением вероятности также зависящим от x .
Флюктуирующие (хаотичные) величины.
Классом случайных величин не исчерпываются все величины отличные от детерминированных. Существуют величины, значение которых также не определено, либо определено некоторым допустимым интервалом значений, для которых отсутствует понятие вероятности. Точнее говоря, выполняя измерения этой величины и повторяя измерения многократно, получаем различные результаты, гистограмма которых при стремлении числа измерений к бесконечности не сходится ни к какой функции – не имеет предела. Строго говоря, в
этом нет ничего удивительно, так как существование предела или вероятности для каждого из возможных значений для дискретной величины или интервала для непрерывной величины, это особое свойство, которое не обязано появляться автоматически. В качестве экспериментального генератора подобного рода величины можно воспользоваться следующим приемом. Из генератора нормальных случайных величин со стартовыми параметрами среднее 0 и
стандартом 1 делается выборка одного значения – x0 , которое принимается за новое
среднее 1 . Из так распределенной величины делается новая выборка величины x1 , которая
далее опять принимается за новое среднее 2 , и делается новая выборка величины x3 . Так
получается ряд значений xi , гистограмма для которой не сходится на к какой функции. Ее поведение при наращивании мощности выборки принципиально меняет свой характер. Величина плотности вероятности для каждого значения (или интервала) сама оказывается случайной величиной. Для такого рода объектов не приемлемы понятия теории вероятностей, поскольку отсутствует само понятие вероятности. И вообще говоря, мир такого сорта объектов больше чем мир детерминированных и случайных величин. Эти величины и объекты не подчиненные никаким вероятностным законам можно назвать хаотичными, а их значения флюктуирующими.
В современной математике единого общепринятого определения для понятия хаоса и определения меры хаотичности нет. Вместо этого вводится понятие динамической системы,
которая генерирует поведение (решения, зависящие от начальных данных) принимаемое за хаотическое. Вводятся понятия корреляционных интегралов служащих индикаторами хаотичных систем. Основным объектом изучения в теории хаоса служат нелинейные динамические системы в пространстве больше, чем двух измерений (по теореме Пуанкаре Бендиксона в линейных либо менее чем трехмерных системах хаотическое поведение не проявляется), и те предельные
46

траектории, называемые аттракторами, к которым сходится их поведение. Это определение и предмет исследований лежат несколько в стороне от наших утилитарных целей, поэтому далее понятие хаотической величины вводится аксиоматически как результат действия машины хаоса.
Хаотическое состояние рассматривается как первичное базовое понятие.
Хаотичность принципиально отлична от случайности. Но обращение с ней возможно по некоторому подобию того как это делается со случайными величинами.
Введем некоторые понятия. Хаотичная величина характеризуется мерой хаотичности
и амплитудой хаотичности . Это числовые характеристики хаотичной величины. Саму хаотичную величину можно представить как итог действия машины хаотичности (хаос-машины) 
с мощностью на параметр , причем разброс значений параметра относительно исходного значения за счет действия машины хаотичности не превышает величины . Эта машина
хаотичности может действовать как на детерминированную так случайную или хаотичную
величину. Пример такой машины был приведен выше на основе генераторов случайных величин.
Другой пример хаос-машины доставляет процедура топологического смешивания, состоящая в последовательном многошаговом перемешивании поля величин. Эта процедура может рассматриваться как аналог введенного выше генератора на основе выборок случайной величины. Хаос-машину можно назвать генератором  хаотизации параметра
хаотизации параметра
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
: |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проявление эффектов хаотичности в наблюдаемых величинах может и меть своим |
|||||||||||||
источником: |
|
|
|
|
|
|
|
|
|
|
|
||||
|
1. |
Хаотизация |
|
наблюдаемого параметра с помощью машины |
, |
|
: |
, |
|
x |
|
||||
|
|
|
|
|
|
||||||||||
|
|
(мультипликативная хаотизация); |
|
|
|
|
|
|
|
||||||
|
2. |
наложение на наблюдаемую величину х составляющей имеющей хаотичную природу |
|||||||||||||
|
|
x |
|
, |
|
x |
(аддитивная хаотизация). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Эти понятия позволяют оперировать с моделями входных сигналов в предположении, что они осложнены искажениями, имеющими мультипликативную и аддитивную хаотическую форму,
которая наложена или осложнена традиционными статистическими помехами. Конструирование средств выявления регулярных компонент полей на фоне хаотических осложнений представляет актуальную задачу обработки геофизических данных.
1.1.2 Гильбертовы пространства функций
Множество функций можно рассматривать как объект аналогичный множеству векторов или множеству чисел. Для этого рассматриваемые функции должны быть объектами одного класса – зависеть от одних и тех же переменных. Их можно было бы складывать и получать новую
47

функцию того же класса, умножать на числа. Так организованные множества функций называются линейными функциональными пространствами. Например, множество непрерывных в заданной области функций это линейное функциональное пространство. Действительно, поскольку линейная комбинация непрерывных функций это снова непрерывная функция то их множество образует линейное пространство. Но множество положительных непрерывных функций линейного пространства не образует, поскольку умножение на отрицательное число выводит функцию и з класса положительных. Общее определение таково.
Линейное функциональное пространство X это множество элементов x X ,
являющихся функциями от некоторых общих для всех функций переменных таких, что вместе с любыми двумя элементами оно содержит и любую их линейную комбинацию. Если эта линейная комбинация образована из вещественных чисел, а сами элементы x X это вещественные же
функции вещественного переменного, то X вещественное пространство.
Линейное пространство Гильберта это функциональное пространство H , которое состоит
из функций f H : |
|
|
|
|
|
|
|
|
|
|
1. |
Образующих линейную систему над множеством (полем) скалярных |
либо |
||||||||
|
комплексных |
чисел1; |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
2. |
Имеющих для любых двух элементов f и g скалярное произведение, f |
g * |
которое |
|||||||
|
определяет норму |
функции f по правилу |
|
H |
f |
|
f * 1/ 2 и служащей |
метрикой |
||
|
f |
|
||||||||
|
d f функции |
|
|
|
|
|
|
|
|
|
|
f . |
g * комплексно сопряженная с g функция. Если рассматриваются |
||||||||
вещественные пространства (в основном рассматриваются именно вещественные функции вещественного аргумента) то знак сопряжения «*» опускается. Также опускаем
индекс H при символе |
|
там, где ясно, о какой норме идет речь, или это не имеет |
значения. |
|
|
Теперь поясним сказанное.
1. Линейная система это множество H , состоящее из конечного либо бесконечного числа
элементов, таких что: их можно умножать на действительные либо комплексные числа в итоге результат снова принадлежит H ; сумма любого конечного числа элементов из H должна снова принадлежать H . Это последнее утверждение можно записать так: для любых чисел i и
элементов fi H ( i , fi H ) i |
|
; i fi H . |
||
|
|
|
|
i |
2. Скалярное произведение f |
|
g* |
обладает свойством: |
|
|
||||
1 По умолчанию будем в общих рассмотрениях подразумевать поле комплексных чисел.
48

|
|
i fi |
g* |
i fi |
|
g* ; |
|
|
|||||||
|
|
i |
|
i |
|
|
|
f |
|
f * 0 и равенство нулю достигается только при |
f 0 . |
||||
|
|||||||
Далее скалярное произведение двух функций f и g записываем без символа звёздочки,
подразумевая его, если рассматриваются пространства функций с комплексными значениями.
Из свойств скалярного произведения вытекают свойство нормы:
а. 
 f
f 
 0 ;
0 ;
б. |
|
|
|
f |
|
=0 только при |
f 0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
в. |
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
г. Неравенство треугольника: |
|
|
|
f g |
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
g |
|
; |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
Неравенство Коши-Буняковского: |
|
|
f |
|
g |
|
|
|
f |
|
|
|
g |
|
, |
причем равенство |
имеет место |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
только в |
случае линейной |
зависимости |
|
f |
и |
g : а g . |
Для элементов fi |
их линейная |
|||||||||||||||||||||||||||||||||||||||||||||||
комбинация это i fi где i вещественные либо комплексные числа в зависимости от того
i
какой тип функций, комплексные либо вещественные рассматриваются. |
|
Линейная комбинация любой подсистемы |
(части системы f ) линейно-независимых |
элементов образует линейное подпространство H |
пространства H . Линейно-независимые это |
такие элементы fi ,i 1, 2,... ., что из равенства i |
fi 0 следует, что все числа (комплексные |
i
либо вещественные) i равны нулю. Размерностью пространства (подпространства) называется наибольшее число линейно независимых элементов в нем.
Если число линейно независимых элементов, конечно, то и подпространство H
называется конечномерным. Зафиксированную систему линейно независимых элементов fi в
гильбертовом пространстве H можно рассматривать как базис таким образом, что любой другой элемент g этого пространства (подпространства) выражается в виде линейной комбинации элементов fi . В этом случае говорят, что пространство H натянуто на элементы fi . Одно и то
же пространство может быть порождено различными системами линейно-независимых элементов – различными базисами. Переход от одного из них к другому аналогичен преобразованию системы координат в Евклидовом пространстве. Если в линейном подпространстве выбран базис, то от него можно перейти к другому gi той же размерности с помощью системы линейных преобразований. Эти линейные преобразования задаются
49
квадратной матрицей с элементами ij |
так, что g j ij fi |
ij fi . Очевидное условие |
|
i |
|
состоит в том, что эта матрица должна быть не вырождена. В противном случае получаемая
система элементов gi |
будет не полна в H . Это значить, что ее линейная оболочка – все элементы |
||
вида qk jk g j |
с любой матрицей { jk } образуют линейное подпространство H H в |
||
j |
|
|
|
H (собственное подпространство – условие строгого включения H H ). |
|||
Ортогональными называются функции f и g , такие, что f |
|
g 0 . Это обозначается |
|
|
|||
так: f g .
Ортогонализация. Понятие ортогональности позволяет ввести понятие взаимно ортогональных подпространств Hi ,i 0,1,... в Гильбертовом пространстве. Два
подпространства называются взаимно ортогональными, если все элементы одного из них
ортогональны всем элементам другого. Это можно записать так: Hi и H j |
взаимно ортогональны, |
||||
если для любого f H1 |
и g H2 элементы f |
и g ортогональны – |
f |
|
g 0 . Или H1 H2 |
|
|||||
Разложение Гильбертова |
пространства H на |
взаимно ортогональные |
|
подпространства Hi |
|
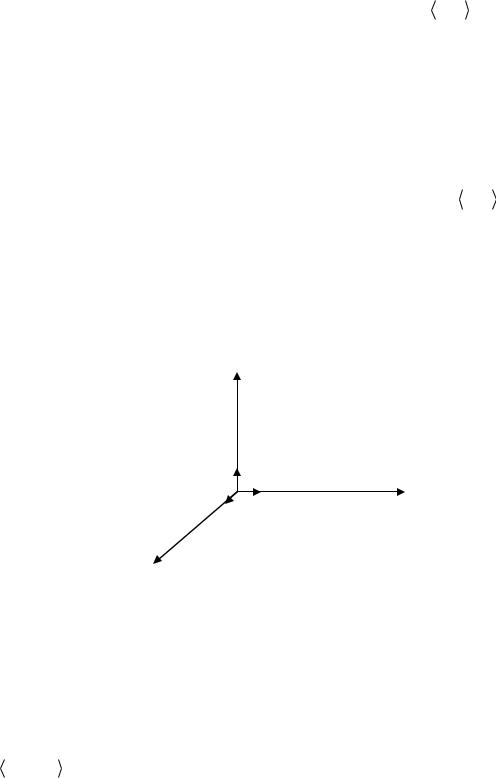
подобно представлению трехмерного пространства R3 в виде трех взаимно ортогональных плоскостей.
|
f3 3 e3 |
H3 |
H2 |
|
e1
e3
|
e2 |
|
f1 1 e1 |
|
|
|
H1 |
|
|
|
|
|
f2 2 e2 |
|
|
|
|
|
|
Рисунок 1.1 – Ортогональные элементы
Если H линейное подпространство в H и элемент g принадлежит дополнению H до
H , которое обозначается H H / H (принадлежит H но не H ) то ортогональная проекция
g на H |
это такой элемент g из H , что g g ортогонально любому |
элементу из H : |
||
g g |
|
h |
0 для любого h H . На этой основе можно добиться того, чтобы |
базис гильбертова |
|
||||
|
|
|
|
|
50
