Кобрунов А_Мат методы модел в прикл геоф 2

На практике при выполнении физического моделирования приходится иметь дело лишь с частично подобными объектами, поскольку абсолютное подобие – динамическое, оказывается технически недостижимым.

Изучение динамического подобия требуется при математическом моделировании процессов с использованием физических свойств горных пород, измеренных на образцах кернового материала. Имеет место практика, когда физические свойства горных пород,

измеренные на образцах кернового материала, используются для математического моделирования процессов и явлений объекта в целом – в более крупном масштабе. Например,

при изучении движения массивов горных пород, складкообразования, формирования соляно купольной тектоники. На этом пути возникают системные ошибки, имеющие природу не учета некоторых компонент подобия и отсутствия подобия параметров окружающей среды параметрам естественного залегания горных пород в массиве при измерении свойств. Это ведет к нарушению динамического подобия и ошибкам в результатах моделирования. Расчетная модель движения не соответствует реальным движениям с теми же параметрами. Расчетные скорости распространения упругих волн не соответствуют реальным скоростям. Образец горной породы в массиве это совсем нечто иное, чем выведенный на дневную поверхность с другими термобарическими условиями. Так, например, при изучении упругих свойств горных пород далеко не тривиальна проблема динамической подобности образца и массива горной породы, из которого этот образец извлечен. Она, во-первых, требует тщательного подбора диапазона частот для датчиков и излучателей в процессе изучения и их масштабного согласования с теми волнами,

с помощью которых планируется изучение свойств реального объекта. Во-вторых, требует учета зависимость изучаемых свойств от масштаба изучаемого объекта. Выбирая высокие частоты для изучения образца мы, на самом деле изучаем свойства, отнесенные к этому узкому диапазону частот, которые отличны от свойств на других частотах излучения. В какой мере значимо это отличие чаще всего можно только предполагать.

Неизменным правилом служит: размерности измеряемых – базовых величин и размерности тех явлений и процессов, которые моделируются, должны соответствовать друг другу. Факт этого соответствия служит хорошим контролем «правильности» формул моделирования. Более того, соображения о размерностях величин могут зачастую подсказать уравнения связи между различными моделируемыми величинами при выявлении уравнений

241

состояния, дополняющих законы сохранения при построении уравнений моделирующих явление или процесс.

2.2.3 Формула размерностей и П – теорема

Результатом моделирования служит величина f , связанная с измеряемыми величинами соотношениями f , , ... . Все участвующие в моделировании величины

распадаются на первичные, образующие собственно базовую систему единиц и вторичные,

которые (а точнее значения которых) получаются с помощью расчетов по результатам измерения первичных величин. Например, скорость – вторичная величина, получается расчетом по результатам измерения времени и пройденного за это время расстояния. А вот путь и время – первичные величины. Вообще говоря, какие величины принимать за первичные, а какие за вторичные – не является некоторой продиктованной природой необходимостью. Можно,

например скорость и время принять за первичные величины, а расстояние определить как вторичную по результатам измерения скорости и времени движения. На самом деле роль первичных величин, как правило, играет базовая система единиц (например, СИ).

Пусть два различных объекта имеющие номер 1 и 2 характеризуются значениями величины f : f 1 , 1 , 1... и f 2 , 2 , 2 ... . Если от единиц измерения , , ... перейти к

другим масштабам (например, сантиметры заменить на метры, а граммы – на тонны), то вновь полученные величины будут f x 1 , y 1 , z 1... и f x 2 , y 2 , z 2 ... соответственно. Здесь

x, y, z – масштабные множители. Но для того чтобы законы при этом не изменились отношение величин первого ко второму как для старых так и для новых масштабов должно сохраниться. Это

дает

Дифференцируя последнее выражение по x , и приравнивая x, y, z единице, получим:

242

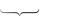
откуда легко сделать вывод:

с некоторыми степенями первичных умноженных на любую константу. Это очень важный результат, поскольку задает вид уравнения, в форме которого следует искать модель изучаемой и моделируемой вторичной величины.

Критерии подобия. П – теорема.

так, что эта связь при изменении масштабов (размерности) не изменяется. Иными словами

уравнение (2.2.2) есть инвариант при изменении масштабов. При этом k из этих размерных

величин 1 , 2 ,...., k первичные, и что очень важно независимые по размерности. Остальные

В последнем выражении k единиц введено лишь для того, чтобы показать высвобождающиеся места в зависимости n 1 величины, переходящую в связь между n k 1

безразмерных критерия подобия. Кроме того, как следует из (2.2.1):

243

Действительно, обращение в ноль определителя означает, например, линейную зависимость между строками. Но именно это и означает линейную зависимость в размерностях.

2.2.4 Примеры применения

Пример 1. Приводимый ниже пример взят из работы [13]

244

Рассмотрим вопрос о фильтрации жидкости в пористых средах. Принимаем следующие

параметры характеризуют свойства проницаемости среды. Этот закон принимаем за уравнение связи. Размерности определяющих параметров (параметров от которых по нашим предположениям зависит моделируемый коэффициент пропорциональности c ):

объему за единицу времени. Таким образом общее число параметров n 4. Из них первичных k 3. Тогда критериев подобия n k 1.

Независимые по размерности это параметры v, d, . k p безразмерный, четвертый параметр. Размерность параметра c получается из остальных по правилу:

c v 0 d 2 .

Кроме того может быть введена любая скалярная функция kp от скаляра, так что

Это уже записанный ранее в разделе 2.1.4. закон Дарси. Методом теории размерности мы обосновали вхождение в него параметров вязкости и проницаемости. Для этого потребовалось лишь перечислить параметры, от которых этот коэффициент может зависеть.

245

Пример 2. Рассмотрим процесс проходки скважины (пример взят из [14]). Будем считать,

что скорость проходки v вдоль ствола скважины зависит от:

G – осевая нагрузка на долото;

– скорость вращения долота;

Q – объемный расход промывочной жидкости;

D – диаметр долота;

Pш – твердость горных пород;

E – модуль упругости материала трубы;

S – площадь поперечного сечения колонны;

L – глубина ствола скважины.

В этом случае таблица размерностей для введенных физических величин – таблица 2.3.

Выберем в качестве независимых переменных величины , D, Pш . Проверка на независимость из условия (2.2.5) дает:

Таблица 2.3

246

Требуя равенства показателей числителя и знаменателя при одноименных базовых переменных получим:

Таким же образом находим и для других Пi критериев подобия:

247

Таким образом, искомую зависимость скорости проходки следует искать в виде:

Введенные переменные, таким образом, связаны в 4 комплекса. Конкретный выбор вида функции должен осуществляться на основе анализа экспериментального материала путем подбора четырех скалярных параметров. Например, это:

Это уравнение следует воспринимать как подсказку в конструировании конкретной зависимости (2.2.7). Оказывается ее надо искать в форме (2.2.8) а не произвольного вхождения семи аргументов. Например, в виде мультипликативной комбинации этих комплексов – критериев подобия. Далее начинается уже другой этап экспериментальных исследований,

направленных на конкретизацию коэффициентов, участвующих в зависимости (2.2.9) или другой принимаемой априори.

248

Глава 3. Системный подход в построении моделей

Необходимость системного подхода в построении моделей геологических сред определена несколькими фундаментальными обстоятельствами, связанными со сложностью и многокомпонентностью изучаемых объектов. Прежде всего, целое – геологический объект это не есть просто суперпозиция своих элементов, но объединение их внутренними взаимосвязями и взаимовлияниями, превращающих эти элементы в целое, наделенное новыми качествами. И в этом новом качестве изменение одного компонента влечет перестройку и переорганизацию всей системы. Например, изменение плотности как одного из элементов системы параметров,

характеризующих геологический объект, тут же влечет за собой необходимость изменения скорости распространения упругих волн, пористости, проницаемости, других геомеханических характеристик, превращая тем самым исходный геологический объект в совершенно иное образование. Изменение плотности ведет к изменению гравитационного поля, но через связи внутри объекта и к изменению других наблюдаемых эффектов – поля времен в сейсморазведке,

электрических параметров, измеряемых в скважинах. Варьировать один параметр при реконструкции модели среды вне взаимосвязи с другими неправомерно. Далее – многокомпонентность объекта изучения ведет к многокомпонентности его проявления в наблюдаемых физико-геологических эффектах. Рассматривать их следует совместно с взаимозависимостями между ними, предопределенными зависимостями между элементами,

складывающими объект. Наконец сложность моделей сред влечет за собой проблемы эквивалентности в решении соответствующих обратных задач в связи с чем последние следует рассматривать только с доопределяющими условиями, следующими из факта существования взаимосвязей и взаимоопределенности элементов. Системный анализ включает в себя два крупных этапа. Во-первых, это собственно системный анализ модели, итогом которого служит формирование непротиворечивой и достаточно полной математической модели компонент изучаемого объекта с определением их иерархической организации, взаимосвязи и параметров,

входящих в описание модели. Это системный анализ данных. Другим крупным этапом служит формулировка задачи реконструкции параметров объектов (среды или процесса) на основе построенной системной модели. Это – задача реконструкции физико-геологической модели среды или процессов, обусловивших наблюдаемые данные, называется задачей системной инверсии, в отличие от методов моноинверсии как формальных постановок обратных задач для конкретно выписанных операторов для одного метода. Задачи системной инверсии формируются на языке уравнений, ограничений, функционалов качества. К уравнениям относятся, в том числе, и

нечеткие отношения, к ограничениям и функционалам качества большой набор средств выражения взаимосвязи и принципов, характерных для изучаемой системы.

249

3.1 Модели задач системного анализа и понятия о системном анализе

Особенностью задач математического моделирования в науках о Земле состоит в наличии сложных взаимосвязей между компонентами и параметрами, входящими в описание модели изучаемого объекта, иногда даже полностью не известных и формулируемых на языке нечётких множеств и нечётких отношений. Взаимосвязи между компонентами могут играть решающую роль в задаче изучения особенностей объекта и без этих взаимосвязей должным образом не могут быть поняты.

Рассмотрим уже упоминавшийся выше пример с плотностью горных пород. Хорошо известно, что распространение упругих волн в идеально упругих средах подчиняется волновым уравнениям, в которых определяющим параметром служит скорость распространения продольных волн. Есть теоретическая зависимость выражающая скорость через плотность и параметры упругости. Эта зависимость такова, что скорость обратно пропорциональна квадратному корню из плотности горных пород и прямо пропорциональна корню из суммы

менее, отсутствуют примеры, когда с увеличением плотности скорость уменьшается.

Эксперименты подтверждают, что дело обстоит как раз наоборот. С увеличением плотности увеличивается скорость, в общем-то, по разным законам для разных ситуаций, но всегда увеличивается. Причина состоит в том, что параметр плотности не только определяет скорость, но и сам связан с параметрами упругости весьма сложной зависимостью. Горная порода относительно этих параметров служит композицией с различными связями между параметрами и должна рассматриваться как система. Сложные среды по необходимости это сложные системы,

порождающие богатые системные отношения между входящими в их описание параметрами и процессами. Сложным средам соответствуют сложные многопараметрические данные, анализ которых позволяет делать выводы о строении системы. Это обстоятельство требует относиться к задачам моделирования в науках о Земле как задачам системного анализа, руководствоваться системными принципами при моделировании и анализе данных, которые излагаются далее.

Специализированный аппарат анализа и решения задачи изучения моделей сред и происходящих в них процессов – это аппарат системного анализа. Тем не менее, при всей сложности изучаемых моделей, они отражают лишь упрощённое видение изучаемых объектов в терминах параметров выбранной их модели. Изучаться могут взаимосвязанные между собой модели сред – геологической среды, пластовых систем, горных массивов, зон осадконакопления,

и так далее. Конкретная предметная модель среды есть одна из сторон, проявлений в виде модели соответствующей среды. Изучаться могут взаимосвязанные между собой модели процессов, происходящих в среде – распространение напряжений, деформаций, движение

250