
Кобрунов А_Мат методы модел в прикл геоф 2
.pdf
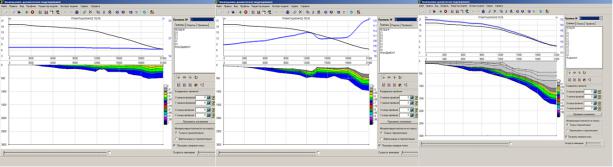
Рисунок 3.4 – Динамика структурной модели и соответствующего гравитационного поля от стартового (слева) с несоответствующим наблюдаемому современному полю до современного
(справа), соответствующего наблюдаемому полю
Эволюционно-динамические уравнения обозначаем:
Dj σΨ , gG ,d ;
σΨ (0) σ0 |
Ψ , gG 0 g0G . |
(3.3.9) |
j 1,...ND . |
|
|
где d – геодинамический параметр, который, в частности может совпадать с одним и компонентов физической модели ФГМ.
Отличие в записи между (3.3.6, 3.3.7) и (3.3.9) состоит лишь в том, что в (3.3.9)
подчёркивается, что компоненты эволюционных законов могут и не иметь форму дифференциальных уравнений, а лишь устанавливать подобие одних компонент ФГМ, с другими,
динамика которых рассматривается. Но в частном случае можно (3.3.9) рассматривать как (3.3.6),
либо даже (3.3.7). Кроме того подчеркнём различие между (3.3.9) и (3.3.1). Она состоит в том, что
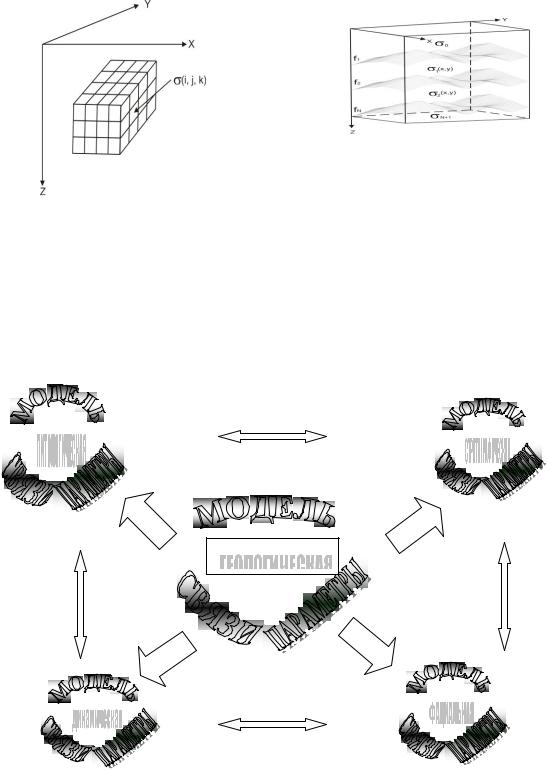
(3.3.1) это алгоритмически определённый закон в соответствии с которым по заданному состоянию одних элементов ФГМ можно сузить, а в исключительных случаях сильно сузить класс допустимых моделей для других компонентов ФГМ, в то время как (3.3.9) есть уравнение развития компонент ФГМ модели во времени, начиная с некоторого начального состояния σ0Ψ , g0G до современного, соответствующего наблюдаемым геофизическим полям. Развитие происходит в соответствии со значениями геодинамических параметров d связанными для всех компонент ФГМ, входящих в систему геодинамических уравнений. Взаимозависимость этих параметров для разных элементов ФГМ и есть то, что объединяет различные компоненты ФГМ в систему взаимоувязанных единым генезисом объектов.
264







 X
X