
Кобрунов А_Мат методы модел в прикл геоф 2
.pdf
4.2.2 Характеристики случайных сигналов
В значительном числе ситуаций сигнал представляется как одна реализация некоторого случайного процесса, которая столь представительна, что исчерпывающе характеризует свойства самого процесса. Такие процессы называются эргодичными и по смыслу ясно, что их свойства не меняются со временем. Иначе бы свойства процесса через некоторый интервал времени изменились, и другая реализация отражала бы эти новые, измененные свойства. Но раз по одной первой реализации можно судить о свойствах всего процесса в целом, то, следовательно, он со временем не меняются. Процесс, породивший этот сигнал, должен быть стационарным – т.е. его свойства неизменны во времени. Не стационарных эргодических процессов, таким образом, не бывает.
Ниже приводится стартовый набор сведений из теории случайных процессов [23]
Практическое значение в задачах моделирования в науках о Земле являются вещественно-
значные случайные процессы. Тем не менее, основные определения приводятся для случая,
включающего в себя случай комплексных значений для процессов. Однако эта общность на самом деле излишняя.
Для двух случайных величин и скалярное произведение определено через
математическое ожидание их произведения |
|
|
* |
|
* |
и |
для |
|
случайного процесса |
|||||
|
|
|||||||||||||
|
|
M |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
определена функция двух переменных t |
|
|
* |
s |
|
|
|
* |
s |
|
, |
которая называется |
||
|
|
|||||||||||||
|
|
|
M t |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
корреляционной функцией. Здесь символ * обозначает сопряжение. Оно состоит из перехода к комплексно сопряженным числам (обозначается чертой сверху) и замены последовательности значений организованных в столбец на ту же последовательность, но организованную в строку:
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
; * |
|
2 |
|||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
Ковариационная функция это |
|
* |
s |
|
|
|
* |
s . |
|
cov t , s M t |
|
|
M t M |
||||||
|
|
|
|
|
|
|
|
|
|
В дальнейшем используется следующее уточняющее предложение. Корреляционной функцией
называется |
|
|
* |
s |
|
. |
Ковариационная |
функция совпадает с |
|||
величина K (t, s) M t |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
корреляционной в случае, если |
M t |
M* s 0 . |
Для |
стационарных случайных |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
процессов, |
характеризующихся тем, |
что величина |
M |
t |
не зависит от времени можно |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
считать, что M t 0 и корреляционная функция совпадает с ковариационной. Кроме, того в
291

этом случае (стационарного случайного процесса) K (t, s) |
зависит лишь от разности аргументов |
||||||
t s , причем: |
|
|
|
|
|
|
|
1. |
Корреляционная |
функция |
четная |
по |
своему |
аргументу |
– |
K(t, s) K(t s) K( ) K( )
2. Принимает только вещественные значения.
Корреляционная функция называется также автокорреляционной, в противовес к
взаимной корреляционной функции. |
|
|
|
|
|
|
|
|
|
|
Для двух случайных |
функций t |
и |
t |
совместная |
корреляционная функция |
|||||
определена как матрица |
|
|
|
|
|
|
|
|
|
|
K t, s |
K t, s |
, где K |
|
|
|
* |
s |
|
. |
|
|
|
|
t, s M t |
|
|
|||||
|
|
|
|
|
|
|
||||
K t, s |
K t, s |
|
|
|
|
|
|
|
|
|
Для стационарных случайных процессов взаимная корреляционная функция K (t, s) также зависит лишь от разности аргументов t s , но не обладает свойством четности. Вместо него
выполнено условие: K |
|
|
* |
s |
|
K |
. |
|
M t |
|
|
||||||
|
|
|
|
|
|
|
|
|
Для трех и большего числа случайных функций она определена как трех и более мерная |
||||||||
матрица. |
|
|
|
|
|
|
|
|
Для случайного |
процесса |
можно |
определить понятие его производной t . Это |
|||||
случайный процесс, к которому |
в определенном смысле сходимости (например, в |
||||||
среднеквадратичном |
смысле) предел lim |
t h t |
. |
Это далеко не |
то же самое, что |
||
|
|||||||
|
|
h 0 |
h |
|
|
||
производная по t |
от реализации |
случайного |
процесса |
рассматриваемой |
как неслучайной |
||
функции. Тем не менее, справедливо утверждение, что корреляционная функция процесса t
равна 2 K t, s и совместная корреляционная функция процесса и его производной определена,
t s
следовательно так:
K t, s |
K t, s |
|
|
K t, s |
K t, s / s |
|||||||||
K |
|
t, s |
K |
|
t, s |
|
K |
|
t, s / t |
2 K |
|
t, s / t s |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Наряду с операцией дифференцирования для случайных процессов может быть велена операция интегрирования:
292
b |
t dt |
lim |
s |
t |
|
t |
, |
s |
– произвольная точка интервала t |
t |
. |
||
|
|
max t |
t |
0 |
i |
|
i 1 |
i |
|
i |
i 1 |
i |
|
a |
|
i 1 |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интегралом является случайная величина, которая существует, например, в том случае, когда процесс непрерывен в смысле средних квадратов. Однако вычислить распределение интегралов от случайных функций достаточно сложно. Но моменты считаются просто:
для случайной функции непрерывной в среднеквадратичном:
M |
b |
t dt |
|
b |
M |
t dt; |
|
|
|
|
|
|
|
|
|
|
a |
|
|
a |
|
|
|
|
b |
|
|
|
b |
|
|
cov |
t dt |
, t |
K t, s dt; |
||||
|
a |
|
|
|
a |
|
|
|
b |
|
d |
|
|
b d |
|
cov |
t dt |
, |
s ds |
K t, s dtds; |
|||
|
a |
|
c |
|
|
a c |
|
b |
d |
|
b d |
cov f t t dt, g s s ds |
f t g* s K t, s dtds. |
||
a |
c |
|
a c |
Следующий результат относится к свойствам линейных преобразований от случайных функций и основывается на приведенных выше соотношениях.
Обозначим A линейный интегральный оператор, действующий на случайную функцию f t по правилу:
b
Af t A t, s f t dt .
a
Интеграл понимается в среднеквадратичном смысле. Функция A t, s непрерывна и абсолютно интегрируема по любому из своих аргументов.
Справедливы следующие равенства:
M A |
t |
AM t ; |
|
|
|
|
|
KA , A t, s AA*K , t, s . |
|||
Если применять оператор A t, s |
к K , t, s |
лишь по первому аргументу, то получается |
|
взаимная корреляционная функция A t и t : KA , t, s AK , t, s . |
|||
Здесь A* – сопряженный к A |
оператор, |
определенный тем, что вместо A t, s |
|
рассматривается ее комплексно-сопряженная, и интегрирование в определении оператора осуществляется по другой переменной – по переменной s :
293
b
A* f A* t, s f s ds
a
Свойство непрерывности в различных его определениях очень важно. Если t ,t [0,1]
независимы друг от друга и имеют одинаковую плотность вероятности, то он не стохастически непрерывен ни в какой точке (стохастически непрерывный процесс определен условием
P |
|
|
|
|
|
|
|
|
|
|
|
t t0 ,t t0 . |
Гарантирующем |
корректность всех |
вводимых |
понятий |
служит |
||||||
среднеквадратичной непрерывности. |
|
|
|
|
|
|
|
||||
Для того, чтобы случайная функция |
t |
была |
непрерывна в среднеквадратичном |
||||||||
необходимо и достаточно непрерывность функции M t |
на множестве |
T или, |
что то же |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|||||
самое непрерывность функции M t |
|
на множестве T T . |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||
Другим видом интегрирования в теории случайных функций является стохастическое |
|||||||||||
интегрирование. |
Его |
простейший частный |
случай |
это |
стохастическое интегрирование от |
||||||
|
|
|
|
|
|
|
|
|
b |
|
|
неслучайных функций. |
В отличие от рассмотренного выше интеграла t dt , от случайной |
||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
функции t , стохастический интеграл |
|
|
|
|
|
|
|
||||
b |
|
|
|
|
|
|
|
f t по случайному процессу t . |
|||
f t d |
t определяется от неслучайной функции |
||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
b |
|
|
|
|
|
Если процесс t дифференцируем, то f t |
d t f |
t t dt и стохастический интеграл |
|||||||||
|
|
|
a |
|
|
a |
|
|
|
|
|
сводится к рассмотренному ранее интегралу от случайной функции – на этот раз произведению
неслучайной функции |
f t |
|
на случайную t . |
|
|
|
|
|
|
|
||
Определение |
этому |
интегралу |
может |
быть |
|
дано |
для |
непрерывных функций f t |
||||
следующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
b f |
t d t |
lim |
f s |
t |
|
t |
. |
||||
|
|
|
max t |
t 0 |
|
i |
|
i 1 |
|
i |
|
|
|
a |
|
|
i 1 |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Предел понимается в смысле средних квадратов и si – произвольная точка интервала
ti 1 ti . Из этого определения следует аналог правила интегрирования по частям:
b |
b |
f t d t f b b f a a t f t dt . |
|
a |
a |
294
В анализе реальных данных, как правило, нет возможности получения множества выборок или иначе – реализаций случайного процесса. В этой связи приходится довольствоваться тем, что есть. Для того чтобы такой возможности придать статус допущения следует ввести предположения о случайном процессе позволяющие судить о его общих свойствах по одной его одной реализации. Таких свойства два. Первое это стационарность процесса. Второе – эргодичность.
Стационарным называется такой процесс, все моменты которого, а это математическое ожидание, дисперсия и более высокие, не изменяются с течением времени.
Эргодичным процессом называется такой, в котором все характеристики процесса могут быть найдены по одной его реализации. Точнее это означает, что интегрирование по ансамблю при вычислении моментов эквивалентно интегрированию по времени в одной реализации случайного процесса.
Эргодичным может быть только стационарный процесс.
Практическим приемом проверки на стационарность служит сравнение результатов вычисления моментов (числовых характеристик) процесса по различным его временным интервалам. В том случае, когда эти результаты совпадают с требуемой точностью или с реализацией выполнены трансформации, обеспечивающие совпадение, процесс принимается за стационарный и эргодичный. Иного пути экспериментальной проверки на стационарность и оправданность предположения об эргодичности при отсутствии возможности повторения эксперимента нет.
4.3 Задачи анализа сигналов
Основной задачей, стоящей перед анализом сигналов служит построение их моделей Нужно это для того, чтобы подготовить измеренные данные к виду для последующей реконструкции свойств модели среды и модели информационного канала. Для этого следует его найти, описать и должным образом представить. В этой связи выделяется три типа задач, стоящих перед анализом исходных данных y x . Это задачи обнаружения, классификации и оценивания
поступившего на вход измерительной системы сигнала.
Обнаружение состоит в ответе на вопрос – есть ли результат измерения y x следствие
появления сигнала x осложненного помехами (шумом) различной природы или это просто
помехи. Эта задача эквивалентна задаче различения полезного сигнала и шума.
Классификация состоит в принятии решения о том к какому виду из заданного перечня сигналов i x ,i 1, N (стандарт – сигналов), принадлежит поданный на вход сигнал x ,
приведший к регистрации y x .
295
Оценивание состоит в нахождении (реконструкции) поступившего на вход измерительной системы сигнала x по результату измерений y x .
Грань между этими задачами размыта. В некотором смысле задача обнаружения может быть рассмотрена как задача классификации – выбора между двумя альтернативными гипотезами – отсутствие и наличие полезного сигнала. Задача оценивания также может быть сведена к задаче классификации из достаточно широкого перечня стандартных сигналов и их комбинаций. Наиболее полной и масштабной задачей служит задача оценивания. По результату оценивания может быть построены алгоритмы классификации, сводящиеся, например, к оценке меры близости результата оценивания и стандарт – сигналов. Также могут быть построены критерии оценки того, есть ли оцененный сигнал шум, либо содержит регулярные компоненты. В
значительном числе случаев все эти задачи могут быть решены при наличии хороших алгоритмов оценивания, основанных на сконструированной модели измерительной системы. Это оценивание состоит в реконструкции на основе сконструированной модели информационного канала входного сигнала по регистрируемому выходному и совокупности предположений входящих в конструкцию модели (предположения о характере преобразований в информационном канале и,
в частности в измерительной системе, характере и взаимосвязях компонент помех,
присутствующих в информационном канале.)
Моделирование информационного канала состоит в формализованном описании процессов трансформации входного сигнала f x при его прохождении по изучаемой системе и
преобразованию во входной сигнал измерительной системы x , дальнейшей трансформации в измерительном канале (измерительной системе). Обратная задача моделирования в теории сигналов это и есть задача оценивания – задача реконструкции входного сигнала. При успешном решении обратной задачи и адекватности реальности построенной модели, удается достаточно точно реконструировать (оценить) входной сигнал и, тем самым достаточно полно представить информацию о входном сигнале, для последующего принятия экономических и технологических решений. Путь моделирования измерительного канала и его фрагментов наиболее распространен и достаточно эффективен. Однако он не является единственно возможным.
Другой путь, получивший развитие лишь в последние годы состоит в выявлении скрытых регулярностей в параметрах сигнала y x и их отождествления с сигналом x . Этот путь основан на проявлении синергетических эффектов при эволюции динамических систем с хаотически распределенными параметрами, и реконструкции регулярных компонент на основе преобразований стохастического резонанса.
Имеется достаточно большое количество учебников и учебных пособий, посвященных проблемами обработки сигналов с целью решения перечисленных задач [24, 25, 26]. Мы направляем к ним для подробного изучения вопроса. Здесь излагаются лишь те вопросы, которые
296
мы считаем необходимым особо подчеркнуть, так как они имеют первостепенное значение при моделировании системы прохождении сигнала и самого сигнала.
4.4 Линейная модель измерительного канала
Конструктивные аналитические результаты при моделировании информационного канала
могут быть получены при введении достаточно жестких ограничений на компоненты задачи.
Первым и наиболее значимым предположением при моделировании информационного канала, служит предположение об отсутствии членов x G f x в изучаемой системе
(рис. 4.1) и, как следствие, возможности включения в измерительный канал мультипликативного преобразования в u x A f x . Это предположение об отсутствии «эмиссии» –
неконтролируемых искажений. Преобразование носит характер операторного действия. Можно считать, что все мультипликативные преобразования осуществляются в измерительном канале, а
преобразующая система отсутствует. Если такое предположение сделать нельзя, то после моделирования измерительного канала следует отдельно позаботиться о моделировании преобразований с целью реконструкции искомой величины – . Эта величина рассматривается как некоторый распределенный параметр. Таким образом, x u x и измеряемая величина y x является результатом мультипликативных и аддитивных искажений u x . Вследствие этого предположения, оценке по результатам измерения y x подлежит u x .
Второе упрощение состоит в том, что перемешивание последовательности мультипликативных и аддитивных искажений входного сигнала u x , а эти операции не коммутируют между собой, заменяется на один раз примененное мультипликативное *N и один раз примененное аддитивное n преобразование. Поскольку эти преобразования, примененные в разной последовательности, дают разный результат (некоммутативные преобразования), то для определенности считаем, что первоначально сигнал искажен мультипликативно, а далее результат подвергся осложнению аддитивной помехой. Это весьма значимое ограничение также как и введенной ранее об отсутствии эффектов «эмиссии». Таким образом, в весьма упрощающих дело предположениях можно принять, что результат измерения y x связан с сигналом u x
правилом:
y x N *u x n .
Под символом «*» понимается операция применения оператора N к u x . Чаще всего
это оператор свертки, с функцией N x , чем и предопределена такая запись. Оператор N
297
может имеет различную природу. Например, это может быть аппаратная функция N0 x ,
искажающая сигнал u x за счет не идеальности измерительного прибора – он на локализованный сигнал отвечает более размытым по переменным x сигналом:
298
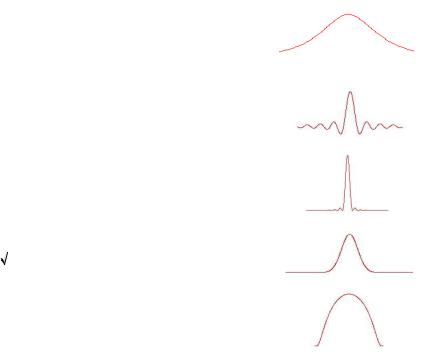
1. N |
|
(t) |
1 |
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
t2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2. N |
|
(t) |
sin(t / ) |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
0 |
( t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3. N |
|
(t) |
|
2 |
sin2 (t / ) |
; |
|
|
|
|
|
|
|
|
|||||||||||||
0 |
|
|
|
|
|
( t)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4. N0 t |
exp( t2 / 4 ) |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
C exp( |
|
|
|
|
|
, |
t |
, |
|
|||||||||||||
5. N0 |
|
|
|
|
2 |
|
|
2 |
|
||||||||||||||||||
(t) |
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
, |
t Rn ; |
||
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 |
|
|
t |
|
/ 1/ 2; |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
N0 (t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
6. |
|
|
|
|
|
|
|
t |
|
/ 1/ 2. |
|
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
||||||||||||||||||
Все они представляют собой отклик на единичный импульс и понятно, что обладают сглаживающим свойством – размазывают энергию локально концентрированного сигнала,
например в нулевом моменте времени на большой промежуток времен. Поэтому восстановить
входной сигнал u t по измеренному выходному y0 t N0 t u d будет достаточно
сложно.
В качестве оператора N может выступать свертка с реализацией некоторой случайной функции, обозначим ее N x о которой известны ее статистические характеристики. Это можно ассоциировать со случайными погрешностями, присутствующими в воспроизводимой аппаратуре.
Наконец, возможна комбинация первого и второго, так, что мультипликативное преобразование сигнала u x складывается из преобразования с известной аппаратной функцией N0 x и
некоторой мультипликативно действующей помехой N x : N x N0 x N x .
Модель измерения в приведенных двух условиях имеет вид
y x y0 x N0 x N x * n x N0 x N x *u x n xN0 x *u x N x *u x n x .
299
Отсутствие мультипликативной помехи N x либо возможность ее сведения к
компоненте N x * u x в аддитивной помехе может быть введено как предположение,
однако оно в целом искажает модель измерения, поскольку эта аддитивная часть зависит от подлежащего оценке сигнала u x .
Аддитивная помеха n x может иметь различную природу и характеризоваться разными способами. Например, это может быть реализация случайного процесса, характеризующегося своими параметрами. Это может быть еще более частный случай – реализации для каждого x
случайной величины, со своей статистикой (плотностью распределения и его характеризующими параметрами – среднее, дисперсия и так далее). Можно считать, например n x состояние параметров динамической системы, в которую «погружен» пришедший извне и подлежащий измерению сигнал. Здесь достаточно много возможностей и частных ситуаций. Но требования конструктивности предполагают выбор с одной стороны достаточно общего вида этой помехи,
охватывающей большинство приложений, а с другой, ведущей к конструктивным результатам.
Таким предположением служит рассмотрение n x как случайной величины (для каждого x ),
характеризующейся своими статистическими свойствами. Чаще всего это случайная величина подчиненная нормальному закону распределения с некоторым математическим ожиданием
M x и дисперсией D x . И, несмотря на то, что существует достаточно много аргументов против такого выбора, он остается, тем не менее, наиболее распространенным, из-за своей конструктивности.
4.5 Реконструкция входных сигналов (принципы)
4.5.1 Задачи инверсии как основа реконструкции
Идеальной была бы ситуация существования такого измерительного прибора или, что почти тоже самое, преобразования R0 над y x , которое приводило бы к «правильным» значениям оцениваемых сигналов u x . Такое преобразование наблюдаемых y x в изучаемый сигнал называется реконструкцией сигналов. В силу существования погрешностей N x и
n x , которые от случая к случаю бывают разные, такого измерительного прибора просто не
существует. Следует выбрать некоторую, в определенном смысле оптимальную процедуру R ,
которая называется процедурой решения обратной задачи или инверсии, которая отображает
(инвертирует) реальные данные y x в возможные значения оцениваемого сигнала. Эта процедура должна быть применима для оценки различных сигналов в рамках одной и той же
300
