Кобрунов А_Мат методы модел в прикл геоф 2

плотностью заряда в точке v в момент времени t . Под термином заряд понимается некий заряд в обобщенном смысле, а не электрический заряд как частный случай. Еще одно замечание.

Произведение плотности заряда, равной Q t, v на вектор скорости его движения v вместе с элементом объема, называется плотность тока J t, v Q t, v v .

Уравнения (2.1.5, 2.1.6) это достаточно общий закон сохранения любой переносимой движущимся веществом величины.

2.1.4 Законы сохранения

Законы сохранения являются центральным звеном всей теоретической физики, которые в самом общем случае постулируют и являются выражениями свойств симметрии уравнений физического поля относительно тех либо иных преобразований. Знаменитой теоремой Э. Нетр установлено соответствие между симметриями и законами сохранения. Конкретно физическое проявление симметрий законов природы реализуются в виде законов сохранения физических величин – массы (заряда), энергии, количества движения. Эти законы не являются, вообще говоря,

независимыми. Преобразование одних форм энергии в другие, взаимопревращение массы и энергии и другие физические эффекты приводят к тому, что более полные, точные и строгие уравнения математической физики, учитывающие подобные явления, не инвариантны относительно некоторых простых групп преобразований (симметрии нарушаются), что и приводит к невыполнению простейших и соответствующих этим группам законов сохранения. Например,

закон сохранения энергии и закон сохранения импульса (количества движения) независимо возникают лишь тогда, когда соответствующее уравнение и его энергетические характеристики инвариантны относительно преобразований сдвига во времени и преобразований сдвига по пространственным координатам независимо друг от друга. Однако по мере достижения большей общности рассмотрений и получении более универсальных уравнений, как правило, происходит все большее удаление от конкретных, требующих решения инженерно-физических задач в рамках классической физики. Установление тех характеристик, которые сохраняют свою величину в индивидуальном объеме, является одной из основных проблем физики.

221

2.1.4.1 Закон сохранения массы

В случае отсутствия внутри рассматриваемой области притока или исчезновения массы формулируется следующим образом: изменение массы в объеме равно потоку плотности ее тока через поверхность, ограничивающую этот объем:

справедливо для любой функции Q t, v весьма полезно и следует из (2.1.4) примененного к

функции t, v Q t, v :

введенное ранее. Последнее равенство, как и его форму (2.1.7) называют также уравнением неразрывности.

222

Приведенное уравнение неразрывности лежит в основе описания многих законов. В

частности оно служит исходным постулатом теории фильтрации. Рассмотрим принципы, лежащие в ее основе.

Пример 1. Первоначальные сведения из теории фильтрации.

Для течения несжимаемой жидкости через недеформируемую пористую среду можно, для скоростей течения v пользоваться уравнением непрерывности div v 0 . Именно это следует из закона сохранения массы. Этим же уравнением можно пользоваться и для стационарного течения сжимаемой жидкости. Условие стационарности означает равную скорость в разных точках и, как следствие равенство нулю производных от скоростей по пространственным координатам.

Основным постулатом в теории фильтрации служит принятие закона о скорости фильтрации в

состояния, которые называются еще и вещественными уравнениями. Функция Φ v зависит от модуля скорости фильтрации и определяет силу сопротивления при движении в пористой среде.

проницаемости, то закон называется линейным законом Дарси а текущая вязкая жидкость –

Ньютоновской жидкостью. Нетрудно видеть, что закон связи скорости фильтрации и градиента

Фундаментальное свойство Ньютоновской жидкости состоит в независимости ее вязкости и как следствия силы сопротивления Φ v от градиента скорости движения. В противном случае жидкость неньютоновская. Подставляя полученное выражение для скорости в закон сохранения получим для ньютоновской жидкости

223

Это эллиптическое уравнение для распределения давлений в пространстве, которое для однородной среды ( , k const. ) трансформируется в уравнение Пуассона:

p v k div f .

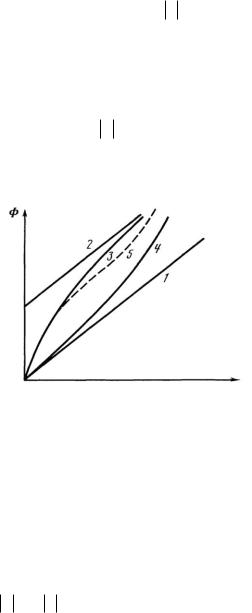
В случае неньютоновских жидкостей, равно как и при не очень медленных движениях ньютоновских жидкостей, возникают отклонения от закона Дарси. Они учитываются нелинейностью функции Φ v (рис. 2.1) и влекут за собой весьма значимые последствия для

процесса фильтрации. Эти последствия визуально можно наблюдать, например, в виде поведения неньютоновской жидкости как упругого тела, если воздействия кратковременны и происходят с большой скоростью. Если встать в ванну, наполненную неньютоновской жидкостью с силой сопротивления Φ v зависящей от прилагаемой силы, то в нее можно погрузиться. Но по ней

можно прыгать и бегать, если Ваши движения достаточно быстры.

1 – Закон Дарси; 2 – закон фильтрации с предельным градиентом давления;

3 – закон фильтрации псевдопластической жидкости; 4 – двучленный закон фильтрации;

5 – закон фильтрации упруговязкой жидкости

инерционных потерь, обусловленных неоднородностью порового пространства. Принятие

Φ v v , 0 ведет к закону фильтрации с предельным градиентом давления. В этом случае движение жидкости в поровом пространстве начинается только после достижения некоторых начальных давлений. Наиболее интересным эффектом наличия пластического сопротивления k G / , где значение G это начальный или предельный градиент давления,

у фильтрующейся вязкой жидкости является образование застойных зон – областей, в которых жидкость не движется, поскольку градиент давления по модулю меньше предельного.

224

Определение формы и размеров застойных зон является основной в прикладном отношении задачей теории фильтрации вязко-пластичных жидкостей, в частности в задачах разработки месторождений вязкопластичных нефтей.

Застойные зоны в частности характеризуют долю нефти, теряемой при ее добычи за счет вытеснения нефти водой.

Все описанные выше возможности могут быть записаны в единообразной форме:

grad p t, v Φ v , k v / v .

Здесь функция f предполагается потенциальной и включена в давление p v . В силу

сопротивления при движении в пористой среде включен и коэффициент проницаемости, что вполне естественно. Чем выше проницаемость, темь меньше сопротивление. Будем считать, что функция сопротивления Φ v , k может быть обращена относительно градиента давления и

Ψ Φ 1 , так что v Ψ v . Тогда с учетом уравнения непрерывности получаем

div Ψ v grad p v ) 0. grad p v

Это эллиптическое уравнение, включающее в себя критические точки, в которых скорость фильтрации равна нулю. Это застойные области фильтрации, в которых нет движения вязко-

пластичной жидкости, в частности высоковязких и парафинистых нефтей.

2.1.4.2 Закон сохранения электрического заряда и уравнения электродинамики

Закон сохранения электрического заряда имеет в точность ту форму, которая содержится в уравнении (2.1.6):

плотность объемного внутреннего притока зарядов за единицу времени в окрестности точки v в

момент времени t .

Пример 2. Уравнения электродинамики.

Закон сохранения заряда, совместно с тождествами из векторного анализа и теории поля,

однозначно приводит к уравнениям Максвелла и многочисленным его приложениям в области моделирования электромагнитных полей.

225

Как известно из теории поля для каждого заряда существует кулоново векторное поле,

дивергенция которого есть рассматриваемый заряд. Оно называется электрической индукцией и

обозначается D16.

div D Q t, v . Также верно и обратное. Каждому кулонову полю соответствует свой заряд, вычисляемый как дивергенция (расходимость) векторного поля. Аналогично, существует векторное поле G, ответственное за плотность внешних источников q t, v . Из соображений удобства возьмем его с отрицательным знаком:

q t, v div G .

Подставляя выражения для заряда и внешнего источника в (2.1.10) получим:

Последнее будет тождеством, если выражение под знаком дивергенции есть ротор некоторого векторного поля H . Назовем его напряженностью магнитного поля. Тогда для H

справедливо первое уравнение Максвелла:

t D J t, v G rot H .

Оно связывает вихри напряженности магнитного поля с изменением электрической индукции, токами J t, v и кулоновым полем G соответствующим плотности q t, v объемного внутреннего притока зарядов. Таким образом, первое уравнение Максвелла это просто переформулированный на языке напряженностей магнитного поля и индукций электрического поля закон сохранения электрического заряда. Но можно ввести и магнитный заряд m , для которого справедлив закон сохранения mt 0 .

Это означает, что магнитные заряды не имеют внешних источников, и их перенос не происходит. Магнитные заряды – это некоторые фиктивные заряды, вводимые для описания магнитной индукции B , дивергенция которой равна величине этих магнитных зарядов. По существу, наблюдая магнитную индукцию, мы можем приписать ей некоторые магнитные заряды по тому же правилу, что и в электростатике – дивергенция индукции равна 4 заряд. Опуская

16Здесь не выписываются постоянные множители типа 4 , которые присутствуют в подобного рода

заменах, поскольку это дело единиц измерения.

226

множитель 4 , как учитываемый выбором размерности величин и используя закон сохранения магнитного заряда, получаем:

B

Но последнее выражение превращается в тождество, если t есть ротор некоторого

векторного поля17 E , который называется напряженностью электрического поля и:18

B rot E .

t

Это второе уравнение Максвелла, являющееся переформулированным на языке магнитной индукции и напряженности электрического поля закон сохранения магнитного заряда.

Если в некоторый начальный момент времени магнитные заряды отсутствовали вовсе и div B = 0,

то это выполняется и во все другие моменты времени в силу закона сохранения магнитного заряда. Следовательно, второе уравнение Максвелла можно дополнить требованием: div B 0 , которое выражает лишь тот факт, что магнитная индукция есть чисто вихревое поле и не содержит дивергентных источников.

Осталось дополнить эти уравнения экспериментальными законами, связывающими между собой напряженность электрического поля и силу тока. Магнитную индукцию и напряженность магнитного поля. Электрическую индукцию и напряженность электрического поля. Эти экспериментальные законы и есть уравнения состояния или вещественные уравнения (уравнения состояния вещества). Они называются также материальными соотношениями или уравнениями материальной среды и формулируются в виде хорошо известных, но, тем не менее,

экспериментальных и потому приближенных, отражающих текущий уровень познания природы,

законов:

пропорциональность электрических полей и индукций: D E ;

пропорциональности магнитных полей и индукций: B Η .

17Для удобства выбираем в равенстве, которое справедливо с точностью до любого множителя, знак минус.

18Это, по существу, закон фарадея, который звучит так: производная по времени потока магнитной

индукции В через поверхность с границей равна циркуляции электрического поля вдоль контура

, взятой с обратный знаком.

227

сил, но действующими внутри объема V . Ее плотность g t, v . Во-вторых, это результирующая всех сил, действующих на поверхность V , ограничивающую объем V . Обозначим эту результирующую f t, v 19 и подсчитаем ее. Для определенности выберем в качестве области V

напряженность соответствующей силы (сила, отнесенная к единице поверхности). Для каждого индекса i объект i j t, v представляет собой вектор τ j t, v (напряжений отнесенной к площадке с номером j ). Для каждого индекса j вектор τi t, v представляет собой три

компоненты напряжен6ий в одном и том же направлении – i , соответствующие трем разным

Последнее выражение – это поток вектора i-напряжений через поверхность,

ограничивающую объем V . Тогда закон сохранения импульса запишется:

Применяя к первому члену правой части формулу Гаусса–Остроградского и переходя от поверхностного к объемному интегралу, в покомпонентной записи получим:

Это и есть закон сохранения импульса. Если воспользоваться уравнением (2.1.4) и законом сохранения массы (2.1.7) при условии несжимаемости среды ( div v 0 ) можно получить, в силу произвольности объема V , следующую его форму:

19 Отнесем ее значение, например к центру области V.

229

Это уравнение называется уравнением движения или уравнением Коши.

В том случае, если среда неподвижна уравнения (2.1.12) трансформируются в уравнения равновесия

div τi t, v g t, v 0 .

Закон сохранения импульса (2.1.12) может быть дополнен уравнениями состояния,

которые отражают априори принимаемые модели сплошной среды. Таких моделей в главном две. Первая – это принятие модели линейно упругого тела. Она состоит в том, что между компонентами тензора напряжений и тензора деформаций существует линейная связь, которая называется законами упругости – законами Гука. Принятие модели упругой среды и закона Гука как ее частного случая ведет к уравнениям распространения малых возмущений – волн в среде.

Это волновые движения и волновые уравнения в их большом поддающемся анализу многообразии. Они будут рассмотрены отдельно. Другая модель – это модель линейно вязкого тела, в котором связь тензора напряжений устанавливается с тензором скоростей деформации (а

не тензором деформации) с использованием параметров вязкости. Эта связь называется законом Навье-Стокса и ее использование в качестве уравнений состояния, доопределяющих закон сохранения импульса ведет к уравнениям Навье-Стокса, описывающих вязкое течение (а не распространение упругих колебаний). Эти уравнения сложно решаются и еще сложнее исследуются. Чаще всего в науках о Земле возможно лишь с их помощью провести моделирование с целью ответа на вопрос – могут ли вязкие течения породить те либо иные структуры, и какие силы этим процессом управляли.

Пример 3. Движение вязкой жидкости. Уравнение Навье-Стокса.

Дополним закон сохранения импульса уравнением состояния связывающего напряжения,

скорость деформации и коэффициенты вязкости.

230