
Кобрунов А_Мат методы модел в прикл геоф 2
.pdf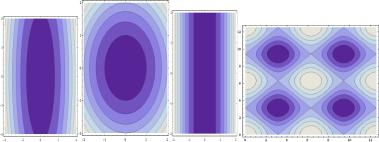
учетом значения вторых производных. Последнее происходит по аналогии с аппроксимацией целевой функции в окрестности выбранной точки параболой и вычислении ее точки минимума.
Здесь шаг задан. Возможны и комбинированные стратегии. Каждая из этих стратегий имеет как свои преимущества, так и свои недостатки. Для строго выпуклых целевых функций, линии уровня которых имеют вид близкий к системе концентрических окружностей (например, в пространстве двух параметров, так как это изображено на втором из серии рис. 1.5) практически одинаково хорошо работают все детерминированные методы.
Рисунок 1.5 – Линии уровня минимизируемого функционала
Разница в эффективности счета и скорости сходимости практически для большинства задач незначительна. Для целевых функций имеющих овражный тип, например такой, как изображено на первом из серии рис. 1.5, объективно должны возникнуть, и возникают проблемы связанные с тем, что значения целевой функции вдоль оси оврага меняются очень медленно. Отсюда малые значения градиентов и изменения градиентов от шага к шагу. Задача оказывается близка к многозначной (не имеющей единственного решения) и продвижение к минимуму идет крайне медленно, сильно завися от того, с какого места это продвижение начато. Привлекательно за счет некоторых случайных переходов выйти из области исчерпавшей себя по скорости сходимости и перейти к другим областям и точкам, чтобы получить представление о распределении иных претендентов на оптимум, возможно и квазиоптимальных элементов. В том случае, если целевая функция имеет много локальных экстремумов или целевая функция выхолаживается так как это приведено четвертом и третьем из серии рис. 1.5, ситуация осложняется еще больше. Попав в окрестность точки локального экстремума, выйти из нее в направлении градиента затруднительно, если только не делать большие шаги в нарушении правил локальной оптимальности. В этих задачах методы, основанные на статистических приемах, становятся наиболее значимы. Но здесь есть одна достаточно не очевидная, но между тем серьезная проблема. Она состоит вот в чем. Если целевая функция имеет сильно овражный вид,
переходящий в вырожденный случай, то детерминированные приемы ведут к оптимальным точкам, зависимым от выбранного начального приближения. Точнее говоря, получаемый элемент, условно (эта идея развивается в разд. 5.3), можно считать ближайшим к нулевому приближению, в сравнении со всеми другими элементами из оси оврага. Это имеет свою
111
положительную сторону, состоящую в том, что свойства получаемого результата, отличающие его от других результатов могут быть точно сформулированы – это ближайший (в соответствующей метрике) элемент из эквивалентных по свойству оптимальности к выбранному нулевому приближению. Стратегии, основанные на статистических методах, возможно, приведут к более быстро получаемому результату, однако что за элемент, полученный в результате, и чем он отличается от множества других, существование которых, очевидно, сказать затруднительно.
Придется в слепую руководствоваться тем, что есть, оставив без ответа вопрос об отличительных свойствах результата в сравнении с другими возможными и способах регулирования вычислительной схемой процессов получения других элементов из множества эквивалентных,
подчиненных заданным условиям.
Учет ограничений на искомые функции или параметры, их характеризующие, должен осуществляться с помощью принципа Лагранжа, в соответствии с которым принадлежность
искомого элемента множеству |
Mi , описываемого в виде неравенств |
Wi |
M i , |
где Wi |
||||
некоторые функционалы, сводится к добавлению в |
целевую |
функцию |
J( f x ) |
членов |
||||
i Wi M |
так, |
что |
минимизируется на |
самом |
деле |
целевая |
функция |
|
i |
|
|
|
|
|
|
|
|
J( f x ) i Wi M |
и числа i должны быть выбраны так, чтобы |
в конечном итоге |
||||||
i |
|
|
|
|
|
|
|
|
выполнялись все условия Wi M i . Приведенная формулировка является далеко не строгой,
но практически единственно конструктивной. Для ее уточнения следует проверить, чтобы экстремали функционалов Wi не совпадали с экстремалью функционала J( f x ) и искомым оптимальным элементом (иначе условия ограничения могут оказаться невыполнимыми). Однако проверить это можно только найдя эти экстремали, а для этого надо решит задачу оптимизации с уже модифицированной по правилу Лагранжа целевой функцией. Далее будем считать, что такое включение ограничений в минимизируемый функционал уже выполнено.
Сведение бесконечномерных задач к конечномерным. Численные методы оптимизации предполагают оперирование с конечномерными множествами и число искомых переменных должно быть конечно. В этой связи бесконечномерная задача
J( f x ) min , |
(1.2.28) |
в которой искомая функция f x есть элемент функционального пространства X |
(например, |
гильбертова) должна быть заменена конечномерной, в которой вместо оптимального f x
ищется конечное число N параметров mi ,i 1 N , с достаточной точностью характеризующее
112
оптимальный элемент f x . Выбрав некоторую, зависящую от параметров mn mi ,i 1 n
систему функций n x,an , которая называется базовой системой функций, |
заменяем задачу |
|||||
(1.2.28) на |
|
|
|
|
|
|
|
J( n x,an ) min . |
|
|
(1.2.29) |
||
Обозначим |
ее решение n x, |
|
n . При соблюдении |
разумных |
правил |
выбора |
m |
||||||
последовательности |
n x,an предел решений задачи (1.2.29) |
сходится к |
решению |
задачи |
||
(1.2.28) при условии, конечно, что все эти решения существуют, что впрочем, относится к числу
«разумных правил формирования задачи (1.2.28) и выбора n x,mn ». Этот прием сведения
бесконечномерной задачи (1.2.28) к конечномерной (1.2.29) называется проекционным методом.
Его название произошло от того, что процедура замены |
f x на элемент n x,mn есть, по |
сути, способ проектирования произвольного элемента из X на многообразие в X образованное |
|
всеми функциями вида n x,mn при всех |
возможных значениях параметрах |
mn mi ,i 1 n . Следует отметить, что вообще говоря, это многообразие нелинейно и может иметь весьма замысловатую структуру. Наиболее распространенным частным приемом проекционного метода служит метод Ритца, состоящий в том, что в качестве базовой выбирается
линейная комбинация |
линейно |
независимых в |
X |
|
системы функций |
n x |
и |
|||
n x,mn mi i x . |
В качестве такой системы, определенной, в частности на конечном |
|||||||||
i 1 n |
|
|
|
|
|
|
|
|
|
|
интервале L вещественной прямой R1 может быть выбрана, например: |
|
|
||||||||
Система алгебраических полиномов n x xn ; |
|
|
|
|
|
|||||
Система тригонометрических полиномов n x ei x 4 |
|
|
|
|||||||
Система функций Хэвисаида: |
|
n |
x 1 |
x n , |
|
n |
– система покрытий |
L так, |
что |
|
|
|
|
0 |
x n |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
n
n i i n, L i . Два элемента из покрытия не пересекаются, а в совокупности
i 1
покрывают все L .
Подобный перечень легко продолжить и распространить на функции многих переменных.
Задачу (1.2.28), которая сведена к конечномерной будем записывать в виде
J m min,
(1.2.30)
m M.
113
Здесь M – ограничения которым должны подчиняться значения параметров. Эти ограничения следуют из физического смысла задачи и наследуют, возможно, краевые и начальные условия на искомую оптимальную функцию. Наличие ограничений вносит специфику в рассматриваемые задачи оптимизации, которая будет рассмотрена отдельно. Можно выделить два класса алгоритмов минимизации. Во-первых, это алгоритмы использующие вычисление производной от целевой функции J m , и алгоритмы не использующие этих производных в явном виде.
1.2.3.1 Минимизация с использованием производных
Градиентные методы используют для своей реализации только первые производные целевой функции J m . Общая формула для продвижения от итерации к итерации в направлении к оптимальному решению имеет вид:
mk 1 mk mk mk k s k mk *k sk . |
|
(1.2.31) |
Из записи (1.2.31) видно, что mk – это вектор перехода от mk |
к mk 1 , s k |
– единичный |
вектор в направлении mk а sk произвольный вектор в том же направлении k и *k скаляры
связанные между собой условием k s k = *k sk .
Простейший градиентный метод, называемый методом наискорейшего спуска состоит в
выборе s k |
|
|
|
J mk |
, где J mk – градиент целевой функции в точке mk . |
||||||||
|
|
|
|
|
|||||||||
|
|
|
J mk |
|
|||||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Градиент целевой функции может быть представлен в виде J mk b Hmk , где b – |
|||||||||||||
постоянный вектор, а H – матрица, не зависящая от mk . Шаг k |
итерационного процесса |
||||||||||||
|
|
|
|
|
|
mk 1 mk k |
|
|
|
J mk |
, |
(1.2.32) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
J mk |
|
|||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
должен подбираться экспериментально. Правило выбора состоит в минимизации целевой функции при переходе от mk к mk 1 . В этом случае движение на каждом следующем шаге осуществляется по направлению ортогональному предыдущему и, следовательно, в идеальном случае выпуклых целевых функций должно завершиться после достижения числа итераций равных размерности множества M .
114

1.2.3.2 Метод Ньютона
Метод Ньютона основан на использовании вторых производных функции цели по параметрам. Его суть определена разложением целевой функции в степенной ряд в окрестности k -ого приближения для нахождения k 1-ого:
J mk 1 J mk T J mk mk 12 mk T 2 J mk mk .
Минимум J m в направлении mk находится приравниванием нулю производных по
компонентам mk , что дает:
|
|
|
mk 2 J mk 1 |
J mk . |
|
|
|
|
|
|
|
Матрица |
2 J mk 1 |
это обратная к матрице вторых производных H mk , которая |
|||
|
|
|
|
|
|
называется матрицей Гессе. Теперь получаем итерационный процесс, соответствующий методу Ньютона;
m |
|
m |
|
|
J m |
|
|
1 |
J m |
|
|
|
|
|
|
||||||
|
k 1 |
|
|
k |
2 |
|
|
k |
|
|
k |
|
(1.2.33) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Если J m квадратичная |
функция, то |
процесс (1.2.33) сходится за один шаг. В |
|||||||||||||||||||
противном случае необходимо вводить длину |
шага |
k и итерационный процесс (1.2.33) |
|||||||||||||||||||
модифицировать к виду: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 J |
mk 1 J mk |
|
||||||||||
mk 1 mk k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 J |
mk 1 J mk |
|
|
|
|
|||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
Эквивалентная запись |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mk 1 |
|
mk |
*k H 1 mk J mk |
(1.2.34) |
|||||||||||||||||
Направление движения определяется вектором sk H 1 mk J mk .
Существует довольно большое число модификаций метода Ньютона и градиентного метода, направленные на улучшение сходимости процесса в различных частных случаях. Обзор этих методов можно найти в энциклопедической работе [1].
115
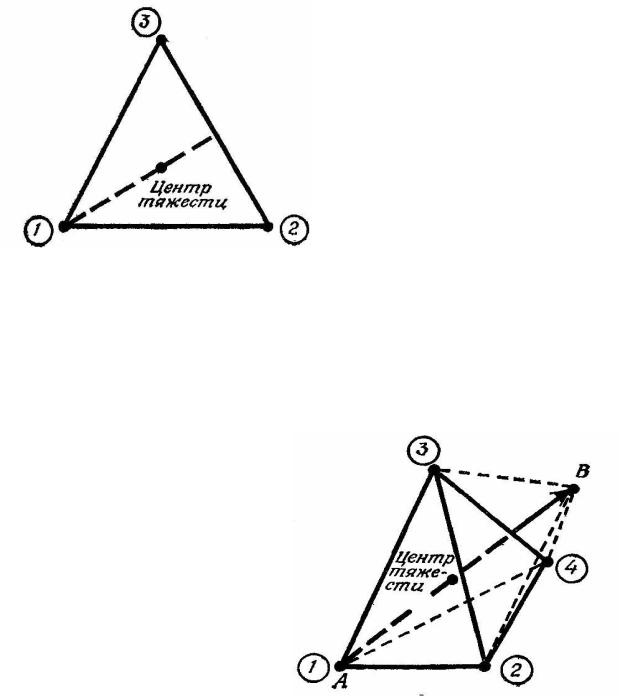
1.2.3.3 Минимизация без использования производных основана на проверке значений целевой функции в некоторой базисной системе точек множества M и нахождении на этой основе очередного приближения к оптимальному элементу. Следующая базисная система точек строится с учетом найденного приближения к оптимальному элементу, и процесс продолжается до достижении требуемой точности. Опишем один из группы алгоритмов,
называемый методом деформируемого многогранника.
|
Если |
множество |
M |
имеет |
||||
|
размерность n , то многогранник в M |
|||||||
|
имеет не менее |
чем |
n 1 вершину. Он |
|||||
|
образует |
|
симплекс. |
|
Например, |
в |
||
|
пространстве двух измерений симплекс – |
|||||||
|
это треугольник с вершинами, имеющими |
|||||||
|
номера 1, 2, 3. |
|
|
|
|
|
||
|
Далее находится вершина, в которой |
|||||||
|
целевая |
функция |
имеет |
максимальное |
||||
|
значение (в данном случае это точка 1) и |
|||||||
Рисунок 1.6 – Симплекс треугольной формы |
через нее проводится вектор в направлении |
|||||||
|
центра |
тяжести. |
По |
направлению |
|
этого |
||
вектора находится новая точка симметричная относительно точки 1, называемая отраженной. Эта новая точка на следующем шаге рассматривается вместо точки 1, которая исключается из последующего рассмотрения. Эти построения для пространства трех независимых переменных приведены на следующем рисунке.
Здесь А – точка с максимальным значением целевой функции J m а В – отраженная (равноудаленная с А относительно центра тяжести). Из оставшихся точек и новой – В строится новый симплекс и процесс продолжается.
Вместо построения точки В по принципу отражения ее положение может быть выбрано как такое, на которой целевая
функция минимальна. Процесс
продолжается до тех пор, пока не будет достигнута либо требуемая точность –
изменение целевой функции меньше порога, либо достигнут заданный предел сходимости – изменение найденных векторов незначительно, либо исчерпано допустимое число итераций. В
116
целом, подобного сорта алгоритмы имеют очень большое число модификаций, отличающихся между собой правилами анализа значений целевой функции в вершинах симплекса и построению на этой основе нового множества узловых точек, в которых сравниваются значения целевой функции. Мера фантазии здесь ничем не ограничена, а многообразие особенностей целевой функции – характера ее линий уровня ведет к возможности конструирования «персональных» алгоритмов, которые подогнаны под особенности решаемой задачи.
Весьма большое распространение получили способы анализа целевой функции J m в
базовой системе узловых значений mi симплекса с последующим формированием правил перехода к новым значениям, получившими название генетические алгоритмы.
1.2.4 Генетические алгоритмы оптимизации
Генетические алгоритмы оптимизации представляют собой специфическую разновидность алгоритмов случайного поиска оптимального элемента без использования производных на основе некоторого стартового набора точек, как и в методах деформированного многогранника. Эти методы хорошо освещены в литературе [1] и широко представлены в информационных ресурсах Рунета. Особое внимание к ним проявляется в связи с достаточно широкими возможностями их применимости – некритичностью к размерности задачи,
возможности использования для сложных целевых функций за счет включения рандомизированных (основанных на случайности) элементах поиска и, что также немаловажно,
современностью используемой терминологии, позаимствованной из генетики. Специфической особенностью методов служит, во-первых, использование кодового представления параметров – например, двоичного кода и, во-вторых применение элементов стохастических процедур для перехода к новой – улучшенной системе параметров. Традиционным для этих алгоритмов является использование терминов: популяция; хромосома; ген; генотип; селекция; скрещивание;
мутации и так далее.
Популяция – конечное множество выбранных параметров, представленных в закодированном виде.
Хромосома – кодовое слово – представление параметр. Чаще всего это двоичный код параметра.
Ген – элементарный элемент кодового слова.
Генотип – набор хромосом для конкретного параметра.
Возможные значения элементов кодового слова – гена – аллель; Чаще всего это значения
1 или 0.
Позиция (номер) конкретного гена в хромосоме – локус.
Классический генетический алгоритм состоит из следующих этапов (рис. 1.7):
117
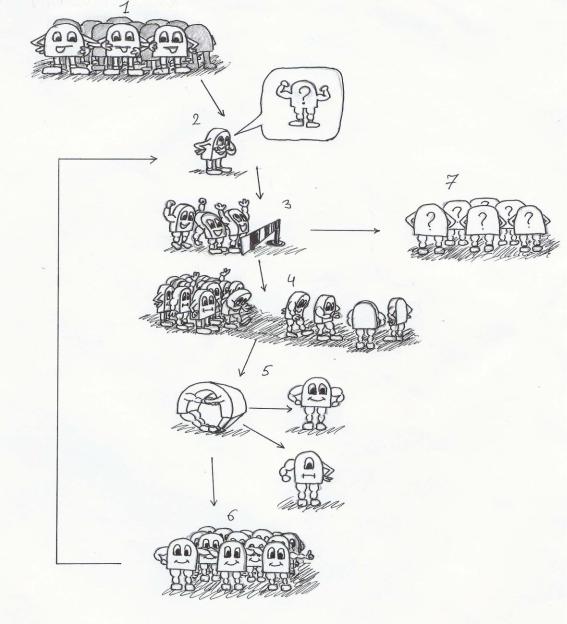
Рисунок 1.7 – Генетический алгоритм. Дружеский шарж
1.Начало – выбор начального набора параметров и их представление в закодированном виде – системе хромосом. Этот этап называется инициализация исходной популяции.
2.Оценка значений целевой функции для популяции.
3.Проверка условия остановки алгоритма. Если оно выполнено – переход на п. 7. В
противном случае
4.Селекция, состоящая в отборе из популяции набора (возможно повторяющихся элементов) для последующего оперирования ими с целью формирования следующей популяции. Этап селекции предполагает присутствие рандомизированной стратегии отбора с учетом значения целевой функции на элементах популяции.
5.Трансформации выбранных в результате селекции элементов, включающую в себя
операции скрещивания и мутации. Они называются генетическими операторами. Это
118
условные названия для процедур получения кодов новой популяции (генотипов). Эти
операции включают в себя элементы рандомизированной стратегии и приводят к
6.Формированию новой популяции. Переход к п. 2.
7.Выбор наилучшего параметра из характеризуемых последней популяцией.
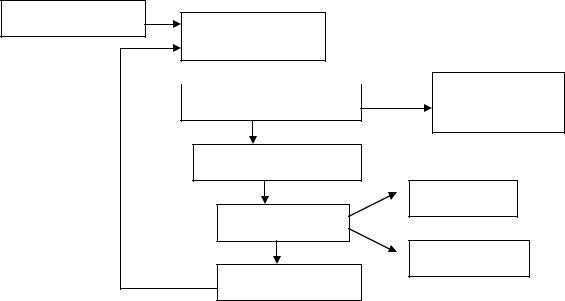
Инициализация
Расчет значений
целевой функции
 Окончательный Оценка оптимальности
Окончательный Оценка оптимальности
результат
Селекция
Скрещивание
Трансформации
Мутации
Новая популяция
Рисунок 1.8 – Граф генетического алгоритма
Чаще всего кодирование осуществляется с помощью двоичного кода. Тогда хромосома представляет собой не что иное, как двоичное представление числа либо системы чисел
заданной длинны. Длинна кода – это длинна L хромосомы, ген это один бит – элемент разрядной сетки, генотип – конкретной число или система чисел в двоичном представлении,
локус – номер разряда. Естественно, что аллель это значение ноль или единица.
В пояснении нуждаются алгоритмы селекции, трансформации и формирования новой популяции.
Селекция это выбор с элементами случайности (рандомизированной стратегии) набора параметров из числа популяции, допущенных к последующей трансформации с целью формирования новой, улучшенной популяции. Селекция осуществляется с учетом выполненной оценки значений целевой функции для популяции. Если текущая популяция представлена
генотипами, соответствующими параметрам mi , i 1 N , и |
J mi оцененные значения |
целевой функции, то мера значимости с точки зрения оптимальности каждого параметра может быть выбрана, например, так:
P mi |
J mk J mi |
|
|
k 1 N |
|
. |
|
|
J mk |
||
|
|
|
|
k 1 N
119

Если теперь сконструировать рулетку (сгенерировать случайные числа) и разбить на N
сегментов, так, что длинна дуги сегмента была равна 2 RP mi где R радиус рулетки, то вероятность попадания шарика в сегмент с номером i будет равна P mi . Сыграв в такую рулетку N раз, получим новый набор параметров mi из числа mi , i 1 N некоторые из
которых могут отсутствовать вовсе а некоторые повторяться тем чаще чем больше величина
P mi . Им соответствующие генотипы называются родительскими. Они допущены для последующего преобразования в новую популяцию процедурами трансформации. Те параметры,
которые не попали в перечень mi отбрасываются. Это естественно, поскольку они не попали потому, что их мера значимости была не высока. Но, конечно еще и дело случая. Таким образом,
итогом процедуры селекции является банк родительских хромосом – генотипов.
Трансформации или генетические операторы. Состоят из двух типов операции – скрещивания и мутации. Скрещивание состоит в выборе родительских пар из числа полученных в результате селекции и перемешивании их генов. Это перемешивание заключается, например в следующем. Выбирается случайным образом число lk из интервала 1 – L 1, где L длина хромосомы и формируются два новых объекта – генотипа из новой популяции. Один состоит на местах от 1 до lk из генов первого родителя, а из lk 1 до L – второго. Другой потомок,
наоборот – от 1 до lk из генов второго родителя, а из lk 1 до L – первого. Мутация состоит в случайном изменении генов у потомков на противоположную аллель (например, нули заменяются единицами, а единицы нулями). Уровень мутации это вероятность, с которой она осуществляется. Если эта вероятность равна нулю, то мутации отсутствуют вовсе.
Новая популяция замещает предшествующую и процесс продолжается.
Как видно элемент случайности «включается» практически на всех этапах. На этапе инициализации это случайный выбор начальных параметров. На этапе селекции это случайный отбор, подчиняющийся заданному вероятностному закону (рулетка с секторами разной площади).
На этапе трансформации случайным является разбиение представителей популяции на пары, и
выбором длинны перемешивания генов в родительских генотипах. Наконец мутации – полностью рандомизированная процедура. Поэтому генетические алгоритмы следует отнести к методам случайного поиска, в котором стратегия этого случайного поиска направляется выбранной моделью эволюции параметров.
120
