Кобрунов А_Мат методы модел в прикл геоф 2

где p – давление.

Если подставить это выражение, выражающее экспериментально наблюдаемый эффект, то получим:

Это уравнение называется уравнением Навье-Стокса. В нем по дважды повторяющемуся индексу происходит суммирование по всем его значениям. Это касается и расшифровки записи

Коэффициенты k и характеризуют вязкое сопротивление при движении среды.

Коэффициент называется коэффициентом сдвиговой вязкости. Он ответственен за скорость изменения формы путем сдвиговых деформаций, а коэффициент k ответственен за вязкость относительно продольных сжатий и растяжений. На самом деле эти коэффициенты не могут быть полностью разделены. Это весьма существенные и искусственные допущения о строении среды.

Если коэффициенты вязкости постоянны, что означает однородность среды, то уравнение Навье-

Стокса существенно упрощается, поскольку эти коэффициенты выносятся из под операции дифференцирования.

2.1.4.4 Закон сохранения энергии или первое начало термодинамики

Закон сохранения энергии или первое начало термодинамики формулируется следующим образом.

Изменение полной энергии системы равно сумме мощности внешних сил, приложенных к системе, и притока энергии за единицу времени.

Запишем этот закон аналитически. 20

20 Суммирование по дважды повторяющемуся индексу предполагается вне зависимости от их взаимного

расположения вверху или внизу

231

потенциальную энергию среды; w t, v – внешний приток энергии – распределенные в объеме положительные или отрицательные источники. Они внешние относительно происходящих процессов переноса; q t, v – вектор переноса (поток) энергии, нормальная компонента которого

равна qn . Будем считать, что внешние источники сил отсутствуют. Это значить, что первое слагаемое в правой части последнего равенства равно нулю. Пользуясь соотношением (2.1.8),

законами сохранения массы (2.1.9) из закона сохранения энергии (2.1.11) а также его формы

(2.1.12), после преобразования поверхностных интегралов в объемные получим:

сохранения энергии перепишется следующим образом:

dt

или уравнение неразрывности;

закон сохранения импульса:

232

t, v v div τi t, v g t, v ;

t

На самом деле это пять скалярных уравнений, поскольку (2.1.12) – это система из трех уравнений по одному для каждой компоненты вектора скорости. В то же время в эти уравнения входит в качестве неизвестных шесть (независимых) компонент тензора напряжений (их на самом деле 10, но в силу симметрии независимых остается только шесть), три компоненты скорости,

плотность, внутренняя энергия, а также компоненты потока энергии. Полученные законы не могут рассматриваться как уравнения для решения, поскольку в них число уравнений существенно меньше числа входящих в них параметров. Для вывода уравнений, конструктивно описывающих те либо иные физические процессы, необходимо полученные законы сохранения дополнить уравнениями связи между различными физическими параметрами, выразив одни параметры чрез другие с использованием специфических свойств среды. Такое выражение основано на физическом эксперименте и носит конкретно-физический характер, например, такой как использованное выше уравнение Дарси. Сами эти связи называются уравнениями состояния. Они конкретизируют физические свойства рассматриваемой среды и уменьшают количество параметров, подлежащих определению. Тем самым законы сохранения трансформируются в уравнения для соответствующего физического поля.

Пример 4. Тепломассоперенос.

Имеется три типичных для математических моделей теплофизики базовых задачи. Это задачи: теплопроводности; конвекции; излучения.

Теплопроводность состоит в переносе тепла без переноса материала – носителя этого тепла. Конвекция это перенос тепла за счет переноса вещества. Наконец излучение это перенос энергии в виде электромагнитных волн. На самом деле реальный процесс переноса тепла в реальных средах включают в себя все эти три компоненты участвующие в разных долях. Вопросы переноса тепла с помощью излучения представляет собой специальный вопрос, который рассматривается как часть теории излучения и поглощения энергии веществом. Она основана на соответствующих моделях переноса излучения.

Для получения уравнения теплопроводности воспользуемся законом сохранения энергии при условии равенства нулю тензора скоростей деформации.

233

где f t, v v w t, v мощность распределенных внутренних источников (теплоты). Далее пользуемся уравнением состояния, которое устанавливает пропорциональность внутренней энергии t, v температуре T t, v с коэффициентом пропорциональности c v равным

удельной теплоемкости среды. Она не меняется во времени. Таковы предположения, хотя они и носят весьма приближенный характер. t, v c v T t, v . Далее делаем предположение,

которое также относится к эмпирическим уравнениям состояния, о том, что тепловой поток

пропорционален градиенту температур, с коэффициентом пропорциональности

Это уравнение называется уравнение Фурье. Оно, по сути, предполагает бесконечной скорость распространения тепла, что конечно есть идеализация. Более реалистичным служит обобщенный закон Фурье, учитывающий время r релаксации теплового потока:

Введенные предположения о независимости от времени (стационарности) физических свойств горных пород, в частности плотности v на самом деле это весьма проблематичны.

Строго говоря, оно и ему подобные не выполняются. Дело в том, что плотность сама зависит от температуры и, как следствие будет зависеть и от времени, в течение которого эта температура изменяется. То же самое относится и к коэффициенту теплопроводности и удельной теплоемкости

среды.

Рассмотрим его частные случаи.

Предположим, что свойства среды не только стационарны, но и сама среда однородна.

Это означает независимость коэффициентов удельной теплоемкости c v и теплопроводности

k v от пространственных координат. Тогда в уравнении (2.1.15) эти коэффициенты могут быть

234

вынесены за знак дифференцирования (операторы градиента и дивергенции) и само уравнение упроститься:

обозначается a v . Обратим внимание на то, что в этом частном случае независимости удельной теплоемкости c v и теплопроводности k v от пространственных координат остающаяся

пространственная изменчивость коэффициента температуропроводности обусловлена изменчивостью плотности, но никак не теплопроводности и теплоемкости. Последние считаются константами.

Другой частный случай состоит в рассмотрении установившегося теплового режима, при

котором t T t, v 0 . Отсюда и из (2.1.15) следует:

Последнее уравнение это уравнение эллиптического типа, которое при его дополнении краевыми условиями и в условиях однородности среды достаточно просто решается.

Следующий частный случай. Среда, в которой происходит распространение тепла, сама может двигаться. Например, течь. Для получения уравнений в этом случае, в соответствии с рассмотрением начала раздела, необходимо частные производные по времени заменить на полные с помощью условия:

dtd T t, v T t, v v grad T t, v .

Теперь из (2.1.15) легко получаем

Член 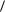v grad T t, v 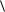ответственен за конвективный перенос тепла.

Если вместо закона Фурье, воспользоваться его обобщенным аналогом, учитывающим время релаксации теплового потока, получим следующее уравнение:

235

Это гиперболическое уравнение второго порядка, в котором вторая производная по времени контролируется параметром релаксации теплового потока r .

236

2.2 Основы теории размерностей

2.2.1 Введение

Для того чтобы изучаемые модели были не противоречивыми и претендовали на адекватное описание изучаемых объектов они должны быть согласованы по размерностям используемых величин. Это универсальное требование. Оно должно выполняться всегда и по этой причине может служить одним из проверочных условий на адекватность модели. Если записано уравнение между физическими параметрами f , , ... , рассматриваемое и пробуемое на модель некоторой связи между параметрами, то размерные величины, , , .. будучи подставленными в это уравнение должны давать размерность величины y . Если это не так, то предполагаемая зависимость не может, служить адекватной моделью. Проверка размерностью – первый и ответственный этап построения моделей. В построенной математической модели размерности всех используемых параметров должны быть соблюдены таким образом, чтобы уравнения не меняли своего вида при изменении параметров. В частности не менялось при использовании различных единиц измерения. В разных системах единиц измерения это должно быть одно и то же уравнение. В этом случае отношение правой и левой части в уравнении модели y f , , ... должно давать скаляр. В некоторых случаях само это условие, и следующие из него выводы помогают в конструировании моделей. Кроме того, весьма распространены задачи реконструкции параметров, характеризующих модель среды по выведенным уравнениям связи и входным данным. Проверочным условием реализуемости такого рода реконструкций служит соответствие размерностей получаемого в результате вычисления параметра, требуемым размерностям, определенным размерностями изучаемого параметра. Отсюда следует также и прием конструирования подобных зависимостей. Одним из его разновидностей, например,

служит переход к реконструкции внеразмерных скаляров, которые называются эффективными параметрами. Одним из многочисленных примеров получения эффективных – внеразмерных параметров служит прием нормирования результатов вычислений размерных параметров к некоторым своим средним оценкам. Таков, например, хорошо известный метод полного нормированного градиента [12] или иные приемы аналогичные приемам яркого пятна. Суть нормирования состоит в следующем. Если предположить, что величина y в уравнении

y f , , ... есть функция некоторой координаты , то переход к безразмерному параметру,

характеризующему аномальные свойства y , может быть:

237

Здесь S – подобласть в области определения , вообще говоря, меняющаяся от точки к

точке . Его очевидным обобщением служит:

При конструировании как физических, так и математических моделей, адекватных изучаемым процессам первой группой вопросов, которые должны быть изучены, служат вопросы о том, какие физические параметры в каких масштабах и единицах измерения должны быть использованы. В какой мере одни те же физические процессы, осуществленные в разных условиях и разных масштабах, могут служить для описания выбранного явления.

2.2.2 Основы теория подобия

Наибольшее значение теория подобия имеет при конструировании физических моделей,

имитирующих поведение некоторого оригинала, не поддающегося прямому изучению. Тем не менее, это важные вопросы и в математическом моделировании, поскольку позволяют рассматривать в качестве аналогов реальных процессов некоторые упрощенные модели с правильно подобранными подобными параметрами. Подобие модели и оригинала основано на подобии параметров, входящих в описание модели параметрам, характеризующим оригинал.

Принцип подобия. состоит в том, что в оригинале и ее модели процессы развиваются подобным образом, если модель и оригинал подобны между собой. Модель и оригинал подобны, если подобны их описывающие параметры. Подобие параметров характеризуется коэффициентом подобия.

Коэффициент подобия это отношение параметра в модели к тому же параметру в оригинале. Если все эти отношения для всех параметров одинаковы, то модель и оригинал подобны.

Модель и оригинал могут быть подобны относительно одних величин, например геометрических и не быть таковыми относительно других, например, времени развития процессов. В этом случае одни и те же значения коэффициентов, характеризующих физические свойства изучаемых объектов, влекут различное развитие процесса. Система оказывается частично подобной оригиналу. Подобие модели и оригинала может вводиться лишь на определенном интервале значений параметра или группы параметров. Например, вязкие среды подобны идеальным жидкостям на одних интервалах времен и хрупким средам на других.

238

Действительно вязкая среда ведет себя как идеальная жидкость на одних масштабах времен – в

миллионы лет и быть хрупким телом, если время приложения нагрузок исчисляется секундами.

Для анализа подобия необходимо рассчитывать отношение величины системного

(измеряемого в заданной системе единиц) параметра в модели к величине аналогичного параметра в оригинале. Напомним некоторые основные, используемые единицы. Система единиц СИ, на основе которой строятся все остальные величины, сведена в таблицу 2.1.

Таблица 2.1

*- дополнительные единицы.

Для длин площадей и объемов коэффициент подобия задается простым соотношением:

площадь и объем, используемые в модели для описания lo , So ,Vo – длинны площади и объема

модели к характерным временам и массам в оригинале.

239

Геометрически подобными называются объекты, в которых коэффициенты подобия длин,

площадей и объемов постоянны для всех элементов объекта.

Кинематически подобными называются геометрически подобные объекты, сохраняющие при своем движении постоянным временной коэффициент подобия.

Динамическое подобие. При движении механических систем, куда относятся геологические структуры в дополнение к кинематической подобности модели и оригинала должно выполняться и их динамическое подобие.

Модель (m) и оригинал (o) называются динамически подобными, если они кинематически подобны и коэффициенты подобия сил Fr , ответственных за динамические процессы, в частности

Fmf равны между собой и постоянны во все рассматриваемые моменты времени для всех

Fof

течения оригинал и модель должны иметь одинаковое число Рейнольдса, которое равно

динамически подобных моделей равнозначно изучению динамики оригинала. Приведем перечень других коэффициентов подобия.

Таблица 2.2

240