
Кобрунов А_Мат методы модел в прикл геоф 2
.pdf


M x |
A x |
|
|
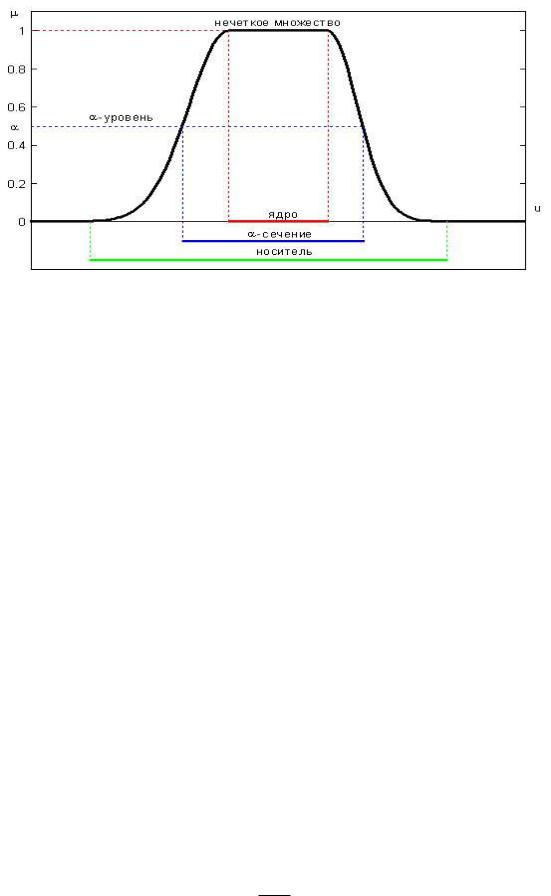
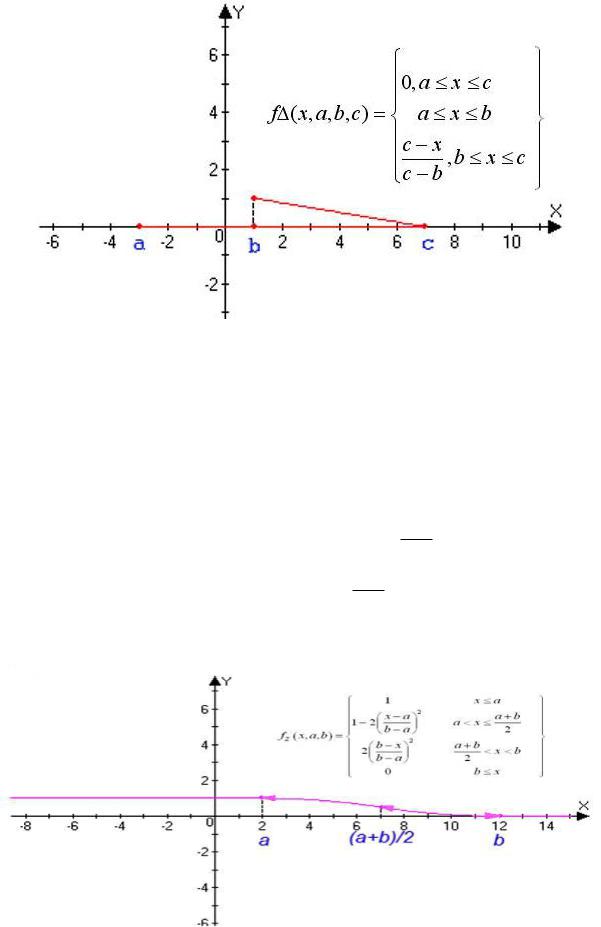
Рисунок 1.23 – Операции над нечеткие множествами
Эквивалентное обозначение таково: S x A x M x . Это обозначение связано с использованием логического «И». Другим названием этой операции служит «конъюнкция» или
логическое умножение.
Объединением A M двух нечетких множеств A и M , заданных на одном и том же
универсуме, называется нечеткое множество S с функцией принадлежности
S x max A x , M x . Другим названием этой операции служит «дизъюнкция» или
логическое сложение.
Эквивалентное обозначение таково: S x A x M x . Это обозначение связано с
использованием логического «Или». |
|
|
Разностью A \ M двух нечетких множеств |
A и |
M , заданных на одном и том же |
универсуме, называется нечеткое множество |
S |
с функцией принадлежности |
S x A x M x , A x M x . . Разность называют также дополнением M до A .
Это некоммутативная операция ( A \ M M \ A ).
Симметрической разностью A M двух нечетких множеств A и M заданных на одном и том же универсуме называется нечеткое множество S = A M с функцией принадлежности S x A x M x . Симметрическая разность удовлетворяет равенству:
AM A \ M M \ A , что собственно и определило название симметрическая.
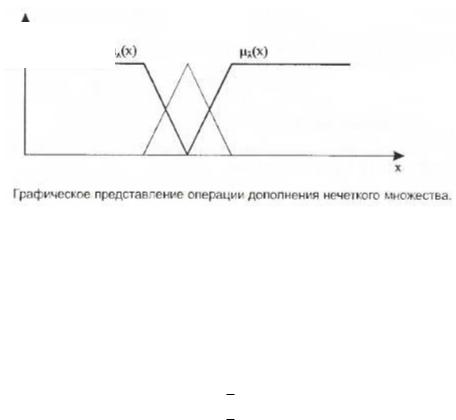
Дополнение A нечеткого множества A называется нечеткое множество с функцией принадлежности A x 1 A x . Это унитарная операция, для ее определения не требуется определение двух нечетких множеств.
187

 x
x 