Кобрунов А_Мат методы модел в прикл геоф 2

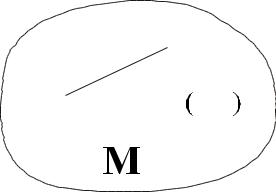
множестве сильно выпуклая функция достигает единственного минимума. Здесь сразу два

– квадратичен – например, имеет вид (1.2.3), задача (1.2.2) называется задачей квадратичного программирования. Квадратичный функционал сильно выпуклый и, поэтому, задача квадратичного программирования одновременно есть и задача выпуклого программирования,

внутренней стороной выпуклого многогранника в фазовом пространстве параметров m

образованного линейными уравнениями как уравнениями граней. Эти задачи называются задачами линейного программирования и допускают применение еще более специализированных алгоритмов. Последние основаны на том хорошо известном обстоятельстве,

что минимум (также как и максимум) линейной функции на выпуклом многограннике достигается

ввершинах многогранника.

Вформе (1.2.2) может быть записана и задача, в которой множество M образовано набором допустимых траекторий, каждая из которых характеризует параметрами образующими

91

элемент m . В этом случае задание множества M состоит в задании динамических уравнений для допустимых траекторий, а роль параметров y y j , j 1, L играют некоторые краевые или

начальные условия для этих траекторий. Такой класс задач называется задачами динамического программирования и весьма распространен при обработке геофизических данных – автоматизированная корреляция временных разрезов или корреляция разрезов скважин. Роль множества M , в частности играют всевозможные траектории осей синхфазности для временного разреза проходящих через заданные реперные точки. m – это конкретная траектория луча и y y j , j 1, L обязательные значения реперов для допустимой траектории.

Методы решения задач оптимизации подразделяются на аналитические и численные.

Аналитические методы основаны на изучении и решении уравнений, которым должен удовлетворять оптимальный элемент – решение задачи (1.2.5). Они в целом основаны на идее, в

соответствии с которой в точке минимума (экстремума), функция имеет обращающуюся в ноль производную. А также идеям родственным с этой, состоящей в свойствах проекций элемента на выпуклое множество. Развитие этих идеи на бесконечномерный случай и распространение на случаи задач с различными важными в приложениях особенностями компонент задачи

оптимизации. Эти методы чрезвычайно важны даже не в связи с тем, что позволяют найти конкретный оптимальный элемент, а прежде всего тем, что позволяют построить уравнения для выполнения последующего моделирования.

Численные методы оптимизации это большое разнообразие процедур, позволяющих шаг за шагом приблизиться к решению задачи оптимизации. Они имеют различную степень обоснования. От строго обоснованных и, представляющих, по сути, приемы численного решения и реализации тех требований, которые вытекают из аналитических методов поиска оптимальных элементов, до эвристических, не имеющих строгого обоснования своей ходимости. К числу последних относятся, например, так называемые генетические алгоритмы оптимизации. В

настоящее время количество модификаций численных методов оптимизации огромно. Оно даже не поддается обзору, поскольку основано на весьма большом числе разнородных идей и принципов. В этой связи, касаясь численных методов, следует уяснить лишь некоторые из основополагающих принципов. Что же касается конкретных реализаций, приспособленных к большому числу разнообразных конкретных ситуаций то современные общедоступные пакеты программ, такие как MathCad, Matlab, Maple, Mathematica и др. содержат их программную реализацию с весьма подробным описанием в соответствующих “Help”ах. Настоятельно рекомендую познакомиться с некоторыми из этих пакетов. Затраченное время будет оправдано.

92

1.2.2 Аналитические методы оптимизации

Рассмотрим один достаточно простой пример, демонстрирующий дух и принципы

получения уравнений, которым удовлетворяют оптимальные элементы.

Пусть в качестве множества M выступает множество функций f (x, y) двух переменных x и y , определенных в некоторой области S плоскости X 0Y и имеющие непрерывные частные

производные до второго порядка включительно. Элементами m M служат конкретные

Здесь fx (x, y), f y (x, y) обозначают, соответственно производные функции f (x, y) по х и у; L x, y, a,b,c – некоторая функция, в данном случае, пяти переменных x, y, a,b, c , в которую

вместо переменных a, b, c подставлены соответственно. Эта функция

в приложениях называется Лагранжевой плотностью. Задача оптимизации (1.2.5) состоит в нахождении такой функции f (x, y) , которая обеспечивает решение задачи:

L(x, y, a,b, c) достаточное число раз дифференцируема по всем своим переменным. Это значить,

что она дифференцируема ровно столько раз, какого порядка производные будут встречаться далее. Если (x, y) – произвольная непрерывно-дифференцируемая функция, заданная в S и

равная нулю на границе ∂S области S , то для любого числа t , f (x, y) t (x, y) уже не есть оптимальный элемент, но становиться таковым при t 0 . Тогда

12

J (t) L(x, y, f (x, y) t (x, y); fx (x, y) t (x, y); f y (x, y) t (x, y))dxdy,

S

рассматриваемая как обычная функция переменной t имеет экстремум при. t=0. Следовательно,

производная от J (t) должна обращаться в нуль при t=0:

12 Далее для краткости письма будем, где это не ведет к недоразумениям, опускать перечень переменных

(x, y) при функциях.

93

Второй интеграл, после применения формулы Грина, равен:

L fx dx L f y dy,

иобращается в нуль, поскольку значения (x, y, ) равны нулю на ∂S по условию. Тогда равенство:

считать, что на самом деле тождественным нулем является выражение в квадратных скобках последнего интеграла:

Это и есть искомое уравнение Эйлера, являющееся необходимым условием, которому удовлетворяет экстремаль (т.е. решение вариационной задачи) (1.2.4). Необходимые условия –

94

это те условия, которым должен удовлетворять оптимальный элемент. Но не факт что элемент им удовлетворяющий есть оптимальный. Решения уравнения (1.2.5) это «подозреваемые» на свойство оптимальности элементы. Из круга подозреваемых надо выбрать требуемый и доказать его оптимальность.

В том случае, когда на искомую экстремаль наложены дополнительные ограничения вида:

задача минимизации функционала (1.2.4) при условии (1.2.6) сводится к безусловной минимизации (т.е. минимизации рассмотренного выше вида) функционала:

Здесь i – числа, которые называются множители Лагранжа. Это правило – замена задачи на условный экстремум (1.2.6) задачей на безусловный экстремум (1.2.7) называется

«правило Лагранжа». Правда для того, чтобы применять это правило надо проверить выполнение

Gi x, y, f , fx , f y и регулярность их производной в окрестности искомого элемента. На самом

деле эти условия проверяются после того, как решение найдено и входят в перечень тех действий,

которые обосновывают применяемое правило – уравнения Эйлера. Числа i – находятся из условия, чтобы экстремаль (1.2.7) удовлетворяла системе уравнений (1.2.6).

В приведенном примере мы столкнулись с тем обстоятельством, что отображение

L x, y, f , fx , f y следовало дифференцировать по функциям, как по переменным. Таковы

производные Lf , Lfx , Lf y . Это характерное обстоятельство в задачах поиска оптимальных

функций. Эти производные следует рассматривать как производные Фреше от оператора,

определенного правилом L x, y, f , fx , f y . Напомним соответствующее определение (см. 1.1).

Если Х, Y – банаховы пространства, и – отображение (оператор) окрестности Q(f)

точки f D(A) X в Y , то A( f ) дифференцируемым по Фреше (сильно-дифференцируемым)

в точке f , если существует такой линейный непрерывный оператор, A ( f ) : X Y , зависящий от f и отображающий элементы h X в Y , что

95

называется непрерывно-дифференцируемым или отображением (оператором) класса C1 . Далее используется только сильная производная, поэтому термин «Фреше» зачастую опускается.

Благодаря понятию производной Фреше, оправдывается дифференцирование некоторого отображения по функции, как по переменной. Так собственно и вычисляются производные.

следовательно, во всех «точках» f x, y производная одна и та же. Следует всегда помнить, что

производная – это линейный оператор, действующий из Х в Y.

Следующая теорема называется правилом (принципом) Лагранжа и является основной в вариационном исчислении. Она является обобщением того приема, который был введен под тем же названием выше – переход от задачи (1.2.4, 1.2.6) к задаче на безусловный экстремум (1.2.7).

96

существование которого предполагается. Пусть Im A f Im A f . Тогда найдутся не равные

одновременно нулю элементы R1 и y* Y * , такие, что f x есть одновременно и решение задачи:

J f x A * f x y* h x 0

непрерывно-дифференцируемо и регулярно в точке f ( Im A f Y ), то 0 , и можно

считать, что 1.

Уравнение (1.2.8) называется уравнением Эйлера-Лагранжа. Это полный аналог и обобщение его частного случая (1.2.5), полученного для задачи (1.2.4). Более общепринято все уравнения, характеризующие необходимые условия экстремума, полученные вариационным путем называть уравнениями Эйлера.

Доказательство этого результата [см. А. Д. Иоффе, В. М. Тихомиров 34,, стр.87–88]. Здесь,

как и для уравнения (1.2.5), приведем лишь его упрощенную схему.

Пусть A( f ) y . Построим вариацию f (h,t) f x t h x r t такую, что

A( f (h,t)) y ,

lim r t 0.

t 0 t

97

Тогда:

A f (h,t) A f x t A' f x h x r 0 ,

где r – величина, связанная с r t и более высокого порядка малости, чем остальные члены.

Теперь рассмотрим функцию параметра t:

J f (h,t) min .

По условию ее минимум должен достигаться при t=0 и, следовательно, вычисляя

производную по t при t=0:

изометрического изоморфизма с некоторым элементом из Х*. Из последнего условия, по теореме

13 Оно введено на тот случай, если оператор А не регулярен. Тогда возникают особенности с применением теоремы о ядре. Равенство нулю этого числа делает весь результат тривиальным и справедливым для любого случая. Впрочем, в этом последнем случае он не только тривиален, но и бессодержателен с конструктивной точки зрения.

98

жестким и во многих интересных случаях не выполнено. И хотя, фактически, результат теоремы

факторизованного уравнения:

A' f x h x u ,

которая называется нормальной разрешимостью.

Последнее означает корректную разрешимость уравнения относительно фактор пространства Х по ядру оператора, или корректность решения задачи

A' f x h x u Y , h x X min . ,

В обратных геофизических задачах нормальная разрешимость чаще всего не имеет места.

Причина этого состоит в том, что не для всякой правой части уравнение A' f x h x u

вообще разрешимо. Но если решение существует, то существует и нормальное решение. Так,

например, приведенный выше результат, строго говоря, нельзя применять к модели обратной задачи гравиметрии:

состоящей в нахождении распределения плотности v в области V нижнего

полупространства по заданной функции u x0 , y0 на плоскости z 0 . Эта функция с точностью до постоянной (обратной гравитационной постоянной) есть вертикальная составляющая градиента потенциала гравитационного потенциала. Однако его неприменимость сводится лишь к тому, что строгое решение уравнения в (1.2.9) для всех u x0 , y0 Y может не существовать.

99

Упрощенно – не всякая функция из функционального пространства, например L2 , может рассматриваться как гравитационное поле некоторого распределения источников. Хотя приближенно и с очень высоким уровнем приближения (сколь угодно высоким) – можно. По этой причине нормальное решение существует с любой наперед заданной точностью и в этом отношении, учитывая реальное положение дел с точностью входных данных и конечной точностью счета, приведенный результат, оказывается, не просто применим к обратным задачам в форме типа (1.2.9), но и весьма конструктивным.

Приведенный выше результат – теорема Лагранжа (принцип Лагранжа) – это необходимые условия экстремума. Для его корректного применения следует еще доказать, что соответствующая конкретная задача имеет решение и записанные условия достаточны. Доказать это удается, как правило, лишь в весьма жестких предположениях относительно функционала

J( f x ) и оператора A f (x) . Оказывается, что для специальных случаев, к которым могут быть сведены многие задачи моделирования в науках о земле и, в частности, обратные геофизические задачи, соответствующие результаты можно доказать, исходя из других принципов, не используя операции дифференцирования и производных.

В большинстве рассматриваемых в приложениях случаях, функционал J( f x ) имеет специальный вид или может быть сведен к специальному виду – нормы в банаховом пространстве.

Рассмотрим следующую задачу, называемую задачей о наилучшем приближении. Далее мы несколько изменим обозначения, поскольку они носят более общий характер с точки зрения типа элементов подбираемых как оптимальные и линейного характера используемых операторов.

Пусть Х – банахово пространство, M – его подмножество и х0 – элемент из Х, не принадлежащий М.

•x0

M

X x

Рисунок 1.4 – Пояснение к обозначениям

Назовем элемент x наилучшим приближением к х0 (аппроксимацией х0) на множество М,

если

100