
Кобрунов А_Мат методы модел в прикл геоф 2
.pdf
|
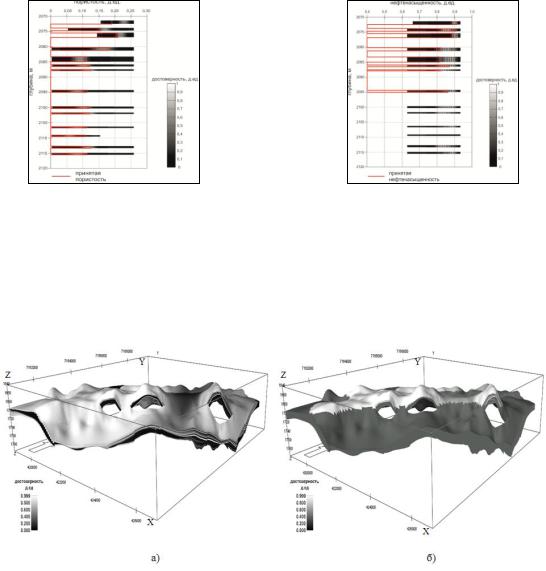
Рисунок 1.36 – Результаты расчёта |
Рисунок 1.37 – Результаты расчёта |
|
достоверности для кривой пористости в |
достоверности для кривой нефтенасыщенности |
||
|
скважине №114 |
в скважине №114 |
|
|
|
|
|
|
|
|
|
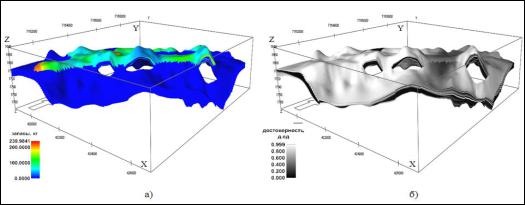
Рисунок 1.38 – Трёхмерные куб распределения достоверности подсчётных параметров (а – значение пористости, б – значение нефтенасыщенности)
Для оценки достоверности подсчёта запасов углеводородов предлагается воспользоваться свойством объединения нечётких множеств. При этом функция принадлежности находится как max{μ(y), μ(z)}
В результате может быть получена трёхмерная геолого-геофизическая модель распределения геологических запасов в объеме пласта, а также куб достоверности этих запасов, который отражает надёжность и объективность информации (рисунок 1.38). Этот куб следует использовать для дифференцированной оценки геологических запасов по достоверности, например в таблицы. Пример приведен ниже в таблице 1.3.
213
Глава 2. Физические основы
2.1 Фундаментальные законы классической механики
2.1.1 Введение
Для того, чтобы дать описание процессов движения объектов любой природы необходимо руководствоваться фундаментальными законами природы – законами сохранения. Эти законы устанавливают правила баланса количества для рассматриваемого объекта и являются первым шагом на пути построения его математической модели. Второй шаг это дополнение этого фундаментального закона эмпирическими закономерностями, позволяющими снизить до необходимого минимума число независимых переменных. Эти закономерности называются уравнениями состояния или материальными уравнениями.
2.1.2 Гидродинамическая модель пласта
Начнем с примера, относящегося к задачам гидрогеологии и демонстрирующим, как простые соображения о законе сохранения массы приводят к интересным уравнениям, служащим математическими моделями для целей добычи грунтовых вод.
Рассмотрим водоносный пласт [11], представляющий собой, например, пористый песчаник, залегающий на водонепроницаемом основании (иначе вода уйдет) и перекрытый толщей пород служащей покрышкой для гидродинамической системы. Вода находится в порах, а
процесс ее движения – это фильтрации воды сквозь поры. Следует заметить, что пористость рассматривается только открытая – т.е. та, которая обеспечивает каналы, по которым фильтрат движется. Закрытые поры – те, сквозь которые движение не передается, во внимание не принимаются. Также не принимаются во внимание и возможные эффекты превращения закрытых пор в открытые при некоторых перепадах давления.
Кроме того фильтруется однофазная жидкость – вода. В ней нет примесей (например, нефти),
которые имеют отличные от воды гидродинамические параметры и, которые могли бы отфильтровываться, усложняя картину движения. Основные величины, участвующие в формировании модели приведены на рис. 2.2. Пласт считается тонким относительно своих горизонтальных размеров, поэтому движением воды вдоль вертикальной координаты 0Z можно пренебречь. Используются прямоугольные декартовы координаты XYZ . Выделим элементарную призму, имеющую грани S1 и S2 соответственно со сторонами dx
Движение происходит, во-первых, в направлении оси 0X со скоростью vx
215




























