Кобрунов А_Мат методы модел в прикл геоф 2

yM E(x, Wm (m 1 M )) .

Сформулированная в начале раздела теорема утверждает, что уже двухслойная сеть с одним скрытым слоем является универсальным способом аппроксимации произвольной гладкой

зависимости. Процесс нахождения коэффициентов матриц Wm называется процессом обучения сети. Обучение осуществляется так, чтобы заданной последовательности входов соответствовала заданная система выходов y yi . {xi , yi } – обучающее множество. Такое обучение обеспечивает в последующий прогноз значений y yi по данным x xi в

других, отличающихся от обучающего множества случаях. Для обучения используются методы оптимизации, которые состоят в нахождении всех Wm из условия:

(1.2.48)

Для решения этой задачи существует целый ряд методов, таких как метод Голуба-Перейры

[3]. Основным способом нахождения коэффициентов, характеризующих действие нейронной сети является градиентный метод решения оптимизационной задачи (1.2.48). Он состоит в нахождении градиента (1.2.48) по параметрам wj m,i с последующим приравниваем результата нулю, что дает уравнения нахождения значений этих коэффициентов. Нахождение этих градиентов требует вычисления значения производной от сложной функции и приводит к рекуррентной процедуре,

которая называется процедурой обратного распространения ошибки. Она реализована во всех действующих нейронных сетях и служит основой для оптимального вычисления градиентов.

После того, как обучение завершено на обучающей выборке и точность проверена на контрольной последовательности, построенный алгоритм используется для прогнозирования значений изучаемого явления в недоступных для измерения выходных параметров.

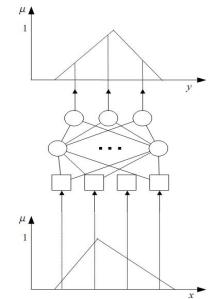
Использование нейронных сетей допускает комбинирование с методами нечеткой логики.

Такое расширение нейронно-сетевого подхода может быть реализовано в трех направлениях:

1.Вместо обычных чисел рассматривать нечеткие;

2.Использовать нейронные сети для представления нечетких правил;

3.Использование идей нейронных сетей (вычислений с использованием нейронных сетей)

для настройки параметров нечеткой системы.

Рассмотрим вкратце каждую из возможностей.

Нечеткие нейронные сети используют в качестве входных данных и весовых

коэффициентов вместо обычных – нечеткие числа. Арифметические операции и функция активации f определяются с помощью принципа обобщения. Собственно определить

131

следует сложение, умножение и монотонно возрастающую функцию активации от нечетких

чисел. Для определенности будем считать, что используемые нечеткие числа имеют треугольную форму. Это значить, что нечеткое число A имеет функцию принадлежности x треугольного

типа, характеризующуюся своей модой m , левой гранью ограничивающей носитель A слева – l

и правой границей, ограничивающей носитель справа – r . Сама же функция принадлежности имеет вид треугольника построенного по этим трем точкам. Обобщением значения функции

числами по этому принципу, являются универсальными аппроксиматорами только для нечетких непрерывных монотонных функций. Это значить, в частности, что они способны аппроксимировать лишь функции, у которых все входные и выходные значения только не положительны или только неотрицательны.

Использование нейронной сети для представления нечетких правил. Пусть нечеткая

дискретное разбиение этих носителей на интервалы

Вычисления с использованием нечетких правил с настройкой параметров нечеткой

системы с использованием нейронных систем. Это гибридные нейро-нечеткие системы, в

132

которых используется система нечетких правил с настройкой функции принадлежности для входных и выходных данных обучающего множества методами нейросетевых технологий.

Существует несколько архитектур гибридных систем, каждая из которых предназначена для решения своего круга задач.

Рассмотрим для примера нечеткую систему с двумя правилами и двумя переменными.

Правило 1 R1 ;если x1 есть A11 и x2 есть A11 , то y c11 x1 c12 x2 . Правило 2 R2 ;если x1 есть A21 и x2 есть A22 , то y c21 x1 c22 x2 .

Выход системы находится как линейная комбинация выходов каждого изб правил:

y 1 x1 2 x2 .

Можно представить следующую пятислойную нейронную сеть.

Слой 1. Выходными значениями этого слоя служат степени принадлежности входных значений нечетким множествам Aij x . Функция принадлежности может быть выбрана Гауссова типа:

где коэффициенты aij и bij должны быть подобраны в процессе обучения.

Слой 2. Вычисление уровня истинности правила Ri : i Ai1 xi Ai 2 x2 .

Слой 4. Расчет достоверности выходных правил: yi i ci1 x1 ci 2 x2 .

Слой 5. Суммирование выходов как нечетких чисел.

1.3 Векторы, тензоры и дифференциальные формы

1.3.1 Алгебра тензоров

Особенность задач моделирования в науках о земле, в отличие от более общих математических задач, включая задачи вычислительной математики, является то, что сценой, на которой развиваются моделируемые явления, служит трехмерное векторное пространство,

характеризующееся своими точками – элементами трехмерного пространства, радиус векторами,

133

которые обозначаем r {x1 , x2 , x3 }. И все это происходит в движении по временной координате

подразумевая, что он пробегает значения 1, 2, 3 и греческим, например нумерующим четверку координат {x0 , x1 , x2 , x3 }, =0, 1, 2, 3.

Величины xi это координаты радиус вектора r в базисе

i 1..3

Правило суммирования Эйнштейна состоит в том, что по дважды повторяющимся

Тогда в новой системе координат e e1 , e 2 , e 3 радиус вектор r имеет вид:

координаты в новом базисе вычисляются по формуле:

с помощью матрицы A 1 , обратной к той, с помощью которой осуществлялся переход от старого базиса e e1 ,e 2 ,e3 к новому e e1 , e2 , e3 , т.е. A aij . Ситуацию можно обобщить, и это

обобщение полезно, если считать, что переход от координат xi к координатам x i осуществляется с помощью функций x i x i x1 , x2 , x3 . Тогда в линейном приближении, исключая сдвиги,

134

используем как эквивалентные. Преобразования (1.3.5) и (1.3.6) называются соответственно

контрвариантным и ковариантным преобразованием. Таким образом, элементы базиса преобразуются с помощью преобразования а координаты с помощью ему обратного. Можно рассуждать и наоборот, принимая за исходное преобразование координат, и тогда элементы базиса преобразуются обратным образом. Поэтому принято называть один класс объектов,

которые преобразуются в одну сторону – ко-объектами или ковариантными, а другой класс объектов, которые преобразуются противоположным образом – контр объектами или контрвариантными объектами. Одни из них, скажем ковариантные, преобразующиеся так как преобразуются базисные элементы будем именовать нижними индексами. Другие,

преобразующиеся обратным законом, так, как преобразуются координаты вектора при преобразовании базиса – контрвариантные будем именовать верхними индексами. Ничего существенного не изменилось бы, если бы приняли наоборот – ковариантные = те что преобразуются по правилу верхних индексов, контрвариантные – по правилу нижних. Однако выбрав одно правило будем придерживаться его и в дальнейшем. Примером ковариантного вектора, служит градиент функции в прямоугольной декартовой системе координат:

Обратим внимание на использование обозначения операции дифференцирования скалярной функции – запятая и индекс переменной, по которой осуществляется дифференцирование. Такое обозначение подчеркивает ковариантный характер градиента и

135

сохраняет баланс верхних и нижних индексов в выражениях, в которых участвует операция дифференцирования.

Следующее замечание относится к частному случаю преобразований ортогональных

декартовых координат, осуществляемых с помощью матрицы A . Если компоненты вектора r

преобразуется с помощью матрицы A то длинна этого вектора в старых и новых координатах должна сохраняться. Это означает, что скалярное произведение на себя самого вектора и его

длинны – это преобразование ортогональных систем координат, реализуемое матрицей,

транспонированная к которой равна обратной. Такая матрица называется ортогональной (или унитарной в более общем случае).

Подобно тому, как вектор и ковектор – это одноиндексные объекты с верхним или

верхних и каким-то числом нижних индексов. Если по каждому из нижних индексов, число которых n наш объект преобразуется при преобразовании координат как ковектор, а по каждому

верхнему, число которых m как контр вектор (или просто вектор) то этот объект называется

тензором ранга M где M m n , n раз ковариантным и m раз контрвариантным. Важно еще задать и последовательность, в которой тензор преобразуется по своим индексированным компонентам, поскольку преобразование сначала по первому потом по второму это не то же самое что преобразование сначала по второму а затем по первому. Поэтому чтобы было совсем правильно, пишут так:

девятикомпонентные объекты с двумя индексами, именующими каждую из трех своих компонент.

В ортогональной декартовой системе координат отличие между контрвариантными и ковариантными индексами состоит лишь в том, что матрицы их преобразования сопряжены друг к другу. Поэтому в этом частном случае можно переводить ковариантные индексы в контрвариантные с заменой матрицы преобразования на ее транспонированную. Это означает,

суть ортогональные преобразования разница между контрвариантными и ковариантными индексами исчезает. Это обстоятельство позволяет для простоты записи «путать»

136

контрвариантные и ковариантные индексы. Однако этого следует избегать всякий раз, если за правильность записи не следует «платить слишком дорого». На самом деле выполнять координатные преобразования (1.3.5) и (1.3.6) в приложениях не часто встречающаяся задача.

Важно не столько вычислять, сколько с помощью этих законов определять изучаемые объекты – тензора.

Простейшим примером, иллюстрирующем появление тензора второго ранга, служит вычисление градиента векторного поля f r { f 1 r , f 2 r , f 3 r }, который представляет

тензора напряжений, деформаций в механике сплошных сред и многие другие объекты в физике.

Получаются они, как правило, следующими рассуждениями, определяющими и их смысл.

Представим себе, что на элементарное тело приложена нагрузка – сила. Она характеризуется напряжениями, представляющими собой вектор силы, отнесенный к элементарной площадке, на которую эта сила действует. Тогда на каждой из площадок, характеризуемых своим вектором нормали будет свой наблюдаемый вектор напряжений. Таким образом, под действием исходной нагрузки – вектора силы среда переходит в напряженное состояние, характеризуемое тем, что для

каждого вектора нормали есть вектор напряжений. Следовательно, напряженное состояние

нормированной площадью площадки. Но таким объектом может быть только двухиндексный объект Ti j и t j Ti j ni , который называется тензором напряжений. Подобные рассуждения

можно провести для деформаций и, вообще говоря, любых откликах реальных сред. Элементы тензора Ti j можно рассматривать как элементы матрицы, отображающий один вектор в

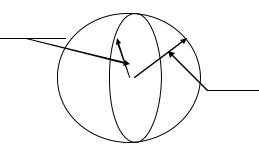
другой. В этом случае тензор можно графически представить себе как эллипс. Для этого

представим, что вектор r описывает единичную окружность с центром в начале координат. Тогда

образом, тензор можно рассматривать как аффинное преобразование – аффинор и обозначать его той же буквой T с элементами Ti j . Точнее аффинором называется линейное

преобразование A одного векторного пространства в другое обладающее свойством линейности и однородности:

137

A x x A x A x ; A x A x .

произвольное вещественное число.

t Tr

r

Рисунок 1.16 – Иллюстрация к понятию тензора

Подведем итог.

Для тензора второго ранга дважды контрвариантного имеем закон преобразования:

Для тензора второго ранга дважды ковариантного имеем закон преобразования:

Для тензора второго ранга ковариантного по одному и контрвариантного по другому индексу имеем закон преобразования:

Распространение этого правила на тензора более высоких чем два рангов представляется очевидным.

Если при перестановке контрвариантных или ковариантных индексов величина тензора не изменяется, то тензор называется симметричным по выбранной паре индексов. Если при той же операции он меняет знак на противоположный (например Tij Tji ) то тензор называется

антисимметричным.

Операции с тензорами.

138

это такой тензор, в котором при перестановке индексов компоненты меняют знак на противоположный: Cij C ji . Наиболее значимы двухиндексная и трехиндексная

альтернация. Двухиндексная альтернация тензора Aij состоит в построении тензора

Диагональные элементы кососимметричного тензора равны нулю а в силу антисимметрии существенное значение имеют лишь три его компоненты C12 ,C13 ,C23 . Аналогично можно выполнять двухиндексную альтернацию для тензора произвольного ранга более двух. Для

этого в тензоре Aijkl....m выбирается пара индексов, по которым будет проведена

альтернация, например второй и последний и, далее, строится кососимметрический по

состоящую в том, что в процессе трехиндексной альтернации четные перестановки индексов берутся с положительным знаком. Нечетные – с отрицательным. Кроме того единственная существенная компонента результата трехиндексной альтернации это

C123 .

Не всякий многоиндексный объект есть тензор. Тензор это специфичный класс многокомпонентных объектов подчиняющихся введенным законам преобразования при преобразовании координат. В этой связи представляется важным уметь определять – является ли тензором введенная многокомпонентная величина. Принципом такой проверки служит возможность получения инвариантов из заданной многокомпонентной величины и системы векторов или тензоров, о которых заведомо известен их векторный или тензорный характер.

Точнее справедливы такие результаты.

Признаки (необходимые и достаточные условия) тензоров.

1.Пусть Amnk трехиндексный объект и um , vn , wk контрвариантные и ковариантный вектор.

Тогда если Amnk um vn wk есть скаляр для любых um , vn , wk ,(сохраняющийся при любых координатных преобразованиях), то Amnk дважды ковариантный и единожды контрвариантный тензор третьего ранга.

140