
- •Введение
- •Памятка студенту
- •Тема 1: Аксиоматический метод
- •1.1 Сущность аксиоматического метода
- •1.2 Геометрия Евклида – первая естественно научная теория
- •1.3 Предмет математики
- •1.4 Место и роль математики в современном мире, мировой культуре и истории, в том числе в гуманитарных науках
- •Тема 2: Элементы теории множеств
- •2.1 Основные понятия теории множеств
- •2.2 Способы задания множеств
- •2.3 Операции над множествами
- •2.3.1 Пересечение множеств
- •2.3.2 Объединение множеств
- •2.3.3 Вычитание множеств
- •2.3.4 Дополнение
- •2.4 Формула Грассмана
- •Тема3: Элементы математической логики
- •3.1 Введение
- •3.2 Высказывания и операции над высказываниями
- •3.3 Формулы логики высказываний
- •Тема 4: Элементы комбинаторики
- •4.1 Введение
- •4.2 Простейшие комбинаторные задачи
- •4.3 Правила умножения и сложения
- •4.3 Выбор нескольких элементов. Размещения. Сочетания
- •Тема 5: Элементы теории вероятностей
- •5.1 Введение
- •5.2 Случайные события и их вероятности
- •1) Найти число n всех возможных исходов данного опыта;
- •2) Принять предположение о равновероятности (равновозможности) всех этих исходов;
- •3) Найти количество n(а) тех исходов опыта, в которых наступает событие а;
- •4) Найти частное , оно и будет равно вероятности событияА.
- •5.3 Операции с вероятностями
- •Если а и в несовместны, то
- •Тема 6: Элементы математической статистики
- •6.1 Случайные величины
- •6.2 Основные понятия математической статистики
- •6.3 Характеристики и параметры статистической совокупности
- •6.4 Статистика – дизайн информации
- •6.4.1 Группировка информации в виде таблиц
- •6.4.2 Графическое представление информации
- •6.4.3 Гистограммы распределения большого объема информации
- •6.5 Числовые характеристики или «паспорт» выборки
- •1) Сложить все результаты, входящие в эту выборку;
- •2) Полученную сумму разделить на количество всех результатов.
- •1) Каждую варианту умножить на ее кратность;
- •2) Сложить все полученные произведения;
- •3) Поделить найденную сумму на сумму всех кратностей.
- •1) Каждую варианту умножить на ее частоту;
- •2) Сложить все полученные произведения.
- •6.6 Экспериментальные данные и вероятности событий
- •Тема 7: Элементы математического моделирования
- •7.1 Два подхода к построению моделей
- •7.2 Три типа моделей
- •7.3 Что такое математическое моделирование?
- •7.4 Основные этапы математического моделирования
- •7.5 Классификация моделей
- •7.6 Примеры математических моделей
- •1) Задача о движении снаряда.
- •2) Задача о баке с наименьшей площадью поверхности.
- •3) Транспортная задача.
- •4) Задача о радиоактивном распаде.
- •5) Задача о коммивояжере.
- •1. Построение модели.
- •6) Задача о нахождении связи между структурой и свойствами веществ.
- •7) Задача об определении надежности электрической цепи.
- •8) Задача о диете.
- •7.7 Выводы
- •Тема 8: Элементы истории математики
- •Вавилония и Египет Вавилония
- •Греческая математика Классическая Греция
- •Александрийский период
- •Упадок Греции
- •Индия и арабы
- •Средние века и Возрождение Средневековая Европа
- •Возрождение
- •Начало современной математики
- •Достижения в алгебре
- •Аналитическая геометрия
- •Математический анализ
- •Современная математика
- •Неевклидова геометрия
- •Математическая строгость
- •Задачи для самостоятельного решения
- •Тема 2: Элементы теории множеств Основной уровень
- •Повышенный уровень
- •Тема 3: Элементы математической логики Основной уровень
- •Повышенный уровень
- •Тема 4: Элементы комбинаторики Основной уровень
- •Повышенный уровень
- •Тема 5: Элементы теории вероятностей Основной уровень
- •Повышенный уровень
- •Тема 6: Элементы математической статистики Основной уровень
- •Повышенный уровень
- •Тема 1: Аксиоматический метод
- •Тема 7: Элементы математического моделирования
- •Тема 8: Элементы истории математики
- •Вопросы к экзамену (зачету)
2.3.4 Дополнение
В случаях, когда одно из множеств является подмножеством другого, А \ В называют дополнением множества В до множества А, и обозначают символом В'А
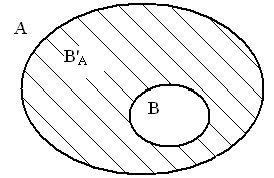
Пусть
В
![]() А.
Дополнением
множества
В
до множества А
называется множество, содержащее все
элементы множества А,
которые не принадлежат множеству В.
В
А.
Дополнением
множества
В
до множества А
называется множество, содержащее все
элементы множества А,
которые не принадлежат множеству В.
В
![]() А,
А
\ В
= В'А,
В'А
= {х|
х
А,
А
\ В
= В'А,
В'А
= {х|
х
![]() А
и х
А
и х
![]() В}.
В}.
Часто ограничиваются рассмотрением всевозможных подмножеств одного и того же множества, которое в этом случае называют основным или универсальным множеством. Обозначим основное множество буквой E. Для любого множества А, принадлежащего основному множеству Е, справедливы равенства: А U Е = Е, А ∩ Е = А.
Множество элементов основного множества Е, не принадлежащих множеству А, называется дополнением множества А до множества Е или просто дополнением и обозначается А'.
О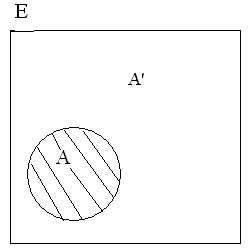 бъединение
множестваА
и его дополнения А'
есть основное множество: А
U А'
= E.
бъединение
множестваА
и его дополнения А'
есть основное множество: А
U А'
= E.
Пересечение множества со своим дополнением пусто: А ∩ А' = Ø.
Дополнение пустого множества есть основное множество: Ø' = E, а дополнение основного множества пусто: Е' = Ø.
На рисунке основное множество Е схематически изображено в виде прямоугольника, его подмножество А заштриховано, не заштриховано дополнение множества А'.
2.4 Формула Грассмана
Теория множеств используется при решении задач следующего вида:
В группе зверей 15 умных, 13 – красивых, и 8 мартышек. Сколько зверей в группе?
Решение:
Пусть
U
– множество умных зверей, К
– множество красивых. Тогда множество
мартышек будет обозначаться как
![]() ,
а множество всех зверей –
,
а множество всех зверей –![]() .
Значит, |U|
= 15, |K|
= 13 и
.
Значит, |U|
= 15, |K|
= 13 и
![]() =
8. Требуется найти
=
8. Требуется найти![]() .
Так как мартышки входят как в множество
умных, так и в множество красивых, то
при простом сложении элементов множеств,
мы мартышек посчитаем два раза. Тогда
из суммы элементов множеств умных и
красивых нужно одну часть мартышек
вычесть. Получим формулу:
.
Так как мартышки входят как в множество
умных, так и в множество красивых, то
при простом сложении элементов множеств,
мы мартышек посчитаем два раза. Тогда
из суммы элементов множеств умных и
красивых нужно одну часть мартышек
вычесть. Получим формулу:![]() .
Эта формула носит названиеформулы
Грассмана
для двух множеств. С помощью этой формулы
найдем количество зверей:
.
Эта формула носит названиеформулы
Грассмана
для двух множеств. С помощью этой формулы
найдем количество зверей:
![]() = 15 + 13 – 8 =
20.
= 15 + 13 – 8 =
20.
Пример 5. В классе 35 учеников. 20 человек посещают математический кружок, 11 – биологический. 10 человек не посещают кружков. Сколько биологов увлекается математикой?
Решение:
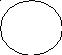
Изобразим ситуацию, изложенную в задаче, с помощью кругов Эйлера:
Т Е А В 

![]()
25 = 20 + 11 - |AB|. Выразим из этого уравнения |AB| и найдем, чему оно равно: |AB| = 20 + 11 – 25 = 31 – 25 = 6. Таким образом, 6 учеников увлекаются и биологией, и математикой.
Контрольные вопросы
Назовите основателя теории множеств.
Дайте определение множества, элемента множества.
Какие способы задания множеств вы знаете?
Какие множества называют равными?
Дайте определение подмножества. Чем отличаются собственные подмножества от несобственных?
Какие множества называются числовыми? Приведите примеры числовых множеств.
Пересечение, и объединение множеств. Примеры.
Вычитание и дополнение множеств. Примеры.
Какая из операций сильнее (выполняется раньше)?
Как изображаются операции над множествами с помощью диаграмм Эйлера-Венна?
Перечислите свойства операций над множествами.
Для решения каких задач используют формулу Грассмана?
