
- •Введение
- •Памятка студенту
- •Тема 1: Аксиоматический метод
- •1.1 Сущность аксиоматического метода
- •1.2 Геометрия Евклида – первая естественно научная теория
- •1.3 Предмет математики
- •1.4 Место и роль математики в современном мире, мировой культуре и истории, в том числе в гуманитарных науках
- •Тема 2: Элементы теории множеств
- •2.1 Основные понятия теории множеств
- •2.2 Способы задания множеств
- •2.3 Операции над множествами
- •2.3.1 Пересечение множеств
- •2.3.2 Объединение множеств
- •2.3.3 Вычитание множеств
- •2.3.4 Дополнение
- •2.4 Формула Грассмана
- •Тема3: Элементы математической логики
- •3.1 Введение
- •3.2 Высказывания и операции над высказываниями
- •3.3 Формулы логики высказываний
- •Тема 4: Элементы комбинаторики
- •4.1 Введение
- •4.2 Простейшие комбинаторные задачи
- •4.3 Правила умножения и сложения
- •4.3 Выбор нескольких элементов. Размещения. Сочетания
- •Тема 5: Элементы теории вероятностей
- •5.1 Введение
- •5.2 Случайные события и их вероятности
- •1) Найти число n всех возможных исходов данного опыта;
- •2) Принять предположение о равновероятности (равновозможности) всех этих исходов;
- •3) Найти количество n(а) тех исходов опыта, в которых наступает событие а;
- •4) Найти частное , оно и будет равно вероятности событияА.
- •5.3 Операции с вероятностями
- •Если а и в несовместны, то
- •Тема 6: Элементы математической статистики
- •6.1 Случайные величины
- •6.2 Основные понятия математической статистики
- •6.3 Характеристики и параметры статистической совокупности
- •6.4 Статистика – дизайн информации
- •6.4.1 Группировка информации в виде таблиц
- •6.4.2 Графическое представление информации
- •6.4.3 Гистограммы распределения большого объема информации
- •6.5 Числовые характеристики или «паспорт» выборки
- •1) Сложить все результаты, входящие в эту выборку;
- •2) Полученную сумму разделить на количество всех результатов.
- •1) Каждую варианту умножить на ее кратность;
- •2) Сложить все полученные произведения;
- •3) Поделить найденную сумму на сумму всех кратностей.
- •1) Каждую варианту умножить на ее частоту;
- •2) Сложить все полученные произведения.
- •6.6 Экспериментальные данные и вероятности событий
- •Тема 7: Элементы математического моделирования
- •7.1 Два подхода к построению моделей
- •7.2 Три типа моделей
- •7.3 Что такое математическое моделирование?
- •7.4 Основные этапы математического моделирования
- •7.5 Классификация моделей
- •7.6 Примеры математических моделей
- •1) Задача о движении снаряда.
- •2) Задача о баке с наименьшей площадью поверхности.
- •3) Транспортная задача.
- •4) Задача о радиоактивном распаде.
- •5) Задача о коммивояжере.
- •1. Построение модели.
- •6) Задача о нахождении связи между структурой и свойствами веществ.
- •7) Задача об определении надежности электрической цепи.
- •8) Задача о диете.
- •7.7 Выводы
- •Тема 8: Элементы истории математики
- •Вавилония и Египет Вавилония
- •Греческая математика Классическая Греция
- •Александрийский период
- •Упадок Греции
- •Индия и арабы
- •Средние века и Возрождение Средневековая Европа
- •Возрождение
- •Начало современной математики
- •Достижения в алгебре
- •Аналитическая геометрия
- •Математический анализ
- •Современная математика
- •Неевклидова геометрия
- •Математическая строгость
- •Задачи для самостоятельного решения
- •Тема 2: Элементы теории множеств Основной уровень
- •Повышенный уровень
- •Тема 3: Элементы математической логики Основной уровень
- •Повышенный уровень
- •Тема 4: Элементы комбинаторики Основной уровень
- •Повышенный уровень
- •Тема 5: Элементы теории вероятностей Основной уровень
- •Повышенный уровень
- •Тема 6: Элементы математической статистики Основной уровень
- •Повышенный уровень
- •Тема 1: Аксиоматический метод
- •Тема 7: Элементы математического моделирования
- •Тема 8: Элементы истории математики
- •Вопросы к экзамену (зачету)
4.2 Простейшие комбинаторные задачи
Знакомство с новыми понятиями начнем с двух простых задач.
Пример 1. Сколько четных двузначных чисел можно составить из цифр 0, 1, 2, 4, 5, 9?
Решение. Составим таблицу: слева от первого столбца поместим первые цифры искомых чисел, а выше первой строки – вторые цифры этих чисел. Так как в двузначном числе на первом месте может стоять любая цифра, кроме 0, то строки будут отмечены цифрами 1, 2, 4, 5, 9. Значит, в нашей таблице будет пять строк. На втором месте в искомом числе должна стоять четная цифра, значит, столбцы будут отмечены цифрами 0, 2, 4. Всего в таблице будет три столбца.
|
|
0 |
2 |
4 |
|
1 |
10 |
12 |
14 |
|
2 |
20 |
22 |
24 |
|
4 |
40 |
42 |
44 |
|
5 |
50 |
52 |
54 |
|
9 |
90 |
92 |
94 |
Клетки таблицы заполняются следующим образом: первая цифра числа равна метке строки, а вторая цифра – метке столбца, поэтому каждое из интересующих нас чисел попадет в определенную клетку таблицы. По строкам и столбцам мы перечислили все возможные варианты, значит, искомых чисел будет столько же, сколько клеток в таблице, т. е. 5 • 3 = 15.
Ответ: 15.
Здесь был осуществлен полный перебор всех возможных вариантов или, как обычно говорят в таких случаях, всех возможных комбинаций. Поэтому подобные задачи называют комбинаторными.
Пример 2. На завтрак Вова может выбрать плюшку, бутерброд, пряник или кекс, а запить их он может кофе, соком или кефиром. Из скольких вариантов завтрака Вова может выбирать?
Решение. Соберем все варианты в такой таблице: в ней три строки и четыре столбца, они образуют 12 клеток. Так как выбор еды и напитка происходит независимо, то в каждой клетке будет стоять один из возможных вариантов завтрака и, наоборот, любой вариант завтрака будет записан в одной из клеток. Значит, всего вариантов столько же, сколько клеток в таблице.
-
Плюшка
Бутерброд
Пряник
Кекс
Кофе
Кофе, плюшка
Кофе, бутерброд
Кофе, пряник
Кофе, кекс
Сок
Сок, плюшка
Сок, бутерброд
Сок, пряник
Сок, кекс
Кефир
Кефир, плюшка
Кефир, бутерброд
Кефир, пряник
Кефир, пряник
Ответ: 12.
Мы видим, что, хотя примеры 1 и 2 очень разные, их решения совершенно одинаковые. Основаны они на общем правиле умножения.
4.3 Правила умножения и сложения
Для того чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.
Правило умножения для двух независимых испытаний удобно объяснять, используя прямоугольники, разбитые на квадратики, или прямоугольные таблицы. Но если проводятся три испытания, то для иллюстрации надо использовать и длину, и ширину, и высоту, и на картинке получится прямоугольный параллелепипед, разбитый на кубики. Здесь уже рисунок и объяснения становятся сложнее, поскольку, например, будут невидимые кубики. Еще хуже дело обстоит с четырьмя испытаниями. В этом случае для рисунка нам просто не хватит измерений, ведь окружающее нас пространство всего лишь трехмерно.
Оказывается, правило умножения для трех, четырех и т. д. испытаний можно объяснить, не выходя за рамки плоскости, с помощью геометрической модели, которую называют деревом возможных вариантов. Она, во-первых, наглядна как всякая картинка, и, во-вторых, позволяет все учесть, ничего не пропустив.
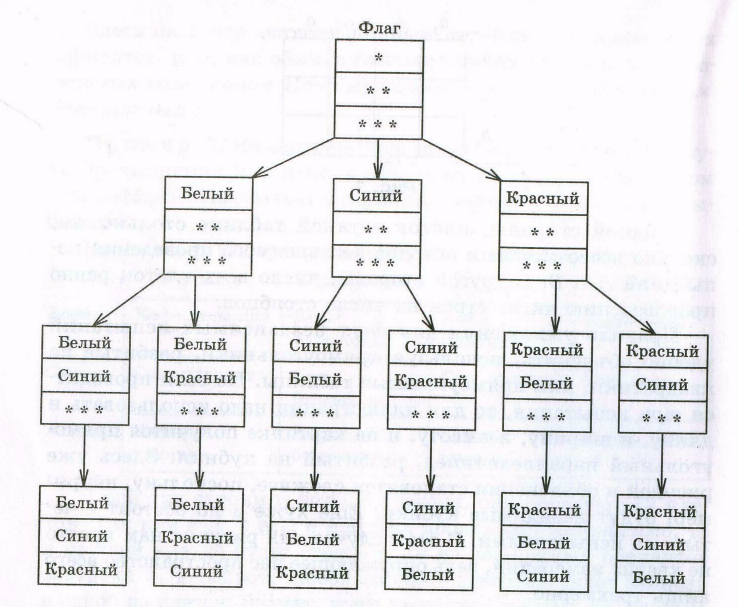 Пример
3. Несколько
стран в качестве символа своего
государства решили использовать флаг
в виде трех горизонтальных полос
одинаковых по ширине, но разных по цвету:
белый, синий, красный. Сколько стран
могут использовать такую символику при
условии, что у каждой страны свой,
отличный от других, флаг?
Пример
3. Несколько
стран в качестве символа своего
государства решили использовать флаг
в виде трех горизонтальных полос
одинаковых по ширине, но разных по цвету:
белый, синий, красный. Сколько стран
могут использовать такую символику при
условии, что у каждой страны свой,
отличный от других, флаг?
Решение. Будем искать решение с помощью дерева возможных вариантов (рис. 4.1). Посмотрим на его левую «веточку», идущую от «флага», пусть верхняя полоса – белого цвета, тогда средняя полоса может быть синей или красной, а нижняя – соответственно, красной или синей. Получилось два варианта цветов полос флага: белая, синяя, красная и белая, красная, синяя.
Пусть теперь верхняя полоса – синего цвета, это вторая «веточка».
Рисунок 4.1
Тогда средняя полоса может быть белой или красной, а нижняя – соответственно, красной или белой. Получилось еще два варианта цветов полос: синяя, белая, красная и синяя, красная, белая.
Аналогично рассматривается случай для верхней полосы красного цвета. Получится еще два варианта: красная, белая, синяя и красная, синяя, белая полосы флагов. Всего 6 комбинаций.
Ответ: 6.
Построенная схема действительно напоминает дерево, только перевернутое. Видимо, поэтому ее и называют деревом возможных вариантов.
Вот как, например, выглядит дерево возможных вариантов для примера 1 (рисунок 4.2):
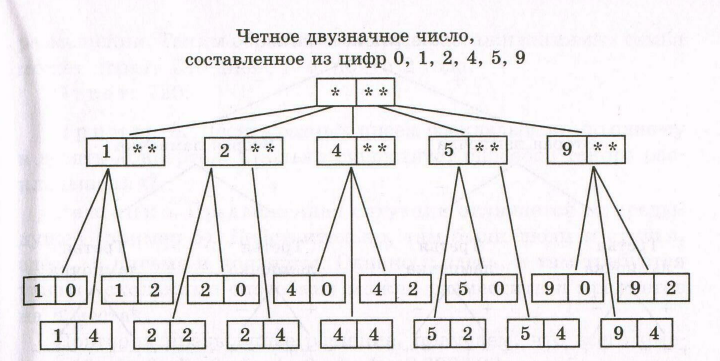 Для
следующего примера мы приведем три
различных способа решения: с помощью
простого перебора, с помощью дерева
вариантов и по правилу умножения.
Для
следующего примера мы приведем три
различных способа решения: с помощью
простого перебора, с помощью дерева
вариантов и по правилу умножения.
Рисунок 4.2
Пример 4. В коридоре висят три лампочки. Сколько имеется различных способов освещения коридора?
Решение.
Первый способ. Пронумеруем лампочки и будем писать «+» или «-» в зависимости от того, горит или не горит очередная лампочка. Тогда все способы освещения можно просто перечислить: + + +, + + -, + - +, - + +, + - -, - + -, - - +,
Всего 8 способов.
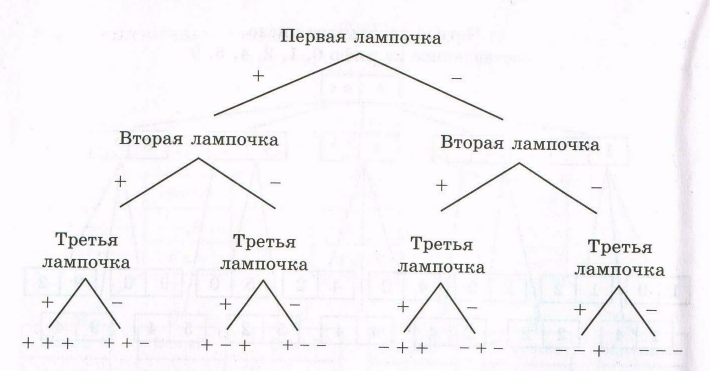 Второй
способ.
Дерево возможных
вариантов представлено на рисунке 4.3.
С его помощью находим, что осветить
коридор можно 8 способами.
Второй
способ.
Дерево возможных
вариантов представлено на рисунке 4.3.
С его помощью находим, что осветить
коридор можно 8 способами.
Третий способ. Первая лампочка может или гореть, или не гореть, т.е. имеется два возможных исхода. То же самое относится и ко второй, и к третьей лампочкам. Мы предполагаем, что лампочки горят или нет независимо друг от друга. По
Рисунок 4.3 правилу умножения получаем, что число всех способов освещения равно 2 • 2 • 2 = 8.
Ответ: 8.
У каждого из этих трех способов решения в каждом конкретном случае есть свои преимущества и свои недостатки. Выбор способа решения – за вами! Отметим все же, что правило умножения позволяет в один шаг решать самые разнообразные задачи. Например, оно приводит к крайне важному в математике понятию факториала. Рассмотрим сначала примеры.
Пример 5. В семье – 6 человек, и за столом в кухне стоят 6 стульев. В семье решили каждый вечер, ужиная, рассаживаться на эти 6 стульев по-новому. Сколько дней члены семьи смогут делать это без повторений?
Решение. Ответ оказывается неожиданно большим: почти два года! Объясним его. Для удобства рассуждений будем считать, что семья (бабушка, дедушка, мама, папа, дочь, сын) будет рассаживаться на стулья поочередно. Нас интересует, сколько всего существует различных способов их размещения на стульях.
Предположим, что первой усаживается бабушка. У нее имеется 6 вариантов выбора стула. Вторым садится дедушка и независимо выбирает стул из 5 оставшихся. Мама делает свой выбор третьей и выбор у нее будет из 4 стульев. У папы будет уже 3 варианта, у дочки – 2, ну а сын сядет на единственный незанятый стул. По правилу умножения получаем, что всего имеется 6·5·4·3·2·1 = 720 различных способов размещения. Таким образом, в «игру с рассаживаниями» семья может играть 720 дней, т. е. почти 2 года.
Ответ: 720.
Пример 6. Десять разных писем раскладывают по одному в десять конвертов. Сколько существует способов такого раскладывания?
Решение. Предложенная ситуация отличается от предыдущей (пример 5). Действительно, там были люди и стулья, здесь – письма и конверты. Однако и здесь, и там требуется узнать, сколькими способами можно разместить п предметов на п местах.
Повторяя предыдущее решение, получаем, что всего имеется 10·9·8·7·6·5·4·3·2·1=3 628 800 способов раскладывания писем по конвертам. Более 3,5 миллионов!
Ответ: 3628800.
Как мы видим, условия задач – разные, а решения, да и полученные ответы, по сути дела, одинаковы. Удобно поэтому ввести и одинаковые обозначения для таких ответов.
Определение. Произведение первых подряд идущих п натуральных чисел обозначают п!
п! = 1·2·3·…·(п-2)·(п-1)·п
Знак п! читается как «эн факториал», что в дословном переводе с английского языка означает «состоящий из п множителей». Приведем несколько первых значений для п:
1! = 1
2! = 1·2 = 2
3! = 1·2·3 = 6
4! = 1·2·3·4 = 24
5! = 1·2·3·4·5 = 120
6! = 1·2·3·4·5·6 = 720 и т.д.
Рассмотрим еще несколько примеров:
Пример
7. Вычислить:
а) 3!; б) 7!5!;
в)
![]() .
.
Решение. а) 3!=1∙2∙3=6.
б) т.к. 7!= 1∙2∙3∙4∙5∙6∙7 и 5!= 1∙2∙3∙4∙5, то 5! можно вынести за скобки, тогда получим 5!(6∙71)= 1∙2∙3∙4∙5∙41=4920.
в)
![]() .
.
Пример
8. Упростить
выражение:
![]() .
.
Решение.
![]() =1∙2∙3∙…∙(п
1)∙п∙(п+1), а
=1∙2∙3∙…∙(п
1)∙п∙(п+1), а
![]() =1∙2∙3∙…∙(п1),
после
сокращения получим п∙(п+1).
=1∙2∙3∙…∙(п1),
после
сокращения получим п∙(п+1).
Как же сформулировать общее утверждение, частными случаями которого являются решения примеров 3, 5 и 6? Вот один из возможных вариантов.
ТЕОРЕМА: п различным элементам можно присвоить номера от 1 до п ровно п! различными способами.
Каждый способ нумерации от 1 до п, о котором идет речь в теореме, часто называют перестановкой данного п-элементного множества. Действительно, можно считать, что каждая такая нумерация просто расставляет или переставляет все элементы множества в некотором порядке.
Перестановками из п элементов называют комбинации, которые отличаются друг от друга только порядком элементов.
Число перестановок множества из п элементов обозначают Рп. Значит, приведенную теорему можно записать в виде формулы:
Рп = п!
Кроме правила умножения в комбинаторике иногда используется еще правило сложения: Для того чтобы найти число всех возможных исходов независимого проведения одного из двух испытаний А или В, следует сложить число всех исходов испытания А и число всех исходов испытания В.
Пример 9. На столе в стаканчике стоит 5 карандашей и 3 ручки. Для того, чтобы написать записку (записать телефонный номер и т.п.), мы можем взять 1 из 5 карандашей или 1 из 3 ручек, то есть у нас имеется 5 возможностей выбора одного карандаша и 3 возможности выбора одной ручки. Так как мы выбираем только 1 предмет, карандаш или ручку, то число всех возможностей выбора равно: 5 + 3 = 8.
Правила умножения и сложения применимы для любого количества независимых испытаний.
Подведем итоги нашего знакомства с простейшими комбинаторными задачами. Мы получили основное правило – правило умножения, рассмотрели его геометрическую модель – дерево возможных вариантов, ввели новое понятие – факториал, сформулировали теорему о перестановках, в которой это понятие используется.
