Если а и в несовместны, то

Р(А + В) = Р(А) + Р(В).

Несовместность событий А и В удобно иллюстрировать следующим рисунком (рисунок 5.4). Если все исходы опыта – некоторое множество точек на рисунке, то события А и В – это некоторые подмножества данного множества. Несовместность А и В означает, что эти два подмножества не пересекаются между собой. Типичный пример несовместных событий – любое событие А и противоположное событие А.

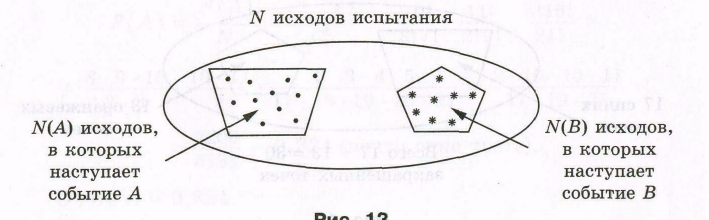
Рисунок 5.4

Разумеется, указанная теорема верна и для трех, и для четырех, и для любого конечного числа попарно несовместных событий. Вероятность суммы любого числа попарно несовместных событий равна сумме вероятностей этих событий.

Рисунок 5.5

Это важное утверждение как раз и соответствует способу решения задач «перебором случаев»:

Пример 8. В урне лежат 10 белых и 11 рыжих шаров. Случайным образом достают 5 шаров. Какова вероятность того, что среди этих шаров есть, по крайней мере, 4 белых шара?

Решение. Всего имеется N = исходов данного испытания. Обозначим буквойС интересующее нас событие. Тогда возможны два случая. Может случиться, что среди 5 выбранных шаров будет ровно 4 белых шара. Обозначим это событие буквой А. А может случиться, что все 5 выбранных шаров – белые, а рыжих нет вовсе. Обозначим это событие буквой В. Тогда А и В – несовместные события, в сумме дающие событие С. Значит, Р(С) = Р(А + В) = Р(А) + Р(В).

Вероятность события А считается так же, как и в примере 6:

.

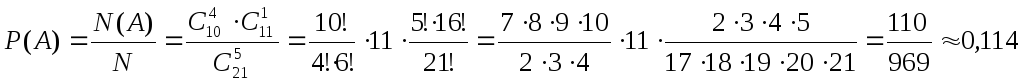Так же подсчитывается и вероятность события В.

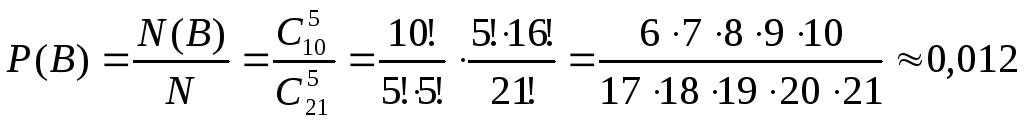
Значит, Р(С) = Р(А) + Р(В) = 0,114 + 0,012 = 0,126.

Ответ: ≈ 0,126.

Пример 9. В урне лежат 10 белых и 11 рыжих шаров. Случайным образом достают 5 шаров. Какова вероятность того, что среди этих 5 шаров есть, по крайней мере, 3 белых шара?

Решение. Пусть А – событие, состоящее в том, что среди выбранных пяти шаров есть роено 3 белых шара, В – событие, состоящее в том, что белых шаров роено 4, и С – событие, означающее, что все 5 выбранных шаров – белые. Тогда события А, В, С попарно несовместны, а нам требуется найти вероятность того, что произойдет или событие А, или событие В, или событие С. Вероятности каждого из этих событий в отдельности нами уже найдены (примеры 6 и 8). Значит, по теореме 2, Р(А + В + С) = Р(А) + Р(В) + Р(С) = 0,324 + 0,114 +…+ 0,012 = 0,45.

Ответ: = 0,45.

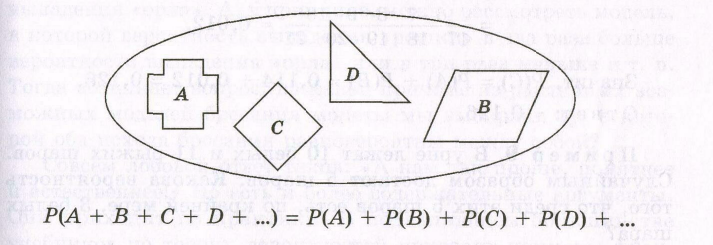
Мы видим, что и между событиями, происходящими в результате некоторого опыта, и между вероятностями этих событий могут быть какие-то соотношения, зависимости, связи и т. п. Например, события можно «складывать», а вероятность суммы несовместных событий равна сумме их вероятностей.

Произведением конечного числа событий называется событие, состоящее в том, что каждое из них произойдет.

Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность произведения этих событий.

Р(А+В)=Р(А)+Р(В)Р(АВ)

Пусть А и В – два случайных события одного и того же испытания. Тогда условной вероятностью события А или вероятностью события А при условии, что наступило событие В, называется число (при этом ВV). Обозначают Р(А/В).

Из этого определения следует, что Р(АВ)=Р(В)Р(А/В), т.е. вероятность произведения двух совместных событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло.

Пример 10. Из колоды в 36 карт поочередно достают две карты. Найти вероятность того, что вторым вынут червовый король, если первая карта – король черной масти.

Решение. Событие А состоит в одновременном наступлении двух совместных событий: А₂ – вынут король червей и А₁ – вынут король черной масти. При этом наступление события А₂ зависит от наступления события А₁. Найдем вероятности каждого из событий А₁ и А₂.

(т.к. в колоде всего 36 карт и мы берем 1 карту). N(A₁) = 2 (т.к. в колоде 2 короля черной масти). Тогда .

(т.к. мы одну карту из колоды вынули). N(A₂) = 1 (т.к. в колоде 1 король червей и мы вынули не его). Тогда .

Теперь найдем вероятность события А:

.

Событие А называется независимым от события В, если наступление события В не влияет на вероятность наступления события А.

ТЕОРЕМА 3: (теорема умножения вероятностей). Вероятность одновременного появления двух независимых событий равна произведению вероятностей этих событий.

Р(АВ)=Р(В)Р(А)

События А₁, А₂, …, А_п называются независимыми, если любые два из них попарно независимы и выполняется равенство Р(А₁А₂…А_п)= Р(А₁)Р(А₂)…Р(А_п).

Пример 11. В первой урне находятся 6 черных и 4 белых шара, во второй – 5 черных и 7 белых шаров. Из каждой урны извлекают по одному шару. Какова вероятность того, что оба шара окажутся белыми?

Решение. Пусть А₁ – из первой урны извлечен белый шар; А₂ – из второй урны также извлечен белый шар. Очевидно, что события А₁ и А₂ – независимы. Р(А₁)=,Р(А₂)=.

По теореме: Р(А₁А₂)=.

Пример 12. В экзаменационные билеты включено по два теоретических вопроса и по одной задаче. Всего составлено 28 билетов. Вычислить вероятность того, что, вынув наудачу билет, студент ответит на все вопросы, если он подготовил 50 теоретических вопросов и 22 задачи.

Решение. Полный ответ на билет состоит из произведения двух событий: студент одновременно ответит на два вопроса (событие А) и решит задачу (событие В).

Число всех возможных комбинаций из 56 вопросов по два составляет .

Так как студент подготовил только 50 вопросов, то число благоприятных исходов равно

. Р(А)=.

Вероятность события В определяется тем, что студент знает 22 задачи из 28 возможных Р(В) = .

Р(АВ)=Р(А)Р(В) = ∙=0,625.

В заключение обсудим следующий принципиальный вопрос: можно ли доказать, что вероятность выпадения «решки» при одном бросании монеты равна – .

Ответ отрицательный. Вообще говоря, сам вопрос не корректен, неясен точный смысл слова «доказать». Ведь доказываем мы что-либо всегда в рамках некоторой модели, в которой уже известны правила, законы, аксиомы, формулы, теоремы и т. п. Если речь идет о воображаемой, «идеальной» монете, то потому-то она и считается идеальной, что, по определению, вероятность выпадения «решки» равна вероятности выпадения «орла». А, в принципе, можно рассмотреть модель, в которой вероятность выпадения «решки» в два раза больше вероятности выпадения «орла» или в три раза меньше и т. п. Тогда возникает вопрос: по какой причине из различных возможных моделей бросания монеты мы выбираем ту, в которой оба исхода бросания равновероятны между собой?

Совсем лобовой ответ таков: «А нам так проще, понятнее и естественнее!» Но есть и более содержательные аргументы. Они приходят из практики. В подавляющем большинстве учебников по теории вероятностей приводят примеры французского естествоиспытателя Ж. Бюффона (XVIII в.) и английского математика-статистика К. Пирсона (конец XIX в.), которые бросали монету, соответственно, 4040 и 24000 раз и подсчитывали число выпадений «орла» или «решки». У них «решка» выпала, соответственно, 1992 и 11988 раз. Если посчитать частоту выпадения «решки», то получится у Бюффона иу Пирсона. Возникает естественноепредположение, что при неограниченном увеличении числа бросаний монеты частота выпадения «решки», как и частота выпадения «орла», все больше и больше будет приближаться к 0,5. Именно это предположение, основанное на практических данных, является основой нашего выбора в пользу модели с равновероятными исходами.

Кстати, вы вполне можете проверить это предположение даже на большем числе бросаний монеты. Например, если за один день каждый из 25 студентов вашей группы 40 раз бросит монету, то уже получится 1000 бросаний. За месяц «набежит» очень большое число.

Подведем итоги.

Основное понятие – вероятность случайного события, подсчет которой производится в рамках простейшей модели – классической вероятностной схемы. Важное значение и в теории, и в практике имеет понятие противоположного события и формула Р()= 1 - Р(А) для нахождения вероятности такого события.

Наконец, мы познакомились с несовместными событиями и с формулами Р(А + В) = Р(А) + Р(В), Р(А + В + С) = Р(А) + Р(В) + Р(С), позволяющими находить вероятности суммы таких событий.

Контрольные вопросы

1. Что называется испытанием?

2. Как называется результат испытания?

3. Какие виды событий бывают, чем они отличаются?

4. Что такое статистическая вероятность события?

5. Опишите классическую схему нахождения вероятности события.

6. Сформулируйте определение классической вероятности события.

7. Какие события называются противоположными?

8. Чему равна вероятность достоверного события, невозможного события?

9. Какие события называют несовместными?

10. Как можно найти вероятность одного из двух противоположных событий?

11. Какие события называются независимыми?

12. Сформулируйте теоремы сложения и умножения вероятностей.