6.5 Числовые характеристики или «паспорт» выборки

Вернемся к выборкам и рядам данных. У каждой выборки есть своего рода «паспортные данные», которые весьма существенны. Следует только точно понимать, что они в принципе не могут дать полной информации о выборке: абсолютно полной информацией о выборке является сама выборка. Но так как объемы выборок данных, как правило, очень велики, то приходится иметь дело с некоторым набором важных числовых характеристик этих выборок.

Итак, перейдем к составлению «паспорта» выборки. Нам поможет сделанный выше переход от выборок к полигонам частот выборок. Каждый полигон частот – это график некоторой функции. Этот график является ломаной из конечного числа звеньев. Вершины ломаной соответствуют вариантам и их частотам.

Рисунок 6.13

Размах выборки – это разница между наибольшей и наименьшей вариантой. На графике – это длина области определения полигона частот. Мода выборки – это наиболее часто встречающаяся ее варианта. На графике – это точка, в которой достигается максимум полигона частот (рис. 6.13). Если эта точка одна или если таких точек несколько, но подряд идущих, то выборку называют унимодальной (одна мода). Возможны и бимодальные (две моды) выборки и так далее.

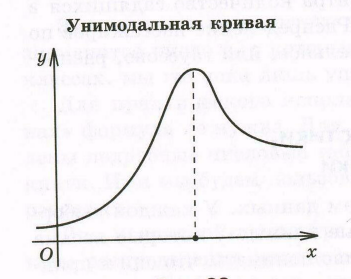
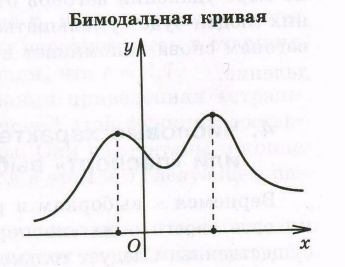
Рисунок 6.14

Наиболее важной характеристикой выборки является ее среднее значение или математическое ожидание описываемой случайной величины.

Для нахождения среднего значения выборки следует:

1) Сложить все результаты, входящие в эту выборку;

2) Полученную сумму разделить на количество всех результатов.

Например, пусть 10 студентов получили за тест по комбинаторике баллы

9, 14, 12, 9, 15, 12, 9, 15, 12, 12

из двадцати максимально возможных. Тогда среднее значение этой выборки результатов теста равно

Среднее значение выборки, к сожалению, не имеет наглядной иллюстрации с помощью полигона частот. Оно, по определению, усредняет все различные результаты, заменяя полную, но объемную информацию одним-единственным числом. Само это число, как мы видим, может и не входить в результаты выборки.

Среднее значение выборки можно вычислить, предварительно сгруппировав одинаковые слагаемые в числителе. Смотрите,

Такой способ подсчета очень удобно применять, когда выборка задана своей таблицей распределения вариант. В нашем примере вариант всего четыре штуки: 9, 12, 14, 15, а их кратности равны, соответственно, 3, 4, 1, 2. Значит, таблица распределения имеет такой вид:

Варианта	9	12	14	15
Кратность варианты	3	4	1	2

Поэтому можно было бы действовать и так. Сначала перемножить числа в каждом столбце этой таблицы. Потом сложить полученные произведения и затем найденную сумму разделить на 10. Сформулируем общее правило.

Для нахождения среднего значения выборки можно:

1) Каждую варианту умножить на ее кратность;

2) Сложить все полученные произведения;

3) Поделить найденную сумму на сумму всех кратностей.

В тех случаях, когда выборка задана распределением не кратностей, а распределением частот, удобно применять еще один способ подсчета среднего значения. Объясним его на том же примере.

Заметим, что 0,3 – это частота варианты 9; 0,4 – частота варианты 12; 0,1 – частота варианты 14; а последняя варианта 15 имеет частоту 0,2.

Варианта	9	12	14	15
Частота варианты	0,3	0,4	0,1	0,2

Значит, можно было бы просто перемножить числа в каждом столбце и затем сложить все полученные произведения. Сформулируем общее правило.

Для нахождения среднего значения выборки можно: