7) Задача об определении надежности электрической цепи.

Здесь мы рассмотрим пример вероятностной модели (основные понятия теории вероятностей находятся в теоретическом разделе 5 темы).

Предположим, что в электрическую цепь последовательно включены три элемента, работающие независимо друг от друга. Вероятности отказов 1-го, 2-го и 3-го элементов соответственно равны Р₁ = 0,1, Р₂ = 0,15, Р₃ = 0,2. Будем считать цепь надежной, если вероятность того, что в цепи не будет тока, не более 0,4. Требуется определить, является ли цепь надежной.

1. Построение модели. Так как элементы включены последовательно, то тока в цепи не будет, если откажет хотя бы один из элементов.

Пусть А – событие, состоящее в том, что тока в цепи не будет; событие А_i (i = 1, 2, 3) заключается в том, что i-тый элемент работает. Тогда Р(А₁) = 1 – 0,1 = 0,9, Р(А₂) = 1- 0,15 = 0,85, Р(А₃) = 1 – 0,2 = 0,8. Очевидно, что событие, состоящее в том, что по цепи проходит ток, равно событию, заключающемуся в том, что все три элемента работают, т.е. равно произведению трех независимых событий А₁, А₂ и А₃ (наступление каждого из этих событий не зависит от наступления двух других).

2. Решение математической задачи, к которой приводит модель. По теореме о вероятности произведения независимых событий Р(А₁А₂А₃) = Р(А₁)Р(А₂)Р(А₃) = 0,9·0,85 ·0,8 = 0,612. Тогда Р(А) + Р(А₁А₂А₃) = 1. Поэтому Р(А) = 1 – 0,612 = 0,388 < 0,4.

3. Интерпретация полученных следствий из математической модели. Р(А) = 0,388 < 0,4. Следовательно, цепь является надежной.

8) Задача о диете.

Дама просто приятная решила похудеть и, как это нередко случается, обратилась за советом к подруге. Подруга – дама приятная во всех отношениях, посоветовала ей перейти на рациональное питание, состоящее из двух новомодных продуктов Р и Q.

Дневное питание этими новинками должно давать не более 14 единиц жира (чтобы похудеть), но и не менее 300 калорий (чтобы не сойти с дистанции раньше). На банке с продуктом Р написано, что в одном килограмме этого продукта содержится 15 единиц жира и 150 калорий, а на банке с продуктом Q – 4 единицы жира и 200 калорий соответственно. При этом цена 1 кг продукта Р равна 15 у.е., а 1 кг продукта Q – 25 у.е.

Так как дама просто приятная в это время была несколько стеснена в средствах, то ее интересовал ответ на следующий вопрос: в какой пропорции нужно брать эти удивительные продукты Р и Q для того, чтобы выдержать условия диеты и истратить как можно меньше денег?

1. Построение модели. Обозначим через х количество продукта Р, а через у – количество продукта Q, требуемые для выполнения условий диеты.

Количество единиц жира, содержащегося в х кг продукта Р и в у кг продукта Q, равно 15х + 4у и по условию диеты не должно превосходить 14. Поэтому .

В свою очередь, количество калорий, содержащихся в х кг продукта Р и в у кг продукта Q, равно 150х + 200у и должно быть не меньше 300. Значит, .

Теперь о стоимости продуктов. Она равна z(х; у) = 15x + 25y и в соответствии с высказанными пожеланиями должна быть минимальной. Последнее записывается так: z(х; у) = 15x + 25y → min.

Итак, мы получили систему неравенств

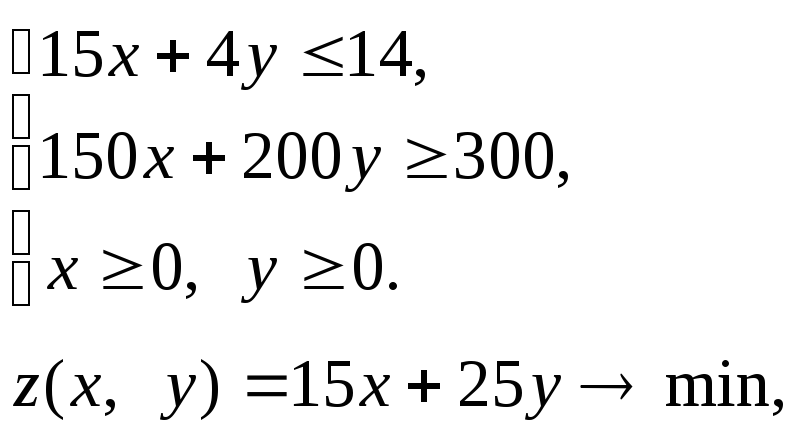
которая является математической моделью задачи.

Полученная система неравенств называется системой ограничений задачи, а функция z(х; у) называется целевой функцией задачи.

2. Решение математической задачи, к которой приводит модель. Для решения применим координатно-графический метод.

Решением системы ограничений является многоугольник, полученный путем пересечения областей решений всех неравенств системы. Решением линейного неравенства является одна из полуплоскостей, на которые прямая, соответствующая данному неравенству, делит координатную плоскость. Для определения искомой полуплоскости берется точка, не лежащая на прямой, ее координаты подставляются в неравенство. Если в результате получается верное числовое неравенство, то решением является полуплоскость, содержащая выбранную точку. В противном случае, решением является другая полуплоскость.

Введем на плоскости прямоугольную систему координат хОу и построим многоугольник решений системы ограничений нашей задачи.

Из условий х ≥ 0 и у ≥ 0 вытекает, что все точки, которые удовлетворяют системе ограничений, лежат в первой координатной четверти.

Теперь решим неравенство . Ему соответствует прямая, заданная уравнением, которая проходит через точкии. Для проверки возьмем точкуО(0; 0): 15 · 0 + 4 · 0 = 0 ≤ 14. Так как 0 ≤ 14 – верное неравенство, то решением неравенстваявляется полуплоскость, содержащая точкуО.

О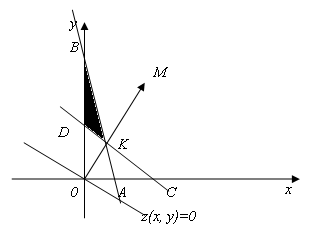бращаясь подобным же образом с неравенством, находим точки пересечения прямойс осями координат – точкиС(2; 0) и D(0; 1,5). Для проверки также возьмем точку О(0; 0): 150 · 0 + 200 · 0 = 0 ≥ 300. Так как 0 ≥ 300 – неверное числовое неравенство, то решением неравенства является полуплоскость, не содержащая точкуО.

Рисунок 7.4

Пересечением всех полуплоскостей является треугольник BDK (рис. 7.4). Точка К является точкой пересечения прямых АВ и CD и имеет координаты .

Теперь среди всех точек треугольника найдем ту, координаты которой удовлетворяют условию минимальности целевой функции z.

Для этого построим так называемую линию нулевого уровня функции z, которая задается уравнением z(x; y) = 0. Будем двигать эту прямую в направлении вектора , координатами которого являются соответствующие коэффициенты целевой функции, до места первой встречи этой прямой с треугольникомBDK. Искомой точкой будет точка К. То есть искомые значениях = , у = 1.

3. Интерпретация полученных следствий из математической модели. Таким образом, чтобы выполнить условия диеты и истратить при этом как можно меньше средств, продукты Р и Q нужно брать в отношении х : у = : 1 = 2 : 3. То есть на 2 части продукта Р брать 3 части продукта Q.